Exercises

1. Let \( f(x) = \dfrac{1}{x - 1} \) and \( g(x) = \dfrac{4 - 3x}{1 - x} \)
   1. Does \( \displaystyle \lim_{x \rightarrow 1} ~ f(x) \) exist? What about \( \displaystyle \lim_{x \rightarrow 1} ~ g(x) \)?
   2. Could you use the limit sum rule to find \( \displaystyle \lim_{x \rightarrow 1} ~ \left( f(x) + g(x) \right) \)?
   3. Does \( \displaystyle \lim_{x \rightarrow 1} ~ \left( f(x) + g(x) \right) \) exist?
2. Let \( f(x) = x^2 + 2x \) and \( g(x) = \dfrac{1}{x} \)
   1. Does \( \displaystyle \lim_{x \rightarrow 0} ~ f(x) \) exist? What about \( \displaystyle \lim_{x \rightarrow 0} ~ g(x) \)?
   2. Could you use the limit product rule to find \( \displaystyle \lim_{x \rightarrow 1} ~ \left( f(x)g(x) \right) \)?
   3. Does \( \displaystyle \lim_{x \rightarrow 0} ~  f(x)g(x)  \) exist?
3. The limit sum and limit product theorems have the form
   “If A, then B”
   where A and B are mathematical statements. The converse of such a theorem is
   “If B, then A”
   For example, the converse of the limit sum theorem is
   “If \( \displaystyle \lim_{x \rightarrow a} ~ \left( f(x) + g(x) \right) \) exists, then \( \displaystyle \lim_{x \rightarrow a} ~ f(x) \) exists and \( \displaystyle \lim_{x \rightarrow a} ~ g(x) \) exists”
   What do your results in part a) and part b) above tell you about the converses of the limit sum and limit product theorems?

1. What is the domain \( \mathcal{D} \) of the function \( g(x) = \dfrac{x - 3}{\sqrt{5x + 1} - \sqrt{3x + 7}} \)?
2. Determine \( \displaystyle \lim_{x \rightarrow 3} ~ g(x) \)

3. For what value of the constant \( k \) is the function

   \[ f(x) = \begin{cases} g(x), & \text{ if } x \in \mathcal{D} \\ k, & \text{ if } x = 3 \end{cases} \]

   continuous on its domain?

   Comment: The point \( x = 3 \) is called a removable discontinuity of \( g(x) \) since \( \displaystyle \lim_{x \rightarrow 3} ~ g(x) \) exists, allowing us to define the continuous function \( f(x) \).

1. A function \( g(x) \) is the ratio of two quadratic polynomials. The numerator is \( x^2 - 1 \), and it is known that the graph \( y = g(x) \) has a vertical asymptote at \( x = 2 \). It is also known that \( g \) has a removeable discontinuity at \( x = 1 \), and that \( \displaystyle \lim_{x \rightarrow 1} ~ g(x) = -2 \).
   1. Construct an equation for the function \( g(x) \) and evaluate \( \displaystyle \lim_{x \rightarrow \infty} ~ g(x) \).
   2. Sketch the graph of \( y = g(x) \).
2. Given the function \( f(x) = \dfrac{x^3 + ax^2 + bx + 5}{x^3 + 2x^2 - x - 2} \), determine whether there are numbers \( a \) and \( b \) such that both \( \displaystyle \lim_{x \rightarrow 1} ~ f(x) \) exists, and \( \displaystyle \lim_{x \rightarrow - 1} ~ f(x) \) exists. If so, evaluate both limits.

1. Evaluate \( \displaystyle \lim_{x\rightarrow a} \dfrac{x^3 - a^3}{x-a} \).
2. Now consider \( \displaystyle \lim_{x \rightarrow a} \dfrac{x^{\frac{1}{3}} - a^{\frac{1}{3}}}{x-a} \). Let \( u = x^{\frac{1}{3}} \), and \( b = a^{\frac{1}{3}} \), and hence transform this to a limit in \( u \) and \( b \) which you can evaluate. Express your answer in terms of \( a \).
3. Sketch a graph of the function \( y = f(x) = x^{\frac{1}{3}} \) and pick a point \( (x, x^{\frac{1}{3}}) \) on the graph for some \( x \gt 1 \), but near to \( 1 \). Suppose that \( a = 1 \) in part b). Hence interpret \( \displaystyle \lim_{x \rightarrow 1} ~ \dfrac{x^{\frac{1}{3}} - 1}{x-1} \) both geometrically, and as a rate of change.

Exploring a difference of infinities:

Consider the function \( f(x) = \sqrt{x^2 + 1} - x \).

1. Make an educated guess about the behaviour of \( f(x) \) as \( x \rightarrow \infty \) and as \( x \rightarrow - \infty \). Justify your reasoning.
2. Evaluate \(\displaystyle \lim_{x \rightarrow \infty} ~ f(x) \).

A trigonometric limit:

A surveyor takes sightings of the top, \( P \), of a tree, with elevations \( \theta, 2\theta \), and \( 3\theta \), as shown.

1. Use geometry and the sine law to show that\[ \frac{AB}{BC} = \frac{\sin{(3\theta)}}{\sin{(\theta)}} \]
2. Write \( \sin{(3\theta)} = \sin{(\theta + 2\theta)} \), and then use a trigonometric identity and limit laws to show that \( \displaystyle \lim_{\theta \rightarrow 0}~\frac{\sin{(3\theta)}}{\sin{(\theta)}} = 3 \)

1. Does \( \displaystyle \lim_{x \rightarrow 1} ~ f(x) \) exist? Explain your answer.
2. Is \( f \) continuous at \( x = 1 \)? Why, or why not?
3. Sketch the graph of \( f(x) \).

A surprising limit!

In the diagram, \( C_1 \) is a fixed circle \( (x-a)^2 + y^2 = a^2 \), of radius \( a \), and \( C_2 \) is a smaller circle \( x^2 + y^2 = u^2 \), with variable radius \( u \) such that \( 0 \lt u \lt a \). The point \( P \) is \( (0, u) \), and \( Q \) is the first quadrant intersection of \( C_1 \) and \( C_2 \). The line through \( P \) and \( Q \) meets the \( x \)-axis at \( R~(f(u), 0) \).

1. Show that, in terms of the variable \( u \) and the constant \( a \), \( f(u) = \dfrac{u^2}{2a-\sqrt{4a^2 -u^2}} \)
2. Hence evaluate \( \displaystyle \lim_{u \rightarrow 0} ~ f(u) \).

1. Suppose that the size of a population at time \( t\geq 0 \) is given by \( N(t)=\dfrac{at}{b+t} \), where \( a \) and \( b \) are positive constants.
   1. Determine the time \( t_h \) at which \( \,N(t_h ) = \frac{1}{2} a\, \).
   2. Given that \( \displaystyle \lim_{t \rightarrow \infty} ~ N(t) = 2.4 \times 10^4 \), find the value of \( a \). Hence interpret the role of the time \( t_h \) found in part i).
2. In a predator-prey interaction, the function \( g(x) = \dfrac{ax}{1+cx} \) represents the number of encounters of prey (\( x \)) per predator during the hunting period of the predators, where \( a \) and \( c \) are positive constants.
   1. What happens to the encounters per predator as the number of prey, \( x \), becomes very large (i.e. what is \( \displaystyle \lim_{x \rightarrow \infty} ~ g(x) \))?
   2. The constant \( c \) in this model is proportional to the time the predator spends eating each prey. What effect does an increase in \( c \) have on your answer in part i)? Explain why this is reasonable biologically.
3. The velocity \( v \) of a chemical reaction involving enzymes is described by the Michaelis-Menten equation, \( v = \dfrac{ax}{b+x} \), where \( x \) is the substrate concentration. In light of your results from part a), explain the roles of the positive constants \( a \) and \( b \) in this model.

1. Sketch the function \( H( t - \pi ) \) and show that \( \displaystyle \lim_{t \rightarrow \pi} ~ H(t - \pi) \) does not exist.
2. Write out a definition of the function \( g(t) = H(t) + H(t - \pi ) \). (It will have three ‘pieces’.)
3. Define the function \( f(t) = g(t)\cos{(t)} \), and sketch the graph of \( y = f(t) \) on the interval \( [-\pi,3\pi] \), indicating any points where \( f \) is discontinuous. Explain your reasoning using the definition of continuity.

A “functional” equation to solve:

A function \( f(x) \) satisfies the equation \( f(x) + xf(1 - x) = 1 + x^2 \).

1. Determine an explicit equation for \( f(x) \) in terms of \( x \).
2. Show that\[ \lim_{x \rightarrow \infty} ~ (f(x) - (2-x)) = 0 \] that is, that \( f(x) \) has an oblique asymptote \( y = 2 - x \) as \( x \rightarrow \infty \).

An interesting additional tool for evaluating limits:

Consider the limit \( \displaystyle \lim_{x \to 0} ~ \left\lvert x \right\rvert \sin{\left( \frac{\pi}{x} \right)} \). We cannot use the limit product rule to evaluate the limit since \( \displaystyle \lim_{x \to 0} ~ \sin{\left( \frac{\pi}{x} \right)} \) does not exist.

Looking at the plot of the function on the interval \( \left[ -\frac{3}{2}, \frac{3}{2} \right] \)

notice that the oscillations grow increasingly more crowded as \( x \) approaches \( 0 \).

Zooming in on \( x = 0 \) by decreasing the width of the interval to \( [-1, 1] \) gives: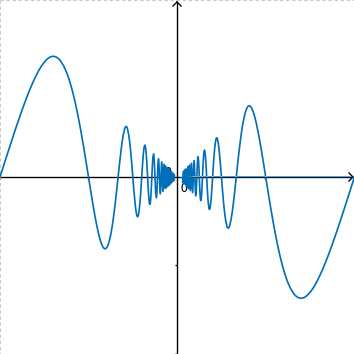

Decreasing the width of the interval to \( \left[ -\frac{1}{2}, \frac{1}{2} \right] \):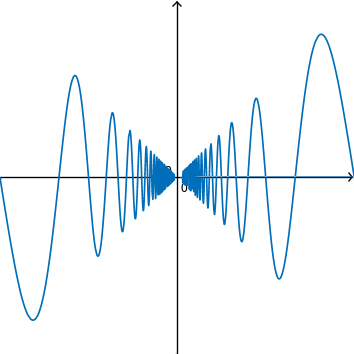

Decreasing the width of the interval to \( \left[ -\frac{1}{10}, \frac{1}{10} \right] \):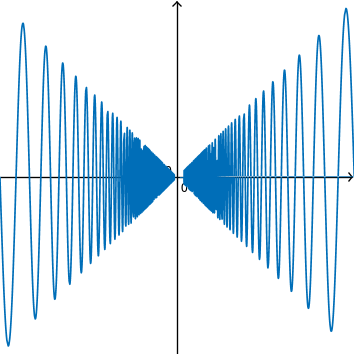

Observe that, no matter how small the viewing interval is, the function continues to oscillate extremely frequently as \( x \to \infty \). However, the amplitude of the oscillations appear to decrease linearly as \( x \to 0 \), as if the function values are bound, or “hemmed in” by lines of unit slope (observe that the amplitude approximately equals the magnitude of the \( x \) value, implying a slope of \( 1 \) on the bounding lines). This appears to force the limit to \( 0 \) as \( x \to 0 \).

This behaviour is made more apparent by combining the function with the apparent bounds \( \left\lvert x \right\rvert \) and \( -\left\lvert x \right\rvert \) on the intervals \( \left[ -1, 1 \right] \) (left) and \( \left[ -\frac{1}{10}, \frac{1}{10} \right] \) (right).

It is clear that the functions \( \left\lvert x \right\rvert \) and \( -\left\lvert x \right\rvert \) are acting to “funnel” the function \( \left\lvert x \right\rvert \sin{\left( \frac{\pi}{x} \right)} \) towards a limit of \( 0 \) as \( x \to 0 \). This is a result of the fact that the values of the sine function lie between \( 1 \) and \( -1 \) for any value of the argument; that is,

Thus, multiplying the inequality by \( \left\lvert x \right\rvert \) (which is non-negative), we see that

Since both of the “outer” functions \( \pm \left\lvert x \right\rvert \) approach \( 0 \) as \( x \to 0 \), so also does the “inner” function \( \left\lvert x \right\rvert \sin{\left( \frac{\pi}{x} \right)} \). Informally, the inner function gets “squeezed” or “sandwiched” between the two outer functions.

The above example illustrates the squeeze theorem, which essentially says that

1. Use the squeeze theorem to show that \( \displaystyle \lim_{x \rightarrow 0} ~ x^2 \cos \left(\frac{2}{x}\right) = 0 \).
2. The squeeze theorem can also be applied as \( x \rightarrow \infty \). Given that\[ \frac{3x-1}{x} \lt f(x) \lt 3 - \frac{1}{1+x^2} \text{for all } x \gt 10 \] what is \( \displaystyle \lim_{x \rightarrow \infty} ~ f(x) \)?