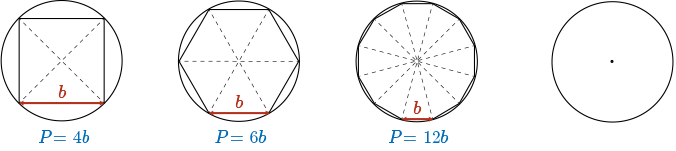
The Greek Method of Exhaustion (300-200 BC)

Greek mathematicians inscribed regular polygons within a circle.

They divided each \(n\)-sided polygon into \(n\) congruent triangles.

Each triangle has base, \(b\), and height, \(h\).

The area of each polygon can be found by multiplying the area of the triangles by \(n\).

The Greek Method of Exhaustion (300-200 BC)

As the number of sides in the polygon increases, the perimeter, \(P\), of each polygon approaches (becomes closer in value to) the circumference of the circle \((2\pi r)\).

The perimeter, \(P\), of each polygon is calculated by multiplying the the number of sides in the polygon, \(n\), by the length of the base of each triangle, \(b\).

\(P=nb\) \( \approx 2\pi r\)

The Greek Method of Exhaustion (300-200 BC)

Also, as the number of sides in the polygon increases, the height, \(h\), of each triangle approaches the length of the radius of the circle.

As the number of sides in the polygon increases, the area of the polygon approaches the area of the circle.