Hopefully, the graph that you sketched looked something like the following:
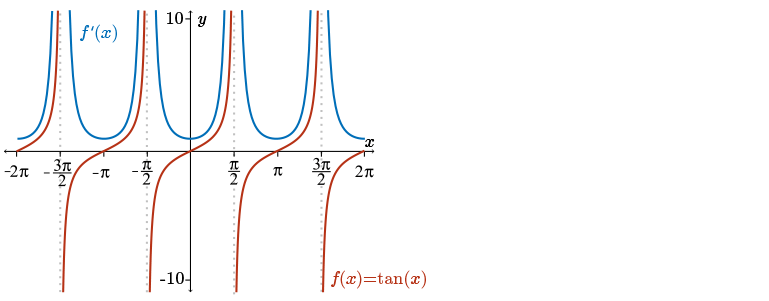
Does the shape of this curve appear similar to the shape of another trigonometric function?
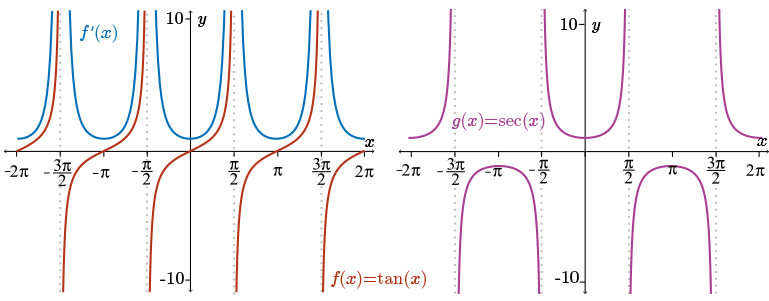
Consider the graph of the function \(g(x) = \sec(x)\).
The graph of \(g(x)\) and \(f'(x)\) share the same vertical asymptotes, but there are two observable differences in the graphs. The most obvious one is that the function \(g(x)\) takes on negative values, while \(f'(x)\) is always positive. What does this suggest? Absolute value of \(g(x)\)? The less obvious difference is that the the function \(f'(x)\) increases faster than the function \(g(x)\). This suggests that \(f'(x)\) is not the absolute value of \(g(x)\), but perhaps it is the square of \(g(x)\). From the graphical evidence, we suspect that \(f'(x) = (g(x))^{2} = \sec^{2}(x)\).