You begin a trip from home, point \( A \), travelling to point \( B \) and you are walking at a constant speed.

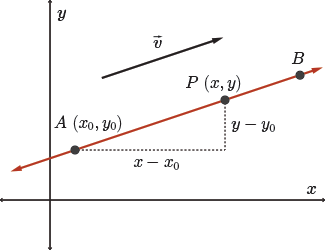
Your position, \( P \), relative to your initial position, \( A \, (x_0, y_0) \), changes over time, \( t \).

Specifically, the \( x \) and \( y \) coordinates of \( P \) depend on \( t \), the amount of time that has passed since you left home.

Your horizontal displacement at time \(t\) is \((x-x_0)\), while your vertical displacement is \((y-y_0)\).

Your velocity, \(\vec{v}\), can be described by the algebraic vector \( \vec{v}=(v_x, v_y) \), where \( v_x \) is the horizontal component of the velocity, and \( v_y \) is the vertical component.

Using this information, we can derive a relationship between the \( x \) and \( y \) coordinates and time, \( t \).

These two equations give the position, \( P\,(x, y) \), as a function of a single variable, \( t \).

The position of \(P\,(x,y)\) could be given by a linear function in the form \(y=mx+b\), but we have instead expressed both \(x\) and \(y\) in terms of a third variable, \(t\).

When we describe the relationship between two variables using a third variable, the third variable is called a parameter.

The equations describing the relationship between the two variables and the parameter are known as parametric equations.

For a given line, \(l\), any vector \( \vec{d} = (a, b) \) which is parallel to the line is a direction vector of the line.

Furthermore, the slope of a line with direction vector \( \vec{d} =(a, b) \) is \(m= \frac{b}{a} \), provided \( a \neq 0 \). If \(a=0\), then the line is vertical.

Parametric equations provide an alternative description of various curves that could be difficult to express in traditional ways, such as \(y = f(x)\).