Lesson Part 1

In This Module

• Students will explore how the first and second derivatives are connected to calculations involving motion.

To begin, let's look at some definitions of key terms we will use throughout this module.

Definitions

Position \(s(t)\) is the location of an object at a value of time \(t\).

Velocity \(v(t)\) is the rate of change of position over time, so

\[v(t) = s'(t)\]

Acceleration \(a(t)\) is the rate of change of velocity over time, so

\[a(t) = v'(t)\]

Also, we know that velocity is the rate of change of position. So acceleration is the rate of change of velocity, which is the rate of change of position, meaning that

\[a(t) = v'(t)= s''(t)\]

So looking at acceleration, the first derivative of velocity is equal to acceleration, and the second derivative of position is equal to acceleration. Now that we have these three very useful definitions of key terms for motion, let's put them to use in the following example.

Application Example

Example 1—Part A

The height of a soccer ball above the ground at time \(t\) after it is kicked into the air, is given by the formula

\[ h(t) = -4.9t^2 + 3.5t + 1 \]

where \( h \) is the height in metres, \( t \) is the time in seconds, and \(t\geq0\).

Since before the ball is kicked the ball is sitting stationary on the ground, we must put a restriction on the value of \(t\). Here we must say that \(t\) is greater than or equal to zero, meaning that our function is only relevant at the point when the ball is kicked and thereafter.

Determine an equation that will calculate the instantaneous rate of change of the height of the ball with respect to time \( t \).

Solution

In this example, the function \(h(t)\) is used as the position function since the position of the ball is referring to the ball's height above the ground.

We are asked to find the instantaneous rate of change of the height of the ball.

When finding the instantaneous rate of change of the height of the ball, we take the position function, \(h(t)= -4.9t^2 + 3.5t + 1\), and we differentiate. Applying the power rule and the sum rule to this function, we get

\[ h'(t) = -9.8t + 3.5 \]

Since we already defined velocity as being the instantaneous rate of change of position, this formula also represents the vertical velocity of the ball as it moves through the air.

Example 1—Part B

The height of a soccer ball above the ground at time \(t\) after it is kicked into the air, is given by the formula

\[ h(t) = -4.9t^2 + 3.5t + 1 \]

where \( h \) is the height in metres, \( t \) is the time in seconds, and \(t\geq0\).

Determine the vertical velocity of the ball \(0.5\) seconds after it is kicked. At what other time will the ball have the same magnitude of vertical velocity (i.e., speed)?

Solution

Let's begin by answering the first part of this question. The function representing the vertical velocity of the ball at time \(t\) is \( h'(t) = -9.8t + 3.5\) m/s.

Since we're looking for the vertical velocity of the ball half a second after it is kicked, we are going to substitute \(t = 0.5\) into the derivative formula, \(h'(t)\).

Substituting \( t = 0.5 \) gives

\[\begin{align*} h'(0.5) &= -9.8(0.5) + 3.5\\ & =-1.4 \text{ m/s}\end{align*}\]

After substituting this value in, we see that the vertical velocity of the ball is \(-1.4\) metres per second.

The negative sign indicates that the height of the ball is decreasing, so the ball is falling.

Therefore, the ball's vertical velocity \(0.5\) s after it is kicked is \(1.4\) m/s downwards.

Now let's address the second part of this question, which was, at what other time will the ball have the same magnitude of velocity—in other words, speed. There is a bit of a clue in this question.

In this case, we are asked for the same magnitude of vertical velocity, so the ball could be travelling in a different direction. So rather than the ball falling downwards, there may be a time when the ball is rising and has the same speed.

Thinking about the original height function, the degree of this height function is \(2\), meaning that the height function is quadratic. That is, the function for the height of the ball is quadratic in time \(t\), which means that there will be two different time points with the same height value (unless this time coincides with the vertex of the parabola).

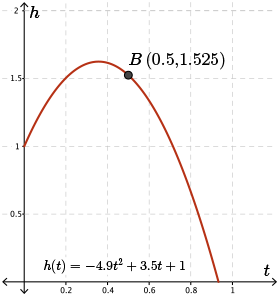
Let's begin by graphing the point on the parabola where \(t=0.5\). In this case, I have labelled this point as point \(B\).

Drawing a horizontal line through this point, we see that the horizontal line also intersects the parabola at another point labelled point \(A\).

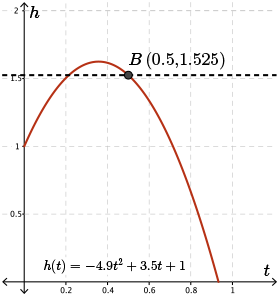
So both point \(A\) and point \(B\) have the same height value at different values of \(t\).

If we visualize these two points on the curve, the tangent lines to the points will be equal in steepness but opposite in direction (i.e., their slopes will be of opposite sign).

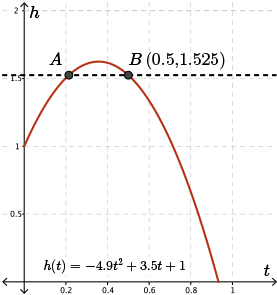
The tangent drawn to point \(A\) has a positive slope whereas the tangent drawn to point \(B\) has a negative slope. A positive slope tells us that the ball is rising, whereas a negative slope tells us the ball is falling.

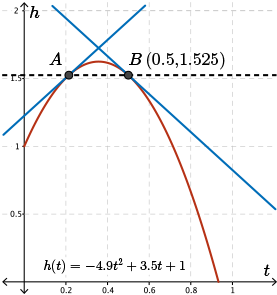
Since these lines are equal in steepness, the speed of the ball at each of these points is the same, although the velocity of the ball is not the same since in these two cases, the direction of travel of the ball is opposite.

Intuitively, at these two points, the ball will have the same magnitude of vertical velocity (i.e., speed) while rising as it does when falling. \( h'(0.5)=-1.4\) m/s. The negative sign implies that the ball is falling when \(t=0.5\) s.

So, to find the point where the ball has the same vertical speed while rising, substitute \( h'(t) = +1.4\) m/s to solve for \( t \).

In other words, let's solve for when the vertical velocity is \(0.4\) m/s upwards rather than downwards. Solving for \(t\) after we substitute \(1.4\) into the function \(h'(t)\), we have

\[\begin{align*} h'(t) &= -9.8t + 3.5 \\ 1.4 &= -9.8t + 3.5 \\ t &\approx 0.21 \text{ s} \end{align*}\]

Therefore, when \(t\) is approximately equal to \( 0.21\) s, the soccer ball would also have a vertical speed of \(1.4\) m/s, but its vertical velocity would be positive (i.e., rising) rather than negative (i.e., falling).

Example 1—Part C

The height of a soccer ball above the ground at time \(t\) after it is kicked into the air, is given by the formula

\[ h(t) = -4.9t^2 + 3.5t + 1 \]

where \( h \) is the height in metres, \( t \) is the time in seconds, and \(t\geq0\).

At what point will the ball reach its maximum height? What is the maximum height reached by the ball?

Solution

Again, let's look at the graph of the height of the ball above the ground.

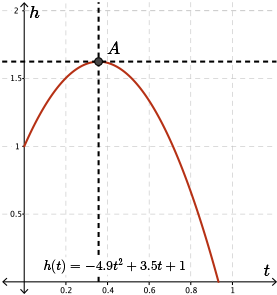
The ball reaches its maximum height when it transitions from rising to falling.

At this point, the vertical height of the ball momentarily does not change. It's like the ball is suspended in mid air. Well if the vertical height of the ball is not changing, we know that the instantaneous rate of change of the height of the ball is equal to zero.

So, the ball reaches its maximum height when the change in the vertical height is \(0\). In other words, \(h'(t) = 0\).

Substituting \(h'(t)=0\) and solving for its corresponding value of \(t\), we get that

\[\begin{align*}h'(t) &= -9.8t + 3.5 \\ 0 &= -9.8t + 3.5 \\ 9.8t & = 3.5 \\ t & = \dfrac{3.5}{9.8} \approx 0.357 \text{ s}\end{align*}\]

Now that we know when the maximum height of the ball will occur, we can take this time value and substitute it into our function for height to determine the maximum height of the ball.

Therefore, the maximum height reached by the ball is approximately,

\[\begin{align*}h(t) & = -4.9t^2 + 3.5t + 1 \\ h(0.357) &= -4.9(0.357)^2 + 3.5(0.357) + 1 \\ h_{\text{ max}} & = 1.625 \text{ m}\end{align*}\]

We can confirm this value by using the graph. Notice that at points where the graph is at a maximum (or minimum) the tangent line is horizontal and the derivative is equal to \(0\). This will be a concept that we use quite often when we explore other applications of the derivative.

Example 1—Part D

The height of a soccer ball above the ground at time \(t\) after it is kicked into the air, is given by the formula

\[ h(t) = -4.9t^2 + 3.5t + 1 \]

where \( h \) is the height in metres, \( t \) is the time in seconds, and \(t\geq0\).

What is the instantaneous vertical velocity of the ball as it hits the ground?

Solution

The ball hits the ground when its height is \(0\). In other words, \( h(t) = 0 \). So we now know a value that we can use to find an answer to this problem. Let's substitute \(h(t)=0\) into our function for height.

\[0 = -4.9t^2 + 3.5t + 1 \]

Solving for \(t\) by using the quadratic formula, we have

\[\begin{align*}t &= \dfrac{-3.5 \pm \sqrt{3.5^2 - 4(-4.9)(1)}}{2(-4.9)} \\ t & = \dfrac{-3.5 \pm \sqrt{31.85}}{-9.8} \\ t & \approx -0.219 \text{ s or } 0.933 \text{ s}\end{align*}\]

We arrive at two values of \(t\): \(t\approx - 0.219\) s or \(t\approx 0.933\) s.

Since we originally defined \( t \geq 0 \), the ball hits the ground when \( t \approx 0.933\) s.

Now that we have this value of \(t\), substitute \( t = 0.933\) s into \( h'(t) \) to find the vertical velocity of the ball when it hits the ground:

\[ h'(0.933) = -9.8(0.933) + 3.5 = -5.64 \text{ m/s}\]

Therefore, the instantaneous vertical velocity of the ball upon impact with the ground is \(-5.64\) m/s.

We can see this velocity on the graph by examining the slope of the tangent to the second zero of the parabola.

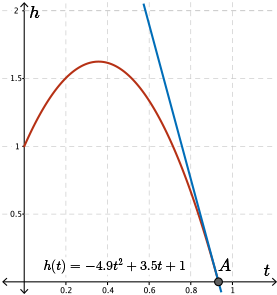
This vertical velocity is shown geometrically by the slope of the tangent line in the diagram.

Quiz

See the first quiz in the side navigation.