Lesson Part 1

Introduction

Recall that the function \( f(x) = e^x \) has the inverse function \( f^{-1}(x) = \ln(x)\).

Let's investigate the slope of the tangent to many points along the curve of \(f(x)=\ln(x)\) by using the following Maple investigation. In this investigation, you will see the graph of \(f(x)=\ln(x)\) and a tangent drawn at one point on the left side of the graph. Maple has calculated the slope of this tangent and then plotted the \(x\)-coordinate of the point of tangency with the value of the slope of the tangent at that point. As you click on the point of tangency and drag this point towards the right side of the grid, you will see many points plotted. These points are the numerical values of the derivative of \(f(x)=\ln(x)\). In other words, we are graphing \(f'(x)\).

Try it now. Examine these points and visualize the function that would be created if we were to connect these values. If we were to connect these values, what function do you see?

Investigation

See the investigation in the side navigation.

Lesson Part 2

Differentiating the Natural Logarithm Function

From the investigation, the first derivative function looked like the following graph. Where have we seen a graph that resembled this? Well, if we consider its properties, we might be able to pinpoint which function this is.

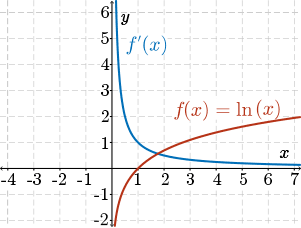
The graph shown has a vertical asymptote of \(x=0\) and a horizontal asymptote of \(y=0\). Does this remind you of a parent function we have looked at in previous math courses?

The function \(y=\dfrac{1}{x}\) has both of these properties, but since the domain of \(f(x)=\ln(x) \) is \(\{x\mid x \gt 0\), \(x\in \mathbb{R} \}\), the derivative function will only be defined for \(x \gt 0\). Also, the numerical values of the tangent slopes at \(x\) seem to be the reciprocals, \(\dfrac{1}{x}\). So when \(x=2\), \(y=\dfrac{1}{2}\); when \(x=3\), \(y=\dfrac{1}{3}\).

So, our educated guess is that the derivative of the function \(f(x)=\ln(x) \) is \(f'(x)=\dfrac{1}{x}\).

Let's use an algebraic method to determine the derivative of \(\ln(x)\). In other words, confirm that the derivative of \(f(x)=\ln(x) \) is \(f'(x)=\dfrac{1}{x}\).

This time, rather than using the definition of the derivative, we are going to use the differentiation rules that we already know. We begin by converting \(y=\ln(x)\) into an exponential function because this is a rule of differentiation that we have previously learned.

The equation:

\[y=\ln(x) \]

converts to:

\[e^y=e^{\ln(x) }=x\]

by exponentiating both sides of the equation.

Now, let's implicitly differentiate this equation with respect to \(x\).

\[\begin{align*} \dfrac{d}{dx} \Big (e^y \Big )&=\dfrac{d}{dx} \Big ( x\Big )&\\ e^y\left ( \dfrac{dy}{dx}\right )&=1&\text{(by the chain rule)}\\ \dfrac{dy}{dx}&=\dfrac{1}{e^y} \end{align*}\]

But from above, we know that \(e^y=x\). Therefore,

\[\dfrac{dy}{dx}=\dfrac{1}{x}\]

The Derivative of the Natural Logarithm: \(f(x)=\ln(x) \)

If \( f(x) = \ln(x)\), then \( f'(x) = \dfrac{1}{x} \) for all \(x \gt 0\).

Lesson Part 3

Examples

So we have a new differentiation rule. Let's put this rule to use in an example.

Example 1

Differentiate \( y = \ln{(x^3)} \).

Solution

There are two methods that we could use to differentiate this expression. Let's start with method \(1\). In method \(1\) we will use the chain rule.

Method 1: Chain Rule

The function \( y = \ln{(x^3)} \) has inner function \(u=x^3\) and outer function \(y=\ln(u)\).

To differentiate this composite function, we apply the chain rule:

\[\begin{align*} \dfrac{dy}{dx}&=\left ( \dfrac{dy}{du}\right ) \left(\dfrac{du}{dx}\right)\\ &= \dfrac{1}{u} \left( 3x^2 \right)\\ &= \dfrac{3x^2}{x^3}\\ &= \dfrac{3}{x} \text{ provided }x \gt 0 \end{align*}\]

Method 2: Applying Laws of Logarithms Before Differentiating

Recall the law of logarithm that states that \( \log_{a} (x^n) = n \log_{a} (x) \).

So the function \( y = \ln(x^3)\) can be expressed as \(y = 3 \ln(x) \).

Now, let's differentiate this expression.

\[\frac{dy}{dx} = 3 \left(\frac{1}{x}\right)=\frac{3}{x} \text{ provided }x \gt 0\]

Note:

We must always remember to consider the domain of \(f(x)\) when differentiating to find \(f'(x)\). Also, differentiation may introduce further constraints (e.g., the domain of \(f(x)=x^{\frac{1}{3}}\) is \(x\in \mathbb{R}\) but the domain of \(f'(x)=\dfrac{1}{3x^{\frac{2}{3}}}\) is all \(x\neq 0\)). Once the domains of \(f(x)\) and \(f'(x)\) are determined, both of these restrictions must be stated for \(f'(x)\). Remember to always include this after you differentiate a function.

Lesson Part 4

Examples

Example 2

Differentiate \( y = \ln{\left(6x^{\frac{5}{3}}\right)} \), by first applying the chain rule. Then differentiate this expression again by applying the laws of logarithms before differentiating.

Solution

Method 1: Chain Rule

The function \( y = \ln{\left(6x^{\frac{5}{3}}\right)} \) has inner function \(u=6x^{\frac{5}{3}}\) and outer function \(y=\ln(u)\).

To differentiate this composite function, we apply the chain rule.

\[\begin{align*} \dfrac{dy}{dx}&=\left ( \dfrac{dy}{du}\right ) \left(\dfrac{du}{dx}\right)&\\ &= \dfrac{1}{u}\left[6\left(\dfrac{5}{3} x^{\frac{2}{3}}\right)\right]&\\ &= \dfrac{10x^{\frac{2}{3}}}{6x^{\frac{5}{3}}}& \text{substitute }u=6x^{\frac{5}{3}}\\ &=\dfrac{5}{3x}&\text{simplify} \end{align*}\]

Now what is the domain of the derivative? The function \(\dfrac{5}{3x}\) is defined for all \(x\neq 0\). But careful, as this is not the domain of \(\dfrac{dy}{dx}\).

Since \(y=\ln\left(6x^{\frac{5}{3}}\right)\), the domain of \(y=f(x)\) is \(x\gt 0\). This is because if \(x\leq0\), then \(x^{\frac{5}{3}}\) is also less than or equal to \(0\). And so \(y=f(x)\) would not be defined there. Therefore, the derivative cannot be defined on any \(x\leq0\), as we cannot talk about the derivative at a point that is not in the domain of \(y=f(x)\).

Since \(\dfrac{5}{3x}\) is defined for all \(x\neq 0\) (and in particular, for all \(x\gt 0\)) the domain of the derivative \(\dfrac{dy}{dx}=\dfrac{5}{3x}\) is also \(x\gt 0\).

Method 2: Logarithm Laws

In method two, we'll use the laws of logarithms before differentiating. Recall the law of logarithm that states that \( \log_{a} (xy) = \log_{a} (x) + \log_{a} (y)\) if \(x,\ y\gt 0\).

So the function \(y = \ln{(6x^{\frac{5}{3}})} \) can be expressed as

\[\begin{align*} y&= \ln(6) + \ln\left(x^{\frac{5}{3}}\right)&\\ &= \ln(6) + \dfrac{5}{3}\ln(x) &\text{since }x\gt 0 \end{align*}\]

When a function has two terms, we differentiate each of these terms separately. So let's look at the first term, which is \(\ln(6)\). Since \(\ln(6)\) is a constant, differentiating this term will lead us to \(0\). So really, we just have to differentiate the expression, \(\dfrac{5}{3}\ln(x)\).

So differentiating \(y=\ln(6) + \dfrac{5}{3}\ln(x) \) gives

\[\begin{align*} \frac{dy}{dx}&= 0 + \dfrac{5}{3} \left(\dfrac{1}{x}\right)\\ &= \dfrac{5}{3x} \end{align*}\]

Again, we note that the domain of the derivative \(\dfrac{dy}{dx}=\dfrac{5}{3x}\) is \(x\gt 0\).

Lesson Part 5

Examples

Example 3

Differentiate \( y = \ln{\left(\dfrac{x+3}{x^3}\right)} \).

Solution

Before differentiating \( y = \ln{\left(\dfrac{x+3}{x^3}\right)} \), did you remember to consider its domain? Let's consider it now.

The expression \(\dfrac{x+3}{x^3}\) is not defined when \(x=0\).

To find the \(\ln\) of this expression, we must have \(\dfrac{x+3}{x^3} \gt 0\). This will only occur when \(x \gt 0\) or \(x \lt -3\).

Thus, the domain of the function \( y = \ln{\left(\dfrac{x+3}{x^3}\right)} \) is \(\{x\mid x \gt 0 \text{ or } x \lt -3, x\in \mathbb{R} \}\). Using graphing technology, we can see this domain.

We could apply the chain rule to differentiate this composite function. This would require us to differentiate the inner function, \( u = \dfrac{x + 3}{x^3} \) using quotient rule, then substituting this derivative for \(\dfrac{du}{dx}\) in \( \dfrac{dy}{dx} = \left (\dfrac{dy}{du}\right )\left(\dfrac{du}{dx}\right) \). This method would be more complicated than using the laws of logarithms to first modify the function before differentiating.

So instead, let's recall the law of logarithm that states that \( \log_{a} \left(\dfrac{x}{y}\right) = \log_{a} (x) - \log_{a} (y)\).

So the function \( y = \ln{\left(\dfrac{x+3}{x^3}\right)} \) can be expressed as

\[\begin{align*} y&= \ln(x + 3) - \ln{(x^3)}\\ &= \ln{(x + 3)} - 3 \ln(x) \end{align*}\]

Differentiating this expression gives,

\[\begin{align*} \dfrac{dy}{dx}&= \dfrac{1}{(x+3)} (1)- 3 \left(\dfrac{1}{x}\right)\\ &= \dfrac{1}{x+3}- \dfrac{3}{x} \end{align*}\]

provided \(x \gt 0\) or \(x \lt -3\).

Note:

Using the law of logarithm hides part of the restriction on the domain of the original function. That is one reason why it is very important to always consider the domain of \(f(x)\) and \(f'(x)\) as we differentiate logarithmic functions, especially when we are using laws of logarithms to modify the original function.

Lesson Part 6

Examples

Are you ready for a more challenging question? Let's try this one.

Challenge Question

Determine the equation of the tangent line drawn to the graph of \(y=x\ln(x)\), which has a slope of \(3\).

Solution

If we are trying to find the equation of a tangent, we need two pieces of information to do so: we need the value of its slope and we need a point of tangency. Here we already know the value of the slope: it is \(3\).To begin, we need to determine the position of the point of tangency to the curve \(y=x\ln(x) \) that has a tangent line with slope \(3\).

So let's start by differentiating the function \(y=x\ln(x)\):

\[\begin{align*} \frac{dy}{dx}&=1(\ln(x) )+x\left(\dfrac{1}{x}\right) &\text{(applying the product rule)}\\ &=\ln(x) +1 &\text{provided }x \gt 0 \end{align*}\]

Since the slope of the tangent is \(3\), we know that \(\dfrac{dy}{dx}=3\).

Substituting \(\dfrac{dy}{dx}=3\) into the derivative equation and solving for \(x\), we have

\[\begin{align*} 3&=\ln(x) +1\\ \ln(x) &=2 \end{align*}\]

Converting the logarithmic equation into an exponential equation, gives

\[x=e^2\]

Now that we know that \(x=e^2\), let's determine its corresponding value of \(y\) by substituting \(x=e^2\) into \(y=x\ln(x) \),

\[y=e^2\left(\ln{(e^2)}\right)=2e^2\left(\ln(e)\right)=2e^2(1)=2e^2\]

Therefore, the point of tangency is at \(\left(e^2,2e^2\right)\).

Now, we use the slope-point equation of a line, \(y-y_1=m(x-x_1)\), along with the slope value \(3\) and point of tangency \(\left(e^2,2e^2\right)\) to determine the equation of the tangent.

\[\begin{align*} y-2e^2&=3\left(x-e^2\right)\\ y&=3x-3e^2+2e^2\\ &=3x-e^2 \end{align*}\]

Therefore, the equation of the tangent line drawn to the graph of \(y=x\ln(x) \) having a slope of \(3\) is \(y=3x-e^2\).

Quiz

See the quiz in the side navigation.