Lesson Part 1
In This Module
We will examine the derivatives of the sine and cosine functions both graphically and using the formal definition of the derivative.
Derivative of \(\sin(x)\)
Recall the graph of the function \(f(x)=\sin(x)\), where \(x\) is in radians. Here we see a picture of the sine curve over the interval from \(-2\pi\) to \(2\pi\).
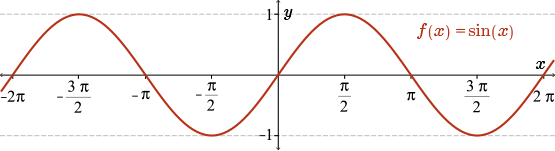
At this point, we are familiar with how to sketch the graph of the first derivative, \(f'(x)\), of a function, given a graph of the original function \(f(x)\).
Starting with a sketch of the function \(f(x)=\sin(x)\), take some time now and try to produce a rough sketch of the graph of the derivative. Pay special attention to the horizontal tangents (when the derivative is \(0\)) and when the slope is positive or negative. Try this now.
Now that we have a rough sketch of the derivative, we can further explore the derivative of \(\sin(x)\) using the following Maple investigation. In this investigation, you will see the graph of \(f(x) = \sin(x)\) and a tangent line drawn at one point on the left side of the graph. If you use the slider to slide the point on the graph to the right, you will see a numerical computation of the slopes of tangent lines to the function \(y=\sin(x)\) at numerous points as the tangent travels from the left side to the right side of the graph. Simultaneously, you will also see a graph appear that is plotting the numerical values \((x, f'(x))\) on the same set of axes. This is giving a rough sketch of the shape of the derivative, \(f'(x)\). If we were to draw a continuous curve through these plotted points, what function would you see? How close is this sketch of the derivative to your own?
Investigation 1
See investigation 1 in the side navigation.
Lesson Part 2
Derivative of \(\sin(x)\)
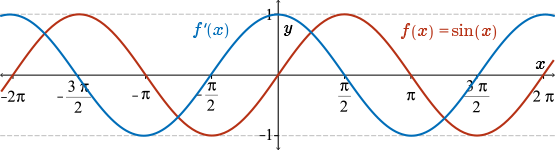
From the Maple investigation, we see that the first derivative of \(f(x) = \sin(x)\) has the following shape. Here we see the graph of \(f(x)=\sin(x)\) and \(f'(x)\) sketched on the same set of axes:
Consider the graph over the interval \([-\pi,\pi]\), as we know the function \(\sin(x)\) is \(2\pi\) periodic:
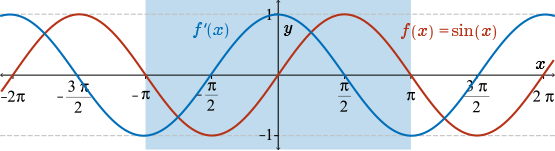
We make the following observations about \(f'(x)\):
- \(f'(x) = 0\) at the points \(x = \pm \dfrac{\pi}{2}\), corresponding to the points at which \(f(x) = \sin(x)\) has horizontal tangents
- \(f'(x) \lt 0\) on \(\left[ -\pi , -\dfrac{\pi}{2} \right]\), \(f'(x) \gt 0\) on \(\left[-\dfrac{\pi}{2} ,\dfrac{\pi}{2} \right]\), and \(f'(x) \lt 0\) on \(\left[ \dfrac{\pi}{2} , \pi \right]\), corresponding to when the slope of the sine curve is positive and negative (this is also reflected in the graph where the derivative is below the \(x\)-axis or above the \(x\)-axis)
- the graph of \(f'(x)\) satisfies \(-1 \leq f'(x) \leq 1\)
- the function \(f'(x)\) achieves its maximum value of \(1\) at the point \(x = 0\), and its minimum value of \(-1\) at the points \(x = \pm \pi\) in our interval
This tells us that the steepest slopes occur at these points, \(x=0\) and \(x=\pm \pi\). In particular, it tells us that when the function \(f(x)=\sin(x)\) passes through the origin, it does so with a slope of \(1\). Similarly, when it passes through \(x=\pm\pi\), it does so with a slope with \(-1\). This analysis, along with the above sketch, provides good evidence that \(f'(x) = \cos(x)\).
Let's confirm the graphical evidence by applying the definition of the derivative to the function \(f(x)=\sin(x)\).
Here we recall the definition of the derivative
\[f'(x)=\lim_{h \rightarrow 0} \dfrac{f(x+h) - f(x)}{h}\]
Now, remember here that \(x\) and \(h\) are both measured in radians. Substituting \(f(x)=\sin(x)\)
\[f'(x)= \lim_{h \rightarrow 0} \dfrac{\sin(x+h) - \sin(x)}{h}\]
Now, we're going to try and compute this limit. First thing, we apply the addition law for the sine function, \(\sin(A+B) = \sin(A)\cos(B) + \cos(A)\sin(B)\):
\[f'(x)=\lim_{h\rightarrow 0} \dfrac{\sin(x)\cos(h) + \cos(x)\sin(h)- \sin(x)}{h}\]
The rest of the terms remain the same. Here with some rearranging, we can factor out the common term of sine x in the first and the third term in the numerator. And so we have
\[\begin{align*} f'(x)&=\lim_{h \rightarrow 0} \dfrac{\sin(x) \cos(h) - \sin(x) + \cos(x) \sin(h)}{h}\\ &=\lim_{h \rightarrow 0} \left[ \dfrac{\sin(x) \left(\cos(h) - 1\right) + \cos(x) \sin(h)}{h} \right] \end{align*}\]
Next, we divide through by \(h\) and get the following two terms
\[f'(x)=\lim_{h \rightarrow 0} \left[ \sin(x) \left(\dfrac{(\cos(h) - 1)}{h}\right) + \cos(x) \left(\dfrac{\sin(h)}{h}\right) \right]\]
We isolate the terms involving \(h\). Here we have a sum of two terms, each term being a product. So using the limit laws for sums and products, we can rewrite this limit as
\[f'(x)=\lim_{h \rightarrow 0} \Bigr[\sin(x)\Bigr] \cdot \displaystyle \lim_{h \rightarrow 0}\left[\dfrac{\cos(h) - 1}{h} \right] + \displaystyle \lim_{h \rightarrow 0} \Bigr[\cos(x)\Bigr] \cdot \displaystyle \lim_{h \rightarrow 0}\left[\dfrac{\sin(h)}{h} \right]\]
provided that each of these four limits indeed exists.
Since \(x\) is a constant when we are computing a limit with respect to \(h\), we have
\[ \lim_{h \rightarrow 0} \Bigr[\sin(x)\Bigr] = \sin(x) \hspace{10mm} \lim_{h \rightarrow 0} \Bigr[\cos(x)\Bigr]= \cos(x)\]
and so the expression becomes
\[f'(x) = \sin(x)\cdot \lim_{h \rightarrow 0}\left[\frac{\cos(h) - 1}{h} \right] + \cos(x)\cdot \lim_{h \rightarrow 0}\left[\frac{\sin(h)}{h} \right] \]
Neither of the above functions of \(h\) are defined at \(h=0\), and our limit laws are not helpful here. We will do some numerical analysis to examine the behaviour of these functions as \(h\) approaches \(0\) from the left and from the right.
Consider the following table of values:
| \(h\) |
\(\dfrac{\sin(h)}{h}\) |
\(\dfrac{\cos(h)-1}{h}\) |
| \(1\) |
\(0.8414709848\) |
\(-0.4596976941\) |
| \(0.5\) |
\(0.9588510772\) |
\(-0.2448348762\) |
| \(0.4\) |
\(0.9735458558\) |
\(-0.1973475150\) |
| \(0.3\) |
\(0.9850673557\) |
\(-0.1488783697\) |
| \(0.2\) |
\(0.9933466540\) |
\(-0.0996671110\) |
| \(0.1\) |
\(0.9983341665\) |
\(-0.0499583470\) |
| \(0.05\) |
\(0.9995833854\) |
\(-0.0249947920\) |
| \(0.01\) |
\(0.9999833334\) |
\(-0.0049999600\) |
| \(0.001\) |
\(0.9999998333\) |
\(-0.0005000000\) |
| \(h\) |
\(\dfrac{\sin(h)}{h}\) |
\(\dfrac{\cos(h)-1}{h}\) |
| \(-1\) |
\(0.8414709848\) |
\(0.4596976941\) |
| \(-0.5\) |
\(0.9588510772\) |
\(0.2448348762\) |
| \(-0.4\) |
\(0.9735458558\) |
\(0.1973475150\) |
| \(-0.3\) |
\(0.9850673557\) |
\(0.1488783697\) |
| \(-0.2\) |
\(0.9933466540\) |
\(0.0996671110\) |
| \(-0.1\) |
\(0.9983341665\) |
\(0.0499583470\) |
| \(-0.05\) |
\(0.9995833854\) |
\(0.0249947920\) |
| \(-0.01\) |
\(0.9999833334\) |
\(0.0049999600\) |
| \(-0.001\) |
\(0.9999998333\) |
\(0.0005000000\) |
Here, we're starting with \(h=-1\) and letting \(h\) slowly approach \(0\) from the left. From the table, it looks like the quotient \(\dfrac{\sin(h)}{h}\) is approaching \(1\). Similarly, if we start at the value of \(h=1\) and let \(h\) slowly approach \(0\) from the right, it appears that the value of \(\dfrac{\sin(h)}{h}\) is approaching \(1\).
Making similar observations for the second column in terms of the cosine function, we see that these numerical values are approaching something close to \(0\) from the left and from the right. As suggested by the numerical data, we guess that the limits are \(1\) and \(0\) respectively.
In fact, this is indeed the case:
\[\displaystyle \lim_{h \rightarrow 0}\left[\frac{\sin(h)}{h} \right]=1 \ \hspace{1 cm}\text{and} \hspace{1 cm} \ \lim_{h \rightarrow 0}\left[\frac{\cos(h) - 1}{h} \right]=0\]
The formal proofs of these limits are not presented here, but they can be shown using a geometric argument and a result called the squeeze theorem.
Substituting these limits into our original expression for \(f'(x)\), we get
\[\begin{align*} f'(x)=& \sin(x) \cdot \lim_{h \rightarrow 0}\left[\frac{\cos(h) - 1}{h} \right] + \cos(x) \cdot \lim_{h \rightarrow 0}\left[\frac{\sin(h)}{h} \right] \\ &= \sin(x) (0) + \cos(x) (1) \\ &= \cos(x) \end{align*}\]
We get the following differentiation formula:
\[\dfrac{d}{dx}\Big(\sin(x)\Big) = \cos(x)\]
Now it's important to note here that the limit calculations we attempted to verify our only valid if we're taking \(h\) in radians. You can examine for yourself what happens to \(\dfrac{\sin(h)}{h}\) or \(\dfrac{\cos(h-1)}{h}\) if we measure \(h\) in degrees. You will do some analysis of this in the student exercises at the end of this module. For now, we note that this differentiation formula only holds if we're measuring \(x\) in radians.
Lesson Part 3
Derivative of \(\cos(x)\)
This time we start with the graph of the function \(f(x)=\cos(x)\), where \(x\) is in radians. Here we see a sketch over the interval from \(-2\pi\) to \(2 \pi\).
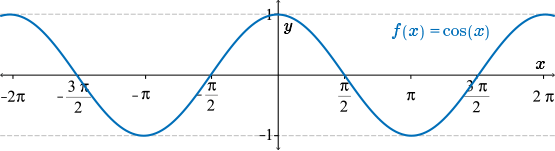
Starting with a sketch of the function \(f(x)=\cos(x)\), take some time now and try to produce a rough sketch of the first derivative \(f'(x)\). Again, we pay special attention to things like horizontal tangents and when the slope is positive or negative.
We can further explore the derivative of \(\cos(x)\) using a similar Maple investigation to that used in the case of the sine function. As Maple plots the derivative of the cosine function at numerous points, what function do you see? How close is this sketch of the derivative to your own?
Investigation 2
See investigation 2 in the side navigation.
Lesson Part 4
Derivative of \(\cos(x)\)
Again, the derivative sketched here looks similar to our trigonometric functions. In fact, it looks like the function \(-\sin(x)\).
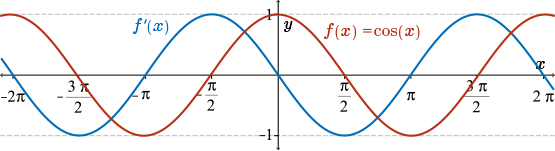
Based on the above sketch, we suspect that \(f'(x) = -\sin(x)\).
Let's confirm our guess using the identity
\[\sin^{2}(x) + \cos^{2}(x) = 1\]
and the fact that
\[\dfrac{d}{dx}\Big(\sin(x)\Big) = \cos(x)\]
Differentiating the above identity implicitly, with respect to \(x\), and using the chain rule, we get
\[\begin{align*} \dfrac{d}{dx}\left(\sin^{2}(x) + \cos^{2}(x) \right) &= \dfrac{d}{dx}\left((\sin(x))^{2} + (\cos(x))^{2} \right) \\ &= 2 \sin(x) \left( \dfrac{d}{dx}\Big(\sin(x)\Big)\right) + 2 \cos(x) \left( \dfrac{d}{dx}\Big(\cos(x)\Big)\right)\\ &= 0 \end{align*}\]
Of course, the derivative of the right hand side is the derivative of \(1\), which is a constant, so it's \(0\). Substituting the fact that \(\dfrac{d}{dx}\Big(\sin(x)\Big) = \cos(x)\), we get
\[2 \sin(x)\cos(x)+ 2 \cos(x) \left( \dfrac{d}{dx}\Big(\cos(x)\Big)\right) = 0\]
Next, we isolate the term \(\dfrac{d}{dx}\Big(\cos(x)\Big)\) as follows:
\[\begin{align*} 2 \cos(x) \left( \dfrac{d}{dx}\Big(\cos(x)\Big)\right)&= -2 \sin(x)\cos(x)\\ \dfrac{d}{dx}\Big(\cos(x)\Big)&=-\dfrac{2 \sin(x)\cos(x)}{2 \cos(x)} \hspace{1 cm}\text{provided }\cos(x)\neq 0\\ &= -\sin(x) \end{align*}\]
we conclude that \(\dfrac{d}{dx}\Big(\cos(x)\Big) = -\sin(x)\) as desired.
Note: Using limits, we can show that this formula also holds for values of \(x\) for which \(\cos(x)=0\).
We get the following differentiation formula:
\(\dfrac{d}{dx}\Big(\cos(x)\Big) = -\sin(x)\)
This formula only holds if \(x\) is measured in radians.
Lesson Part 5
Examples
Now let's apply these to new differentiation formulas in some examples.
Example 1—Part A
Find the derivative of the following function.
\[f(x) = \sin(3x+2)\]
Solution—Part A
Now, here we have a composition of functions where the outer function is the sine function. And we know that \(\dfrac{d}{du}\Big(\sin(u)\Big)= \cos(u)\) for any variable \(u\). So using the chain rule, we have
\[\begin{align*} f'(x) &= \cos(3x+2) (3) \\ &= 3 \cos(3x+2) \end{align*}\]
Example 1—Part B
Find the derivative of the following function.
\[f(x) = e^{x}\cos(x)\]
Solution—Part B
Here we have a product of functions, so we need to use the product rule, along with the differentiation formula for cosine. By the product rule, we have
\[\begin{align*} f'(x)&= e^{x} \left( \dfrac{d}{dx}\Big(\cos(x)\Big)\right) + \cos(x)\left(\dfrac{d}{dx}\Big(e^{x}\Big)\right)\\ &= e^{x}(-\sin(x)) + \cos(x)\left(e^{x}\right)\\ &=e^{x}(\cos(x)-\sin(x)) \end{align*}\]
Example 1—Part C
Find the derivative of the following function.
\[f(x) = \sin(x)\cos\left(x^{2}\right)\]
Solution—Part C
Here we have a product of functions, and one of the functions is a composition of functions. So we should need the product rule and the chain rule here.
\[\begin{align*} f'(x)&=\sin(x) \dfrac{d}{dx}\Big(\cos\left(x^{2}\right)\Big) + \cos\left(x^{2}\right) \dfrac{d}{dx}\Big(\sin(x)\Big)\\ &=\sin(x) \bigr(-\sin\left(x^{2}\right)(2x)\bigr) + \cos\left(x^{2}\right)\cos(x) &\text{since }\ \dfrac{d}{du}\Big(\cos(u)\Big) =-\sin(u)\\ &= -2x\sin(x)\sin\left(x^{2}\right) + \cos(x)\cos\left(x^{2}\right) \end{align*}\]
Lesson Part 6
Examples
Example 2
Find the \(17^{th}\) derivative of \(f(x) = \sin(x)\).
Solution
Now we could go ahead and just try and differentiate the function \(17\) times and see what we spit out. But instead, we're going to look at the first few derivatives of \(f(x) = \sin(x)\) and try and figure out a pattern.
\[\begin{align*} f'(x)&=\cos(x)\\ f''(x)&=-\sin(x)\\ f^{(3)}&=-\cos(x)\\ f^{(4)}&=-(-\sin(x)) = \sin(x)\\ f^{(5)}&=\cos(x) \end{align*}\]
We observe that the successive derivatives follow a pattern. In particular, the cycle of the four functions \(\{\sin(x), \cos(x), -\sin(x), -\cos(x)\}\) repeats indefinitely. So we don't actually have to compute the \(17^{th}\) derivative. We can just exploit this pattern.
Since \(f^{(4)}(x) = \sin(x)\), this pattern must repeat for all multiples of \(4\). Therefore, we must have \(f^{(4)}(x)=f^{(8)}(x)=f^{(12)}(x)=f^{(16)}(x) = \sin(x)\) as well.
We're looking for the \(17^{th}\) derivative, so differentiating one more time, we get
\[\begin{align*} f^{(17)}(x) &= \dfrac{d}{dx}\left(f^{(16)}(x)\right)\\ &= \dfrac{d}{dx}\Big(\sin(x)\Big)\\ &= \cos(x) \end{align*}\]
Lesson Part 7
Examples
Example 3
Find an equation of the tangent line to the curve \(y = \dfrac{x \sin(x)}{\cos(x) + 1}\) at the point \(\left(\dfrac{\pi}{2},\dfrac{\pi}{2}\right)\).
Solution
So to find an equation of a tangent line, we need the slope of the tangent line and we need a point on the curve. We're given the point on the curve, so we need to find the slope of the tangent line. To do so, we need to first find an expression for the derivative \(f'(x)\).
Here we have a quotient, and so we're going to use the quotient rule. But within the numerator, we have a product. So before we apply the quotient rule, let's first compute the derivative of the numerator using the product rule and the fact that \(\dfrac{d}{dx}\Big(\sin(x)\Big) = \cos(x)\):
\[\begin{align*} \dfrac{d}{dx}\Big(x\sin(x)\Big) &= x \left(\dfrac{d}{dx}\Big(\sin(x)\Big)\right) + \sin(x) \left(\dfrac{d}{dx}\Big(x\Big)\right)\\ &= x \cos(x) + \sin(x) \end{align*}\]
Using the quotient rule, we get
\[\begin{align*} f'(x)&=\dfrac{(\cos(x)+1)\left[{\color{Violet}\dfrac{d}{dx}\Big(x\sin(x)\Big)}\right] - (x\sin(x)) \left[\dfrac{d}{dx}\Big(\cos(x)+1\Big)\right]}{(\cos(x)+1)^{2}}\\ &=\dfrac{(\cos(x)+1)\left[ {\color{Violet} x \cos(x) + \sin(x)}\right] - x \sin(x) \left[-\sin(x)\right]}{(\cos(x)+1)^{2}}\\ &=\dfrac{(\cos(x)+1)\left[ x \left( \cos(x)\right) + \sin(x)\right] + x \sin^{2}(x)}{(\cos(x)+1)^{2}} \end{align*}\]
Now here, we could expand the numerator and attempt to simplify, but instead, we will substitute the value of \(x=\dfrac{\pi}{2}\) into this expression directly:
\[\begin{align*} f'\left(\dfrac{\pi}{2}\right)&=\dfrac{\left({\color{BrickRed}\cos\left(\frac{\pi}{2}\right)}+1\right)\left[ \left(\frac{\pi}{2}\right)\left( {\color{BrickRed}\cos\left(\frac{\pi}{2}\right)}\right) + {\color{NavyBlue}\sin\left(\frac{\pi}{2}\right)}\right] + \left(\frac{\pi}{2}\right) {\color{NavyBlue}\sin^{2}\left(\frac{\pi}{2}\right)}}{\left({\color{BrickRed}\cos\left(\frac{\pi}{2}\right)}+1\right)^{2}}\\ &=\dfrac{\left({\color{BrickRed}0}+1\right)\left[ \left(\frac{\pi}{2}\right) ({\color{BrickRed}0}) + {\color{NavyBlue}1} \right] + \left(\frac{\pi}{2}\right) ({\color{NavyBlue}1})^{2}}{\left({\color{BrickRed}0}+{\color{NavyBlue}1}\right)^{2}}\\ &=\dfrac{(1)(1) + \frac{\pi}{2}}{1}\\ &=\dfrac{\pi}{2}+1\\ &=\dfrac{\pi+2}{2} \end{align*}\]
Therefore, an equation for the tangent line to the curve \(y = \dfrac{x \sin(x)}{\cos(x) + 1}\) at the point \(\left(\dfrac{\pi}{2},\dfrac{\pi}{2}\right)\) is
\[y = \dfrac{\pi}{2} +\left( \dfrac{\pi+2}{2}\right)\left(x-\dfrac{\pi}{2}\right)\]
Note:
It is important to reiterate here that the formulas \(\dfrac{d}{dx}\Big(\sin(x)\Big) = \cos(x)\) and \(\dfrac{d}{dx}\Big(\cos(x)\Big) = -\sin(x)\) only hold if \(x\) is measured in radians. You will explore the case where \(x\) is measured in degrees in the student exercises. This will include an investigation of the trigonometric limits
\[ \displaystyle \lim_{h \rightarrow 0} \dfrac{\sin(h)}{h} \hspace{1 cm}\text{and}\hspace{1 cm} \lim_{h \rightarrow 0} \dfrac{\cos(h)-1}{h}\]
when \(h\) is measured in degrees instead of radians. We note that, in general, when solving calculus problems involving trigonometric functions, \(x\) is measured in radians.
Quiz
See the quiz in the side navigation.