Lesson Part 1

In This Module

• We will examine the derivatives of the tangent function and the reciprocal trigonometric functions graphically.
• We will use the known derivatives of the sine and cosine functions to verify formulas for each of the derivatives.

The Tangent Function

Consider the graph of the tangent function, \(f(x)=\tan(x)\) where \(x\) is measured in radians. Here we see a picture of the graph over the interval from \(-2 \pi\) to \(2 \pi\).

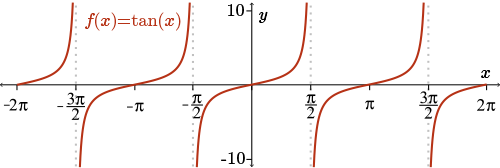
What does the graph of \(f'(x)\) look like? What information can we gather from the graph of \(f(x)=\tan(x)\)?

• Since \(f(x) = \tan(x)\) is undefined at the points \(x = \pm \dfrac{\pi}{2}, \pm \dfrac{3\pi}{2}, \ldots,\) the derivative \(f'(x)\) will be undefined at each of these points as well.
• The slope of \(f(x)\) is always positive and so we have \(f'(x) \gt 0\) for the entire domain of \(f(x)\).
• The slope appears flattest (closest to horizontal) at the points \(x=0, \pm \pi, \pm 2\pi \ldots\) and so we might expect \(f'(x)\) to attain some minimal value at these points. (What the minimal value is is not so clear.)
• The slope is approaching \( + \infty\) as \(x\) approaches any of the vertical asymptotes at \(x = \pm \dfrac{\pi}{2}, \pm \dfrac{3\pi}{2}, \ldots\)

We can use these observations to draw a rough sketch of the derivative \(f'(x)\). Try this now. Does this sketched curve remind you of any known function?

Hopefully, the graph that you sketched looked something like the following:

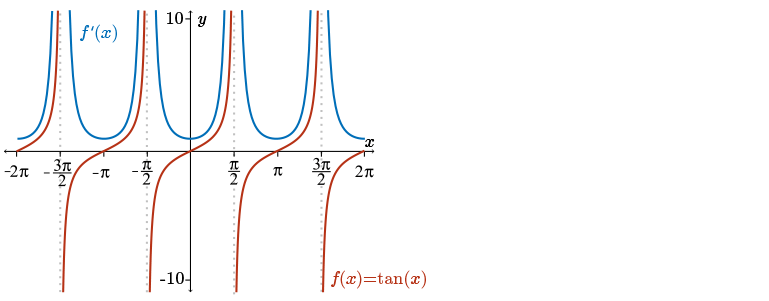
As we'd expect, the derivative, \(f'(x)\) has the same vertical asymptotes as \(f(x)\). And as we predicted, the derivative approaches positive infinity as \(x\) approaches any of the asymptotes from either the left or the right. Also, we see that \(f'(x)\) lies entirely above the \(x\)-axis, and so it's always positive. And the minimum values are occurring where we expected them to - at \(x=0, \pm \pi, \pm 2\pi \ldots\) Perhaps you can estimate what these minimal values are by looking of the graph.

Does the shape of this curve appear similar to the shape of another trigonometric function? Consider the graph of the function \(g(x) = \sec(x)\).

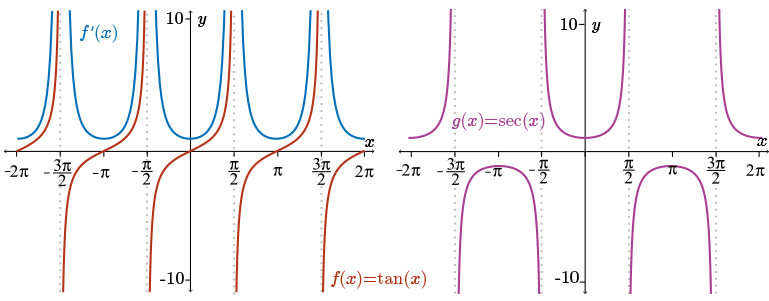
The graph of \(g(x)\) and \(f'(x)\) share the same vertical asymptotes, but there are two observable differences in the graphs. The most obvious one is that the function \(g(x)\) takes on negative values, while \(f'(x)\) is always positive. What does this suggest? Perhaps we're looking at the absolute value of \(g(x)\)? The less obvious difference is that the the function \(f'(x)\) increases faster than the function \(g(x)\). In other words, the slope looks much steeper in the picture of \(f'(x)\) than it does in the picture of \(g(x)\). This suggests that \(f'(x)\) is not the absolute value of \(g(x)\), but perhaps it is the square of \(g(x)\). From the graphical evidence, we suspect that \(f'(x) = (g(x))^{2} = \sec^{2}(x)\).

Since \(\tan(x) = \dfrac{\sin(x)}{\cos(x)}\) and the derivatives of \(\sin(x)\) and \(\cos(x)\) are known, we can confirm this suspicion using the quotient rule.

\[\begin{align*} \dfrac{d}{dx}\Big(\tan(x)\Big)&=\dfrac{d}{dx}\left(\dfrac{\sin(x)}{\cos(x)}\right)\\ &=\dfrac{\cos(x)\dfrac{d}{dx}\Big(\sin(x) \Big)- \sin(x)\dfrac{d}{dx}\Big(\cos(x)\Big)}{\cos^{2}(x)}\\ &=\dfrac{\cos(x)\cos(x) - \sin(x)(-\sin(x))}{\cos^{2}(x)}\\ &=\dfrac{1}{\cos^{2}(x)}\ \hspace{2 cm}\text{since }\ \cos^{2}(x) + \sin^{2}(x) = 1\\ &=\sec^{2}(x) \end{align*}\]

Examples

Example 1

Find the derivatives of the functions \(f(x) = \tan(3x^{2}+4)\) and \(g(x) = \tan(x)\sin(x)\).

Solution

Let's deal with the first function, \(f(x)\). This is a composition of functions where the outer function is \(\tan(x)\) and the inner function is the polynomial \(3x^2+4\). Since \(\dfrac{d}{du}\Big(\tan(u)\Big) = \sec^{2}(u)\) then, using the chain rule, we get

\[\begin{align*} \dfrac{d}{dx}\Big(\tan(3x^{2}+4)\Big)=&\sec^{2}(3x^{2}+4) \dfrac{d}{dx}\Big(3x^{2}+4\Big)\\ &= 6x \sec^{2}(3x^{2}+4) \end{align*}\]

Now onto the second function, \(g(x)\) is a product of two trig functions. By the product rule, we have

\[\begin{align*} \dfrac{d}{dx}\Big(\tan(x)\sin(x)\Big )&=\tan(x) \dfrac{d}{dx}\Big (\sin(x)\Big ) + \sin(x) \dfrac{d}{dx}\Big(\tan(x)\Big)\\ &=\tan(x)\cos(x) + \sin(x)\sec^{2}(x)\\ &=\dfrac{\sin(x)}{\cos(x)} \cos(x) + \sin(x)\sec^{2}(x)\\ &=\sin(x) + \sin(x)\sec^{2}(x)\\ &=\sin(x)(\sec^{2}(x)+1) \end{align*}\]

Lesson Part 2

The Reciprocal Trigonometric Functions

Consider the graph of the function \(f(x) = \cot(x) = \dfrac{1}{\tan(x)}\). If you've forgotten what the graph of the cotangent looks like, we've provided a graph of the tangent function in the background to help. Notice that the cotangent has vertical asymptotes at \(x=0,\pm\pi,\pm2\pi\ldots\), exactly where the tangent function has its zeros.

So what information can we get about the derivative of the cotangent, given this graph?

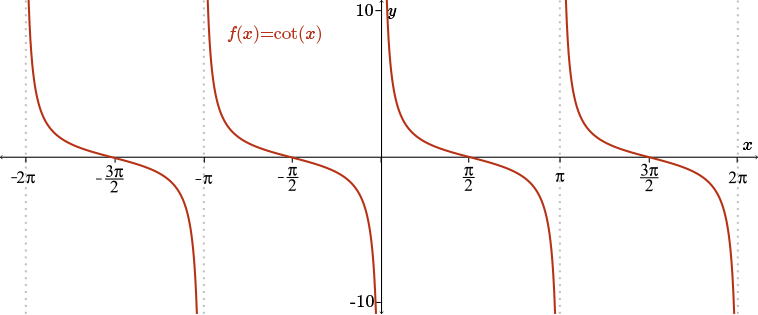
• \(f'(x)\) will be undefined at the points \(x = 0, \pm \pi, \pm 2\pi, \ldots\) just like the cotangent function itself.
• The slope of \(f(x)\) is always negative and so we have \(f'(x) < 0\) for the entire domain of \(f(x)\).
• The slope appears flattest (closest to horizontal) at the points \(x = \pm \dfrac{\pi}{2}, \pm \dfrac{3\pi}{2}, \ldots,\) so \(f'(x)\) attains its maximum value at these points. (Now it might seem strange to talk about a maximum value here, but this is indeed what's happening. Remember that \(f'(x)\) is always negative, and we're looking for where the slope appears flattest, or closest to \(0\); so the negative value of slope that's closest to \(0\) will indeed be a maximum.)
• The slope is approaching \( - \infty\) as \(x\) approaches any of the vertical asymptotes at \(x = 0, \pm \pi, \pm 2\pi, \ldots\) from either the left or the right.

Use this information to sketch the graph of \(f'(x)\). Does this graph remind you of a known trigonometric function?

How close is your sketch to the actual graph of the derivative \(f'(x)\) shown here?

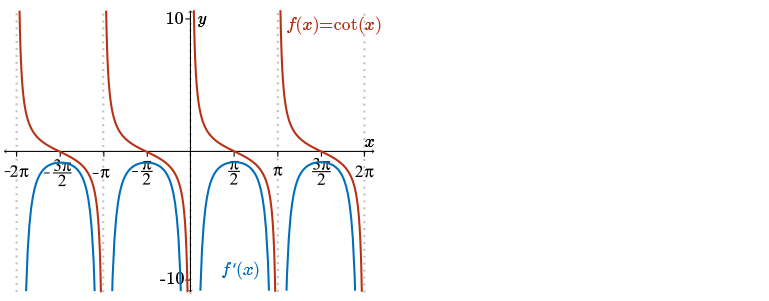
As we predicted, as \(x\) approaches any of the vertical asymptotes, \(f'(x)\) approaches negative infinity. Also observe that the derivative, \(f'(x)\), is always below the \(x\)-axis. This is expected because we observe that the derivative of \(\cot(x)\) is always negative. Finally, we see the maximum values occurring where we expected. See if you can estimate what these max values are from the graph. Does the shape of this curve seem reminiscent of another trigonometric function?

Consider the following graph of the function \(g(x) = \csc(x)\).

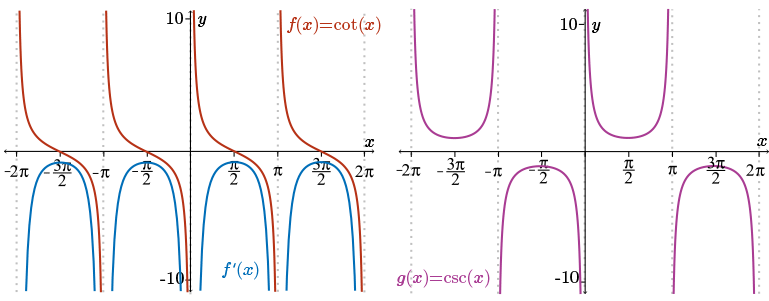
Here we see that the graph \(f'(x)\) and \(g(x)\) share the same vertical asymptotes, but \(f'(x)\) is always negative while \(g(x)\) takes on positive and negative values. Moreover, it appears that the function \(f'(x)\) is decreasing faster than \(g(x)\). In other words, we have a steeper slope in the function \(f'(x)\) than we do in the function \(g(x)\).

These observations suggest a guess that

\[f'(x) = - \csc^{2}(x)\]

Let's confirm this suspicion using the fact that \(\cot(x) = \dfrac{1}{\tan(x)}=(\tan(x))^{-1}\). To differentiate this expression, we need to use the power rule and the chain rule.

\[\begin{align*} \dfrac{d}{dx}\Big(\cot(x)\Big)&=\dfrac{d}{dx}\Big( (\tan(x))^{-1}\Big)\\ &= - (\tan(x))^{-2} \sec^{2}(x)\ &\text{by the power rule and the chain rule}\\ &=- \left (\dfrac{1}{\tan^{2}(x)} \right )\left ( \sec^{2}(x) \right )\\ &=- \left (\dfrac{\cos^{2}(x)}{\sin^{2}(x)} \right ) \left ( \dfrac{1}{\cos^{2}(x)}\right )\\ &=-\dfrac{1}{\sin^{2}(x)}\\ &=- \csc^{2}(x) \end{align*}\]

Examples

Example 2

Find the derivative of \(f(x) = \cot^{3}(2x)\).

Solution

Here we have a composition of functions, and so we will need to use the chain rule. Since \(f(x) = (\cot(2x))^{3}\), we will need to use the power rule and the chain rule. Now notice here that our inner function is also a composition of functions, so we need to apply the chain rule again

\[\begin{align*} f'(x)&=3 (\cot(2x))^{2} \dfrac{d}{dx} \Big(\cot(2x)\Big)\\ &= 3\cot^{2}(2x) (-\csc^{2}(2x))\dfrac{d}{dx}\Big(2x\Big)\ &\text{as } \dfrac{d}{du}\Big (\cot(u)\Big ) = -\csc^{2}(u)\\ &=-3 \cot^{2}(2x)\csc^{2}(2x)(2)\\ &=-6 \cot^{2}(2x)\csc^{2}(2x) \end{align*}\]

The derivatives of the remaining reciprocal trigonometric functions, secant and cosecant, can be found in a similar manner. You will verify the following formulas in the student exercises.

\(\dfrac{d}{dx}\Big (\sec(x) \Big) =\sec(x) \tan(x) \qquad \dfrac{d}{dx}\Big(\csc(x)\Big) = - \csc(x)\cot(x)\)

Lesson Part 3

Examples

Example 3

Let \(f(x) = \dfrac{\tan(x)-1}{\sec(x)}\). Find all values of \(x\) for which the graph of \(f\) has a horizontal tangent.

Solution

To find all the values of \(x\) that have horizontal tangents, we need to find all \(x\) such that \(f'(x)=0\). First, we need an expression for the derivative, \(f'(x)\). Since we have a quotient, we're going to use the quotient rule.

\[\begin{align*} f'(x)&=\dfrac{\sec(x) \dfrac{d}{dx}\Big (\tan(x)-1\Big ) - (\tan(x)-1)\dfrac{d}{dx}\Big (\sec(x)\Big)}{\sec^{2}(x)}\\ &=\dfrac{\sec(x)\sec^{2}(x) - (\tan(x)-1)\sec(x)\tan(x)}{\sec^{2}(x)}\\ &=\dfrac{\sec^{2}(x)-(\tan(x)-1)\tan(x)}{\sec(x)}\\ &= \dfrac{\sec^{2}(x)-\tan^{2}(x)+\tan(x)}{\sec(x)} &\sec^2(x) - \tan^2(x) = 1\\ &=\dfrac{1+\tan(x)}{\sec(x)} &\tan^{2}(x)+1=\sec^{2}(x) \end{align*}\]

Alternatively, we could first rewrite the expression for \(f(x)\) in terms of sine and cosine before differentiating. This will make the differentiation step much simpler (but make sure to keep the domain of the original function in mind). More specifically, if we do so, we would get

\[\begin{align*} f(x)&=\dfrac{\tan(x)-1}{\sec(x)}\\ &=\cos(x)\left(\dfrac{\sin(x)}{\cos(x)}-1\right)\\ &=\sin(x)-\cos(x) \end{align*}\]

provided that \(\cos(x)\neq 0\). (Note that the domain of \(f(x)\) is all \(x\) such that \(\cos(x)\neq 0\).)

Therefore, \(f'(x)=\cos(x)+\sin(x)\) for all \(x\) such that \(\cos(x)\neq 0\). Notice that we have

\[f'(x)=\dfrac{1+\tan(x)}{\sec(x)}=\cos(x)\left(1+\dfrac{\sin(x)}{\cos(x)}\right)=\cos(x)+\sin(x)\]

provided that \(\cos(x)\neq 0\) and so the two formulas for the derivative are equivalent for all \(x\) in the domain of \(f(x)\).

Therefore, we can find the roots of the function \(f'(x)=\dfrac{1+\tan(x)}{\sec(x)}=\cos(x)+\sin(x)\) using either expression. But don't forget that we have the implicit restriction \(\cos(x)\neq0\) if you decide to use the second expression for the derivative. Now, this doesn't end up being crucial in this particular example. But in general, it is a good idea to keep in mind any restriction that we have on the domain.

The function \(f\) has a horizontal tangent if \(f'(x) = 0\). Note that \(\sec(x)=\dfrac{1}{\cos(x)}\neq 0\), so this derivative is defined on the entire domain of the tangent function. Also note that \(\sec(x)\) and \(1+\tan(x)\) have the same domain. So we have \(f'(x) = 0\) exactly when the numerator, \(1 + \tan(x) = 0\) or, equivalently, when \(\tan(x) = -1\).

So which \(x\)-value does this correspond to? From the special triangle \(1,1,\sqrt{2}\) or \(\dfrac{\pi}{4}, \dfrac{\pi}{4}, \dfrac{\pi}{2}\),

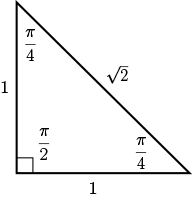
we see that

\[\begin{align*} \tan\left(\dfrac{\pi}{4}\right) &= \dfrac{1}{1}\\ &= 1 \end{align*}\]

So, the reference angle is \(\dfrac{\pi}{4}\).

We're looking for values of \(x\) where \(\tan(x)=-1\). So we want \(\tan(x)\) to be negative (i.e. \(\tan(x) \lt 0\). Thus we are looking for angles in the \(2^{nd}\) and \(4^{th}\) quadrant.

Therefore, we have \(x\)-values: \(x =\dfrac{3\pi}{4}\) in the second quadrant and \(x =\dfrac{7\pi}{4}\) in the fourth quadrant.

Because we have a period of \(\pi\), we pick up \(x =\dfrac{11\pi}{4}\), \(x =\dfrac{15\pi}{4}\), and so on. We can write this list of x-values in a nice, general way

\[\begin{align*} x &=\dfrac{3\pi}{4}, \dfrac{7\pi}{4}, \dfrac{11 \pi}{4}, \dfrac{15\pi}{4}, \ldots \\ &= \dfrac{3\pi}{4} + k\pi, &k \text{ is any integer} \end{align*}\]

And so we conclude that the values of \(x\) for which the graph of \(f\) has a horizontal tangent are all \(x\) of the form \(\dfrac{3\pi}{4} + k\pi\), where \(k\) is any integer.

To finish off this module, you should have a look of the attached Maple investigation. Similar to what we saw with the sine and cosine functions, this investigation will provide you with a rough sketch of the derivatives of all the trig functions studied in this module. You can use this investigation to confirm the sketches that we did by hand for the derivatives of the tangent and the cotangent functions and to explore the derivatives that we didn't specifically look at in this module- the derivatives of the secant function and the cosecant function.

Investigation

See the investigation in the side navigation.

Quiz

See the quiz in the side navigation.