Partial Solutions


  1. There is no solution provided for this question.
    1. Vectors 20 N [N] and 25 N [E] form a resultant vector v with unknown angle theta between v and the 25 N [E] vector\[\begin{align*} \left \lvert \vec{v} \right \rvert^2 &= 20^2 + 25^2 \\ \left \lvert \vec{v} \right \rvert &= 32.0 \\ \tan{(\theta)} &= \frac{20}{25} \\ \theta &= 38.7^\circ \end{align*}\]
       
    2. Vectors 10 N and 12 N placed tail to tail, separated by 45 degrees, form a resultant vector v with unknown angle theta between v and the 12 N [E] vector\[\begin{align*} \left \lvert \vec{v} \right \rvert^2 &= 12^2 + 10^2 - 2 \cdot 12 \cdot 10 \cdot \cos{(135^\circ)} \\ \left \lvert \vec{v} \right \rvert &= 20.3 \\ \frac{\sin{(\theta)}}{10} &= \frac{\sin{(135^\circ)}}{20.3} \\ \theta &= 20.3^\circ \end{align*}\]
       
    3. Vectors 35 N [E] and 40 N [S] form a resultant vector v with unknown theta between v and the 40 N [S] vector\[\begin{align*} \vec{v} &= 40 ~ [N] + 80 ~ [S] + 35 ~ [E] \\ &= 40 ~ [N] + (-80) ~ [N] + 35 ~ [E] \\ &= 40 ~ [S] + 35 ~ [E] \\ \left \lvert \vec{v} \right \rvert^2 &= 40^2 + 35^2 \\ \left \lvert \vec{v} \right \rvert &= 53.2 \\ \tan{(\theta)} &= \frac{35}{40} \\ \theta &= 41.2^\circ \end{align*}\]
       
  3. There is no solution provided for this question.
    1. Vectors a, b, c form a triangle with unknown theta between a and b. a is extended to form an angle 180 - theta with b.\[\begin{align*} \cos{(\theta)} &= \frac{12^2 + 5^2 - 13^2}{2 \cdot 12 \cdot 5} \\ \theta &= 90^\circ \\ 180^\circ - \theta &= 90^\circ \end{align*}\]
       
    2. Vectors a, b, c form a triangle with unknown theta between a and b. a is extended to form an angle 180 - theta with b. \[\begin{align*} \cos{(\theta)} &= \frac{10^2 + 20^2 - 22^2}{2 \cdot 10 \cdot 20} \\ \theta &= 87.7^\circ \\ 180^\circ - \theta &= 92.3^\circ \end{align*}\]
       
    3. Vectors a, b, c form a triangle with unknown theta between a and b. a is extended to form an angle 180 - theta with b. \[\begin{align*} \cos{(\theta)} &= \frac{40^2 + 32^2 - 65^2}{2 \cdot 40 \cdot 32} \\ \theta &= 128.7^\circ \\ 180^\circ - \theta &= 51.3^\circ \end{align*}\]
       
  5. There is no solution provided for this question.
  6. Unknown vector f and v = 100 N [NW] vector are tail to tail with angle alpha between. Vector u = N [S] vector extends from tip of v to tip of f at 45 degrees to v and unknown theta to f. f is extended to form 180 - theta angle with u.
    1. \[\begin{align*} \left \lvert \vec{f} \right \rvert^2 &= 100^2 + 45^2 - 2 \cdot 100 \cdot 45 \cdot \cos{(45^\circ)} \\ \left \lvert \vec{f} \right \rvert &= 75.2 \end{align*}\]
    2. \[\begin{align*} \frac{\sin{(\alpha)}}{45} &= \frac{\sin{(45^\circ)}}{75.2} \\ \alpha &= 25^\circ \\ \theta &= 180^\circ - 45^\circ - 25^\circ \\ 180^\circ - \theta &= 70^\circ \end{align*}\]
  7. There is no solution provided for this question.

  8. The force diagram is shown below.

    Two 150 N vectors form an isosceles triangle with the ceiling with base angles theta. A 196 N vector extends downward from the bottom vertex of the triangle.

    An isosceles vector triangle with equal sides of magnitude 150, and third side of magnitude 196. The angle between the two equal sides is 2(theta) Since the vectors are in equilibrium, we obtain the following vector triangle shown to the right. Solving for \( \theta \),

    \[\begin{align*} \cos{(2\theta)} &= \frac{150^2 + 150^2 - 196^2}{2 \cdot 150 \cdot 150} \\ 2\theta &= 81.6^\circ \\ \theta &= 40.8^\circ \end{align*}\]
     
    To solve for the distance between the two anchor points of the wires, consider the following diagram: Isosceles triangle with equal sides of length 50 cm and base 2x. Perpendicular bisector is drawn from base to opposite vertex. Triangle has base angles of 40.8 degrees
     
    \[\begin{align*} \cos{(40.8^\circ)} &= \frac{x}{50} \\ x &= 37.85 \\ 2x &= 75.7 \end{align*}\]
     
  9. There is no solution provided for this question.
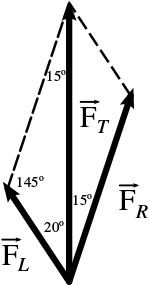
  10. Parallelogram of vectors F_L, F_R, and resultant F_T with two angles 145 and two 30. Angle 20 between F_L and F_T, angle 15 between F_L and F_T.

    Let \( \vec{F_R} \) be the force that the right-hand dog applies to the sled, \( \vec{F_L} \) be the force that the left-hand dog applies, and \( \vec{F_T} \) be the resultant.

    Let \( k \) be the ratio of the right-hand dog's force to the left-hand dog's force. Then \( \left \lvert F_R \right \rvert = k \cdot \left \lvert F_L \right \rvert \).

    The force diagram is shown to the right, oriented so that the direction of the sled's motion points along the vertical. Applying the Sine Law,

    \[\begin{align*} \frac{\left \lvert F_R \right \rvert}{\sin{(20^\circ)}} &= \frac{\left \lvert F_L \right \rvert}{\sin{(15^\circ)}} \\ \frac{k \cdot \left \lvert F_L \right \rvert}{\sin{(20^\circ)}} &= \frac{\left \lvert F_L \right \rvert}{\sin{(15^\circ)}} \\ k &= \frac{\sin{(20^\circ)}}{\sin{(15^\circ)}} \\ &= 1.32 \end{align*}\]

    Therefore, the dog on the right pulls with a force \( 1.32 \) times greater than the dog on the left.

     
  11. There is no solution provided for this question.
  12. Rectangular prism. Base rectangle length 15, width 12. Resultant from bottom right of base rectangle to top left of top rectangle. Resultant forms angle beta with base rectangle length, alpha with base rectangle width, delta with prism height.
    1. \[\begin{align*} \left \lvert F \right \rvert^2 &= 10^2 + 12^2 + 15^2 \\ \left \lvert F \right \rvert &= 21.7 \end{align*}\]
    2. \[ \cos{(\alpha)} = \frac{12}{21.7}, \cos{(\beta)} = \frac{15}{21.7}, \cos{(\delta)} = \frac{10}{21.7} \]\[ \alpha = 56.4^\circ, \beta = 46.3^\circ, \delta = 62.6^\circ \]