2. Functions, Graphs, and Limits
  3. Introduction to Calculus: Limits and Rates of Change

Partial Solutions


  1. There is no solution provided for this question.
    1. The distance is not changing at a constant rate. The average rate of change of the distance over the interval \( 0 \leq t \leq 0.64 \) is\[ \frac{8-10}{0.64-0} = \frac{-2}{0.64} = -3.125~\text{ m/s} \] while the average rate of change of the distance over the interval \( 0.64 \leq t \leq 0.90 \) is\[ \frac{6-8}{0.90-0.64} = \frac{-2}{0.26} \approx -7.692~\text{ m/s} \] In fact, since the time intervals are decreasing in length while the distance covered is remaining constant, the average rate of change is increasing in magnitude as time goes on.
    2. The average rate of change over the entire drop is \( \frac{0 - 10}{1.43 - 0} = \frac{-10}{1.43} \approx -6.993 \text{ m/s} \).
    3. By the argument from a) since the intervals of distance are constant while the time intervals are decreasing in length, the average rate of change is the largest (in magnitude) over the \( 5^{th} \) time interval \( 1.28 \leq t \leq 1.43 \). The average rate of change over this interval is \( \frac{0-2}{1.43 - 1.28} = \frac{-2}{0.15} = -13.\overline{3}~\text{m/s} \).
    4. The velocity after \( 1.11 \) seconds is the instantaneous rate of change of the distance at \( t =1.11 \). The average rate of change over the interval \( 0.9 \leq t \leq 1.11 \) is \( \frac{-2}{1.11-0.9} = -\frac{2}{0.21} \approx -9.524 \) and the average rate of change over the interval \( 1.11 \leq t \leq 1.28 \) is \( \frac{-2}{1.28-1.11} = -\frac{2}{0.17} \approx -11.765 \). We expect the instantaneous rate of change at \( t=1.11 \) to be somewhere in between these two values, so we average the values to get\[ v(1.11) \approx \frac{1}{2}(-9.524 + -11.765) = -10.645~\text{ m/s} \]
  3. There is no solution provided for this question.
    1. Let \( f(x) = 3-x^{2} \).
      \( x_{P} \) \( x_{Q} \) \( f(x_{P}) \) \( f(x_{Q}) \) \( m_{\text{secant}} = \dfrac{f(x_{Q}) - f(x_{P})}{x_{Q} - x_{P}} \)
      \( 1 \) \( 1.1 \) \( 2 \) \( 1.79 \) \( \frac{1.79 - 2}{1.1 - 1} = -2.1 \)
      \( 1 \) \( 1.01 \) \( 2 \) \( 1.9799 \) \( \frac{1.9799 - 2}{1.01 - 1} = -2.01 \)
      \( 1 \) \( 1.001 \) \( 2 \) \( 1.997999 \) \( \frac{1.997999 - 2}{1.001 - 1} = -2.001 \)
      \( 1 \) \( 0.999 \) \( 2 \) \( 2.001999 \) \( \frac{2.001999 - 2}{0.999 - 1} = -1.999 \)
      \( 1 \) \( 0.99 \) \( 2 \) \( 2.0199 \) \( \frac{2.0199 - 2}{0.99 - 1} = -1.99 \)
      \( 1 \) \( 0.9 \) \( 2 \) \( 2.19 \) \( \frac{2.19 - 2}{0.9 - 1} = -1.9 \)
      Estimating, \( m_{tangent} \approx \frac{1}{2}(-2.001 + -1.999) =-2 \).
    2. Let \( f(x) = 3^x + 1 \).
      \( x_{P} \) \( x_{Q} \) \( f(x_{P}) \) \( f(x_{Q}) \) \( m_{\text{secant}} = \dfrac{f(x_{Q}) - f(x_{P})}{x_{Q} - x_{P}} \)
      \( 2 \) \( 2.1 \) \( 10 \) \( 11.045 \ldots \) \( \frac{11.045 - 10}{2.1 - 2} \approx 10.451 \)
      \( 2 \) \( 2.01 \) \( 10 \) \( 10.099 \ldots \) \( \frac{10.099 - 10}{2.01 - 2} \approx 9.942 \)
      \( 2 \) \( 2.001 \) \( 10 \) \( 10.009 \ldots \) \( \frac{10.099 - 10}{2.001 - 2} \approx 9.893 \)
      \( 2 \) \( 1.999 \) \( 10 \) \( 9.990 \ldots \) \( \frac{9.990 - 10}{1.999 - 2} \approx 9.882 \)
      \( 2 \) \( 1.99 \) \( 10 \) \( 9.901 \ldots \) \( \frac{9.901 - 10}{1.99 - 2} \approx 9.833 \)
      \( 2 \) \( 1.9 \) \( 10 \) \( 9.063 \ldots \) \( \frac{9.063 - 10}{1.9 - 2} \approx 9.364 \)
      Estimating, \( m_{tangent} \approx \frac{1}{2}(9.893 + 9.882) = 9.8875 \).
    3. Let \( f(x) = \sqrt{2 + x} \).
      \( x_{P} \) \( x_{Q} \) \( f(x_{P}) \) \( f(x_{Q}) \) \( m_{\text{secant}} = \dfrac{f(x_{Q}) - f(x_{P})}{x_{Q} - x_{P}} \)
      \( 0 \) \( 0.1 \) \( \sqrt{2} \) \( 1.449 \ldots \) \( \frac{1.449 - \sqrt{2}}{0.1 - 0} \approx 0.3492 \)
      \( 0 \) \( 0.01 \) \( \sqrt{2} \) \( 1.417 \ldots \) \( \frac{1.417 - \sqrt{2}}{0.01 - 0} \approx 0.3531 \)
      \( 0 \) \( 0.001 \) \( \sqrt{2} \) \( 1.414 \ldots \) \( \frac{1.414 - \sqrt{2}}{0.001 - 0} \approx 0.3535 \)
      \( 0 \) \( -0.001 \) \( \sqrt{2} \) \( 1.413 \ldots \) \( \frac{1.413 - \sqrt{2}}{-0.001 - 0} \approx 0.3536 \)
      \( 0 \) \( -0.01 \) \( \sqrt{2} \) \( 1.410 \ldots \) \( \frac{1.410 - \sqrt{2}}{-0.01 - 0} \approx 0.3540 \)
      \( 0 \) \( -0.1 \) \( \sqrt{2} \) \( 1.378 \ldots \) \( \frac{1.378 - \sqrt{2}}{-0.1 - 0} \approx 0.3581 \)
      Estimating, \( m_{tangent} \approx \frac{1}{2}(0.3535 + 0.3536) = 0.35355 \).
    4. Let \( f(x) = \cos{(2x)} \).
      \( x_{P} \) \( x_{Q} \) \( f(x_{P}) \) \( f(x_{Q}) \) \( m_{\text{secant}} = \dfrac{f(x_{Q}) - f(x_{P})}{x_{Q} - x_{P}} \)
      \( \frac{\pi}{2} \) \( \frac{\pi}{2} + 0.1 \) \( -1 \) \( -0.9800 \ldots \) \( \approx 0.199 \)
      \( \frac{\pi}{2} \) \( \frac{\pi}{2} + 0.01 \) \( -1 \) \( -0.9998 \ldots \) \( \approx 0.020 \)
      \( \frac{\pi}{2} \) \( \frac{\pi}{2} + 0.001 \) \( -1 \) \( -0.9999 \ldots \) \( \approx 0.002 \)
      \( \frac{\pi}{2} \) \( \frac{\pi}{2} - 0.001 \) \( -1 \) \( -0.9999 \ldots \) \( \approx -0.002 \)
      \( \frac{\pi}{2} \) \( \frac{\pi}{2} - 0.01 \) \( -1 \) \( -0.9998 \ldots \) \( \approx -0.020 \)
      \( \frac{\pi}{2} \) \( \frac{\pi}{2} - 0.1 \) \( -1 \) \( -0.9800 \ldots \) \( \approx -0.199 \)
      Estimating, \( m_{tangent} \approx \frac{1}{2}(0.002 + -0.002) = 0 \).
  5. There is no solution provided for this question.
    1. \( a(2) = -10(2)^{2} + 60(2) = -10(4) + 120 = -40 + 120 = 80~\text{m} \). The altitude of the rock climber \( 2 \) hours after she begins her climb is \( 80~\text{m} \).
    2. \( a(3) = -10(3)^{2} + 60(3) = -10(9) + 180 = -90 + 180 = 90~\text{m} \). The altitude of the rock climber \( 2 \) hours after she begins her climb is \( 90~\text{m} \).
    3. The average rate of change of the altitude of the rock climber is given by\[ \frac{a(3) - a(2)}{3-2} = \frac{90-80}{1} = 10~\text{m/h} \] The average rate of change of the altitude of the rock climber between \( 2 \) and \( 3 \) hours after she begins her climb is \( 10~\text{m/h} \).
    4. The instantaneous rate of change of the climber's altitude at \(t = 3\) can be calculated as follows:\[ m_{tangent} = \lim_{h \rightarrow 0} \frac{a(3+ h) - a(3)}{(3+h) - 3}\] From part b), \( a(3) \) is known, and\[ \begin{align*} a(3+ h) &= -10(3+h)^{2}+60(3+h) \\ &= -10(9 + 6h + h^{2}) + 180 + 60h \\ &= -90 - 60h - 10h^{2} + 180 + 60h \\ &= 90 - 10h^{2} \\ \end{align*} \] Substituting this expression into the formula for the slope of the tangent,\[ \begin{align*} m_{tangent} &= \lim_{h \rightarrow 0} \frac{a(3+ h) - a(3)}{(3+h) - 3}\\ &= \lim_{h \rightarrow 0} \frac{\left[90- 10h^{2}\right] - 90}{h}\\ &= \lim_{h \rightarrow 0} \frac{-10h^{2}}{h} \\ &= \lim_{h \rightarrow 0} -10 h \\ &= 0 \end{align*} \]Therefore, the instantaneous rate of change of the altitude of the rock climber \( 3 \) hours after she begins her climb is \( 0~\text{m/h} \).
    5. An instantaneous rate of change of \( 0 \) indicates that the rock climber stops her ascent at \( t = 3 \) and then starts descending.
  7. There is no solution provided for this question.
    1. Graphing the data, Graph of points given in question.
    2. No, the temperature of the water is not increasing at a constant rate. For example, the average rate of change between \( 0 \) and \( 1 \) minute is \( \frac{8 - 6}{1 - 0} = 2~^\circ\text{C/min} \), and the average rate of change between \( 1 \) and \( 4 \) minutes is \( \frac{10 - 8}{4 - 1} = \frac{2}{3}~^\circ\text{C/min} \).
    3. The average rate of change between \( 4 \) and \( 9 \) minutes is the slope of the secant joining the points \( (4, 10) \) and \( (9, 12) \). This value is \( \frac{12-10}{9-4} = \frac{2}{5}~^\circ\text{C/min} \). Similarly, the average rate of change between \( 9 \) and \( 16 \) minutes is \( \frac{14-12}{16-9} = \frac{2}{7}~^\circ\text{C/min} \).
    4. From the following table showing the average rates of change over each time interval:
      \( \text{Interval}~ \text{(in min)} \) \( \text{Average rate of change}~(\, ^\circ \text{C/min}) \)
      \( 0 \leq t \leq 1 \) \( \frac{8-6}{1-0} = \frac{2}{1} = 2 \)
      \( 1 \leq t \leq 4 \) \( \frac{10-8}{4-1} = \frac{2}{3} = 0.\overline{6} \)
      \( 4 \leq t \leq 9 \) \( \frac{12-10}{9-4} = \frac{2}{5} = 0.4 \)
      \( 9 \leq t \leq 16 \) \( \frac{14-12}{16-9} = \frac{2}{7} \approx 0.2857... \)
      \( 16 \leq t \leq 25 \) \( \frac{16-14}{25-16} = \frac{2}{9} = 0.\overline{2} \)
      \( 25 \leq t \leq 36 \) \( \frac{18-164}{36-25} = \frac{2}{11} = 0.\overline{18} \)
      the highest average rate of change is \( 2~^\circ\text{C/min} \) and it occurs between \( 0 \) and \( 1 \) minute. Looking at the graph, observe that if secant lines are drawn between adjacent data points, the line with the steepest slope will be the line joining the first two data points.
      1. The average rate of change between \( 4 \) and \( 9 \) minutes is \(\frac{2}{5}~^\circ\text{C/min}\) and the average rate of change between \( 9 \) and \( 16 \) minutes is \(\frac{2}{7}~^\circ\text{C/min}\). The instantaneous rate of change after \( 9 \) minutes is likely somewhere in between these values. The average of these two values is\[ \frac{1}{2} \left(\frac{2}{5} + \frac{2}{7}\right) = \frac{1}{2} \left(\frac{24}{35}\right) \approx 0.34~^\circ\text{C/min} \] so an estimate for the instantaneous rate of change at \(t=9\) is approximately \(0.34~^\circ\text{C/min}\).
      2. Now draw a smooth curve through the points. Then, we draw a tangent line at the point \((9, 12)\) and approximate the slope of this tangent. From the graph, the slope of the tangent is approximately \(\frac{1}{3}\). Smooth curve drawn through point plot in 8a; tangent line drawn to curve at (9, 12)
      1. SSince \(T(0) = 6\), we have \(T(0)=a\sqrt{0} +b = b = 6\) . So \(T(t) = a\sqrt{t} +6\). Since \(T(1) = 8\), we have \(T(1) = a\sqrt{1} +6 = a + 6\) and so \( a = 2 \). Therefore, the only possible formula is \(T(t) = 2\sqrt{t} +6\). A quick check will confirm that the remaining \( 5 \) data points also satisfy this formula.
      2. Consider the points \(P~(9,T(9))\) and \(Q~(9+h, T(9+h))\). Then, the slope of the tangent line at \(t=9\) can be calculated as follows: \[ \begin{align*} m_{tangent} &= \lim_{h \rightarrow 0} m_{secant}\\ &= \lim_{h \rightarrow 0} \frac{T(9+h) - T(9)}{(9+h) - 9} \\ &= \lim_{h \rightarrow 0} \frac{\left(2 \sqrt{9+h} + 6\right) - \left(2 \sqrt{9}+6\right)}{h}\\ &= \lim_{h \rightarrow 0} \frac{\left(2 \sqrt{9+h} + 6\right) - \left(12\right)}{h}\\ &= \lim_{h \rightarrow 0} \frac{2 \sqrt{9+h} -6}{h} ~ \left(\frac{2 \sqrt{9+h} + 6}{2 \sqrt{9+h} + 6}\right)\\ &= \lim_{h \rightarrow 0} \frac{4(9+h) - 36}{h\left(2 \sqrt{9+h}+6\right)}\\ &= \lim_{h \rightarrow 0} \frac{4h}{h\left(2 \sqrt{9+h}+6\right)}\\ &= \lim_{h \rightarrow 0} \frac{4}{\left(2 \sqrt{9+h}+6\right)}\\ &= \frac{4}{\left(2 \sqrt{9+0}+6\right)}\\ &=\frac{4}{\left(2 (3)+6\right)}\\ &= \frac{4}{12} \\ &= \frac{1}{3}\\ \end{align*} \]
  9. There is no solution provided for this question.

  10. Let \( y \) represent the length of the man's shadow in metres. Let \(x\) represent the distance between the man and the base of the streetlight. Note that the quantities \(x\) and \(y\) are both changing with respect to time, as the man walks, and so we have \(x = x(t)\) and \(y = y(t)\).

    In the diagram below, the man's head is located at \( H \), his feet at \( P \), the lamp at \( L \), the base of the lamp at \( O \), and the tip of his shadow at \( G \). Let \( OP = x \) and \( PG = y \). 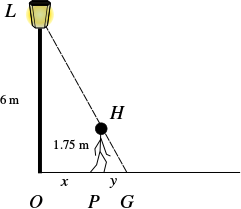Image of situation described in solution.

    Note that \( \triangle{HGP} \sim \triangle{LGO} \), so

    \[ \begin{align*} \dfrac{OG}{LO} &= \dfrac{PG}{HP} \\ \dfrac{x+y}{6} &= \dfrac{y}{1.75} \\ 4.25y &= 1.75x \\ y &= \frac{175}{425}x \\ &= \frac{7}{17}x \end{align*} \]

    The rate at which the man is walking away, at time \(t\), is the instantaneous rate of change of the distance between the man and the streetlight at time \(t\). This is given by the expression

    \[ \lim_{h \rightarrow 0} \frac{x(t+h) - x(t)}{(t+h)-t} =\lim_{h \rightarrow 0}\frac{x(t+h) - x(t)}{h} \]

    Similarly, the instantaneous rate of change of the length of the shadow is given by

    \[\lim_{h \rightarrow 0} \frac{y(t+h) - y(t)}{(t+h)-t}= \lim_{h \rightarrow 0} \frac{y(t+h) - y(t)}{h}.\]Since \(y = \dfrac{7}{17}{x}\), we have \(y(t+h)= \dfrac{7}{17}x(t+h)\) and \(y(t) = \dfrac{7}{17}x(t)\), and so\[\lim_{h \rightarrow 0} \frac{y(t+h) - y(t)}{h} = \lim_{h \rightarrow 0}\frac{\frac{7}{17}x(t+h) - \frac{7}{17}x(t)}{h} =\lim_{h \rightarrow 0} \frac{7}{17}\frac{x(t+h) - x(t)}{h} = \frac{7}{17}\lim_{h \rightarrow 0} \frac{x(t+h) - x(t)}{h} \]

    Therefore, the rate at which the length of the shadow is increasing is \(\dfrac{7}{17}\) times the rate at which the man is walking away from the streetlight.