Lesson Part 1
Introduction
Optimization is one of the most common and important uses of calculus as it offers us concrete evidence to make well-informed decisions.
Using calculus to identify a function's extreme values—the maximums and the minimum values of a function—has many practical applications to real life.
For example, suppose you wanted to build a wooden deck in your backyard but had a limited budget for purchasing the materials.
Calculus can help you determine the best dimensions for the deck that will allow you to stay on budget while maximizing the area of your deck space.
In This Module
- We will work through a variety of optimization problems to see the methods we can use to solve them.
Let's begin with the following example.
Examples
Example 1
At a local lake, a lifeguard has \(500\) meters of buoyant rope to mark the boundary lines of a rectangular swimming area. She does not need a boundary line along the side of the swimming area where there is beach. What are the dimensions of the largest swimming area that this lifeguard can make?
Solution
Before beginning to answer this problem, let's break down the wording that's in the question. We are told that the lifeguard has \(500\) metres of buoyant rope. What does this tell us about this swimming area? Well the buoyant rope will be used to mark the perimeter of the swimming area. So we know that the perimeter—only on three sides though, since one side will be the beach—the three sided perimeter of the rectangular swimming area must be \(500\) metres.
Also, we know that the lifeguard is trying to maximize the area of the swimming area. Since the swimming area is a rectangle, we will use the formula \(A=lw\) to calculate the area of the rectangle.
Now that we've broken down the problem into the given information, let's begin by sketching a diagram to match this problem.
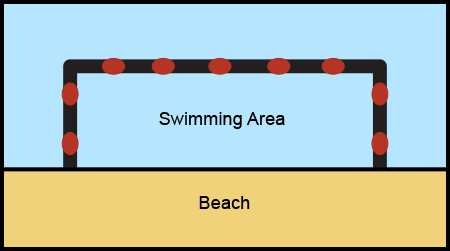
The rectangular swimming area has four sides. Along three of the sides is the boundary rope marking off the swimming area. The fourth side is the beach. The lifeguard can modify the swimming area by making the width longer, which causes the length of the swimming area to shorten, or by making the length longer, which causes the width of the swimming area to shorten, as shown in the diagram.
As the lifeguard changes the length and width of the rectangular boundary, the swimming area changes in size.
Since we don't know the length or the width of the maximized swimming area, these will be our two unknowns used in this problem.
So, let's label the length, \(l\), and width, \(w\), of the swimming area on the diagram.
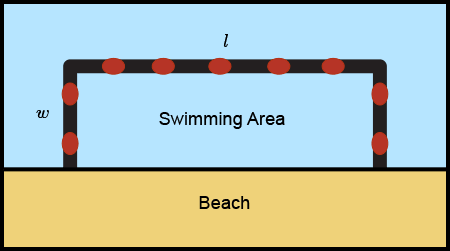
Since the boundary rope will be used along two widths and one length of the swimming area, and the lifeguard has only \(500\) meters of rope, we know that
\[l+2w=500\]
This equation allows us to relate our two variables together. Let's solve for \(l\) in terms of \(w\).
\(l+2w=500\), which implies that \(l=500-2w\).
We now have an equation that relates our two variables directly. Before moving on, we need to consider the possible values for \(l\) and \(w\).
First of all, since we only have \(500\) metres of rope, neither \(l\) nor \(w\) could exceed \(500\) metres. Also, since we have two sections of width making up our swimming area, we know that the width cannot exceed half of the length of the rope, which implies that the width must be less than or equal to \(250\) meters. Formally, we have note this as follows:
Note: We assume that both \(l\) and \(w\) are non-negative, so to make a swimming area with this rope, \(0\leq w\leq250\) and \(0\leq l\leq500\).
That is, we know that the width of the swimming area must be between \(0\) and \(250\) metres, and the length of our swimming area must be between \(0\) and \(500\) metres.
Since the lifeguard wants to maximize the swimming area, \(A\), we will use the derivative to determine the maximum value of the function
\[A=lw\]
However, \(A\) is expressed in terms of two variables—\(l\) and \(w\)—and we do not know how to differentiate an expression where one variable is related to two other variables. So before differentiating, we need to express the area, \(A\), in terms of only one variable.
This can be achieved by substituting \(l=500-2w\) into \(A=lw\) giving a function for the area \(A(w)\) in terms of the width \(w\). Remember to state the restriction.
\[\begin{align*}A(w) & =(500-2w)w, \quad\text{ for } 0\leq w\leq250 \\ & =500w-2w^2 \end{align*}\]
We now have a polynomial function that relates the area of the swimming area to the width of the swimming area.
Recall every polynomial function is differentiable on its domain. Since \(A(w)\) is a polynomial, which tells us that \(A'(w)\) exists for all \(w\), the extreme value theorem tells us that a maximum and/or minimum value will occur when \(A'(w)=0\) or at the endpoints of the interval \(0\leq w\leq250\).
So we will begin by differentiating the area function to determine the values of \(w\)—where \(A'(w) = 0\)—and then we will check the area at that value with the area at the end points of the interval to determine the maximum swimming area.
Differentiating the area function, we have
\[A'(w)=500-4w\]
Let's now solve for \(w\) when \(A'(w)=0\).
\[\begin{align*}0 & =500-4w \\ w & =125 \text{ m}\end{align*}\]
Now let's compare the values of the area when the end points of the interval for \(w\) end when \(w= 125\) m.
When \(w=0\), the area of the rectangular swimming area is \(0\).
\[A(0) = =500(0)-2(0)^2=0\]
When \(w= 250\), the area of the rectangular swimming area is also \(0\).
\[A(250)=500(250)-2(250)^2=0\]
But when \(w= 125\) m, the area of the rectangular swimming area is \(31~250\) m\(^2\).
\[A(125) = 500(125)-2(125)^2=31\ 250 \text{ m}^2\]
The maximum swimming area occurs when \(w=125\) m.
We can find the length, \(l\), of the swimming area by substituting \(w=125\) m into the function \(l=500-2w\). Remember, this is the equation that relates the length to the width of the swimming area.
\[\begin{align*} l & =500-2(125) \\ & =250 \text{ m} \end{align*}\]
Thus, the rectangular swimming area's dimensions should be \(125\) metres wide and \(250\) metres long to have an optimal area.
Lesson Part 2
Examples
Let's now try another example. You'll see some common approaches to solving this optimization problem, even though the problem itself is quite different from the swimming area problem we just solved.
Example 2
Local farmers wish to sell apple cider in cylindrical containers. They need you to design a container that will hold \(432\) mL of apple cider and minimize the cost of the metal used to manufacture the container. Determine the dimensions of this container.
Solution
Again, before we begin an answer to this problem, let's deconstruct the wording of the problem. We know that the apple cider container must hold \(432\) mL. This is the volume of the container that we must create. Also, we're asked to minimize the cost of the metal used to manufacture the container.
Well, the metal makes up the surface area of the container, so we need to minimize the surface area for a volume of a cylindrical container that will hold \(432\) mL of apple cider.
We begin by sketching a diagram to match this problem.
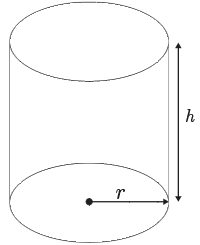
The two dimensions of the cylinder that we can modify are the height and radius of the container. As the height increases, the radius decreases. As the radius increases, the height decreases.
Since these two values are unknown for the optimal dimensions of the container, let's label our unknowns on the diagram, \(h\) for height and \(r\) for radius.
The apple cider container must hold \(432\) mL of apple cider, which we take to be equivalent to \(432\) cm\(^3\). This is the volume of the container. Recall that the volume formula for a cylindrical container is \(V=\pi r^2h\). Therefore, we know that
\[V=\pi r^2h=432 \text{ cm}^3\]
We are assuming that \(432\) cubic centimetres is equal to \(432\) millilitres of apple cider.
Now, this equation allows us to relate our two variables together. Let's solve for height, in this case, since solving for height is much easier than solving for radius in this equation.
\[h=\dfrac{432}{\pi r^2} \text{ cm}\]
We now have an equation that relates the two variables together.
Note that to make a cylinder with volume \(432\) cm\(^3\), it must have dimensions \(h,r \gt 0\).
To minimize the cost of constructing this container, we must minimize the amount of metal used to make the container. In other words, we must minimize the surface area of the container.
The surface area of a cylindrical container is calculated by using the formula, \(A= 2 \pi r^2\), which is the area of the top and bottom of the container, plus \(2 \pi r h\), which is the lateral surface area of the container.
Therefore, we want the minimum value of the function \(A=2\pi r^2 +2\pi rh\), which is the sum of the surface areas of the top, bottom, and sides of the container.
Much like in our first example, we see that the area of the container is related to two variables, radius and height. Before differentiating, we need to express the area, \(A\), in terms of only one variable.
This can be achieved by substituting \(h=\dfrac{432}{\pi r^2}\) into \(A=2\pi r^2 +2\pi rh\) giving a function for the area, \(A(r)\), in terms of the radius, \(r\).
\[\begin{align*}A(r) & =2\pi r^2 +2\pi r\left(\dfrac{432}{\pi r^2}\right), \quad \text{ for }r \gt 0 \end{align*}\]
First, to maximize this area formula, we find the critical points of \(A(r)\).
Differentiating the area function, we have
\[\begin{align*}A'(r) & =4\pi r -864(r^{-2}) \\ & =4\pi r -\dfrac{864}{r^2} \\ & =\dfrac{4\pi r^3 -864} {r^2}\end{align*}\]
Notice we rewrote the equation to have a positive exponent on \(r\) and combined the terms so that we have a common denominator.
Let's now solve for \(r\) when \(A'(r)=0\). This will give us the critical points. Essentially, we need to solve for when the numerator is equal to \(0\).
\[\begin{align*} 0& =\dfrac{4\pi r^3 -864} {r^2}\\ 0& =4\pi r^3 -864, \quad \text{ since } r \neq 0 \\ r& = \dfrac{6}{\sqrt[3]{\pi}} \approx 4.10 \ \text{cm} \end{align*}\]
Again, recall that \(r\) must be greater than \(0\).
We now need to find the value of the area when \(r=6\pi^{- \frac{1}{3}}\). It's probably easier in this case to substitute \(r=6\pi^{- \frac{1}{3}}\) than writing \(\dfrac{6}{\sqrt[3]{\pi}}\), but I will let you make that decision for yourself.
\[\begin{align*}A(r) & =2\pi \left(6\pi^{- \frac{1}{3}}\right)^2 +864\left(6\pi^{- \frac{1}{3}}\right)^{-1} \\ & =72\pi^{\frac{1}{3}}+144\pi^{\frac{1}{3}} \\ & =216\pi^{\frac{1}{3}} \approx 316.4 \text{ cm}^2\end{align*}\]
In our last example, we tested not only the critical points of the function, we also tested the endpoints on the interval of the width.
Since the domain of \(A(r)=2\pi r^2 +864r^{-1}=\dfrac{2\pi r^3 +864}{r}\) is \((0,+\infty)\), we cannot substitute the endpoints into the function to determine if a minimum exists at an endpoint.
Instead, we will apply the first derivative test. Recall that \(A'( r)= \dfrac{4\pi r^3-864}{r^2}\) and observe that for
\[r \lt \dfrac{6}{\sqrt[3]{\pi}}, \: r^3 \lt \dfrac{216}{\pi}\]
and hence
\[4\pi r^3 \lt 864\]
so \(A'(r) \lt 0\) meaning that \(A(r)\) is decreasing.
Similarly, for
\[r \gt \dfrac{6}{\sqrt[3]{\pi}} , \: 4\pi r^3 \gt 864\]
so \(A'(r)>0\) meaning that \(A(r)\) is increasing.
So before our value of \(r\), \(A(r)\) is decreasing, and after our value of \(r\), \(A(r)\) is increasing, which means an absolute minimum must exist at
\[r=\dfrac{6}{\sqrt[3]{\pi}}\approx 4.10 \text{ cm}\]
We can see this absolute minimum value by graphing the function of \(A(r) = 2\pi r^2 + \dfrac{864}{r}\).
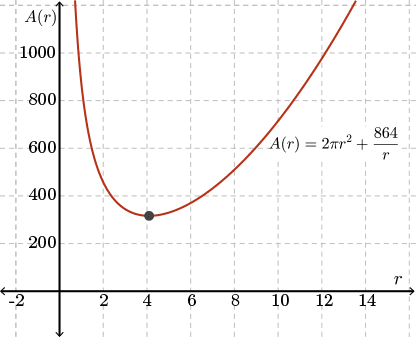
Now, let's find the height, \(h\), of the apple cider container by substituting the minimum value \(r=\dfrac{6}{\sqrt[3]{\pi}}\) into the function \(h=\dfrac{432}{\pi r^2}\).
\[\begin{align*}h & =\dfrac{432}{\pi \left(6\pi^{-\frac{1}{3}}\right)^2} \\ & =\dfrac{12}{\sqrt[3]{\pi}} \\ & \approx8.19 \text{ cm}\end{align*}\]
Thus, the apple cider container should have a radius of \(\dfrac{6}{\sqrt[3]{\pi}}\approx 4.10\) cm and a height of \(\dfrac{12}{\sqrt[3]{\pi}}\approx 8.19\) cm to be at an optimal cost.
Special Note:
Although we have found the dimensions of an apple cider can that has the best dimensions to optimize costs, manufacturers combine this knowledge with marketing strategies to determine a design that is also “practical” and/or aesthetically pleasing.
It is important to ask the question: Would a person be comfortable holding onto a can that has the same diameter as height, like the can found in this example?
Picture what that container would look like and feel like in your head. Would this ultimately be the best design for the container?
Lesson Part 3
Helpful Strategies for Solving Optimization Problems
Now that we have worked through two examples of optimization problems, you may have spotted some themes that are common to the solution to both problems. Here are some helpful strategies for solving optimization problems.
Optimization problems can be challenging. Usually, the difficulty lies in understanding and interpreting the problem and then getting started. The following steps can help with this process.
- Thoroughly Read and Understand the Problem
The first step to solving any problem is to read the problem thoroughly to identify what information has been given and understand what is being asked.
Make a list of the given quantities in the problem and the unknown quantity we wish to optimize.
Lastly, look for possible restrictions on variables or identify unique conditions.
- Sketch a Diagram
If the context of the problem can be represented by a diagram, then make one.
Label the known and unknown dimensions on the diagram.
- Introduce Notation
Define symbols given to variables; for example, \(A\) represents the surface area of the container.
After defining the symbols you will use for your unknowns, list any restrictions on the variables and state their units. In the case of the apple cider container, we needed to convert the unit millilitres into the unit cubic centimetres.
- Relate the Known and Unknown Quantities
Consider the given information and the quantity to be optimized.
Often, the wording within an optimization problem will lead you to identify a function that relates the optimized quantity with other variables given in the problem. It will also lead you to an equation that relates unknown variables together so that the optimized quantity can be expressed with respect to only one variable.
In example 1, the problem asked to optimize the swimming area, for which we used the formula \(A=lw\).
Since the swimming area, \(A\), was related to two variables, \(l\) and \(w\), we needed an equation that related the length, \(l\), of the swimming area to its width, \(w\).
Since we knew that the lifeguard had only \(500\) m of rope (i.e., the perimeter of the three sides of the rectangle was \(500\) m), we related the length and width by the equation \(l+2w=500\).
When you consider the information given by the problem, ask yourself: “Is there a known function that relates these variables to one another?” Sometimes we will use a known function, like the area of a rectangle. However, in other cases, you may have to ask yourself, “Can you create a function that describes the optimized quantity using the other given information?”
Here, you may need to use your creative mathematical modelling skills.
Once you have related the optimized quantity to another variable(s) given in the problem, identify whether the optimized quantity is related to one or more than one variable.
If the optimized quantity is related to more than one variable, you may need to determine an equation that relates these variables to one another.
- Apply the Extreme Value Theorem or the First Derivative Test to Determine the Absolute Maximum or Minimum Value
Determine where the function, \(f(x)\), to be optimized has any critical points by finding all points within the relevant interval where \(f'(x)=0\) or \(f'(x)\) is undefined.
Once these values of \(x\) are identified, we then determine the value of \(f(x)\) at each of these points.
Next, if the interval is closed, say \(a \leq x \leq b\), determine \(f(a)\) and \(f(b)\) and compare these values to those of \(f\) at any critical point in \(a \lt x \lt b\) in order to choose the desired absolute maximum or minimum.
If the interval is open, rather than using the extreme value theorem, use the first derivative or second derivative test to determine the nature of any critical points (like we did in example 2). Again, once we have determined the position of the critical points, we substitute those critical points into our function to determine its value, and then select the desired absolute maximum or minimum.
Lesson Part 4
Examples
So now that we have some helpful strategies as to how to solve an optimization problem, let's try a more challenging question.
Challenge Question
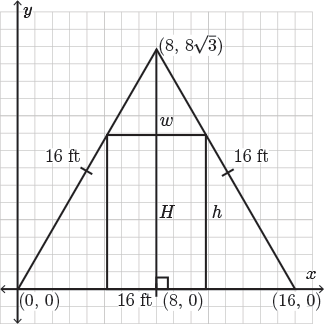
The roof line of the third floor of a house is in the shape of an equilateral triangle, with each side measuring \(16\) feet. The home owners wish to install a rectangular glass door at one end of the roof. Determine the maximum area of the door that could be installed.
Solution
Let's break down the wording of this problem. We know that the roofline makes an equilateral triangle. So let's begin by sketching a diagram of this roofline. We also know that the length of each side of the equilateral triangle is \(16\) feet. Let's add this dimension to our diagram.
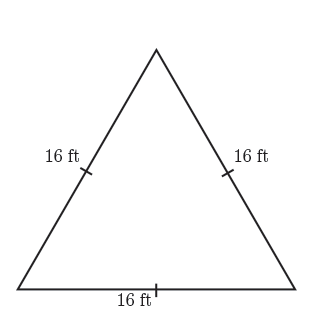
Finally, we're asked to maximize the area of a rectangular door that could be installed within the equilateral triangle. We do not know the height or width of this door. However, since we wish to maximize the area of a rectangular door that can be inscribed within the equilateral triangle, we know that the vertices of this rectangular door will occur along the edges of the equilateral triangle.
Now, the rectangular door's area can be modified by making the height, \(h\), taller or the width, \(w\), wider, which will change the area of the door. So the height of the door and the width of the door are two unknown quantities that we can use to solve this problem. Let's label these unknowns on the diagram.
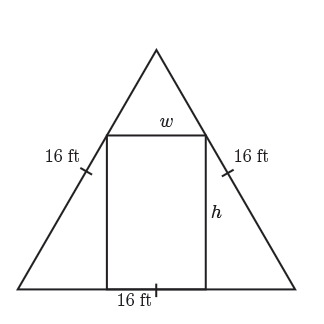
The length of each side of the equilateral triangle is known. Therefore, the area of the equilateral triangle can be found. This is one possible known quantity that we may need to use to relate our two variables together.
Another possible way that we could relate our two variables together is by applying the Pythagorean theorem. If we draw a vertical line from the top vertex of the equilateral triangle down to its base, labelled \(H\), we have a right triangle. Since two sides of this right-angled triangle are known, the hypotenuse is \(16\) and the leg on the base is \(\frac{16}{2} =8\). The quantity \(H\) can be calculated using the Pythagorean theorem.
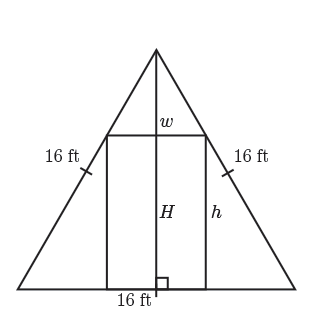
Here we have another known quantity of the equilateral triangle that may help us relate our two variables together later in the problem. This problem is a bit more challenging than the first two problems that we solved. Here, we do not have a known formula that relates our two quantities together.
Here's a helpful strategy. Let's use the methods of analytic geometry to help us solve this problem, meaning that we're going to take the equilateral triangle and place it onto a grid. Since the base length of the equilateral triangle is \(16\) feet, we place one vertex of the base at the origin, \((0,0)\). So the bottom right vertex of the equilateral triangle will be located at the point \((16, 0)\).
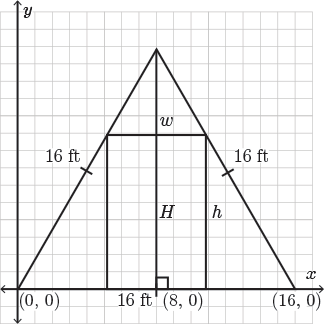
Applying the Pythagorean theorem, we can calculate the height of the equilateral triangle. Let's do that now to determine the coordinates of the top vertex of the equilateral triangle.
\[H=\sqrt{16^2-8^2}=\sqrt{192}=8\sqrt{3} \text{ ft}\]
Therefore, the top vertex of the triangle will occur at the point \((8, 8\sqrt{3})\).
Now let's focus on the top left vertex of the rectangular door. We know that the position of this vertex will be somewhere along the side length of the equilateral triangle. Suppose that the top left vertex of the rectangle is point \((x,y)\).
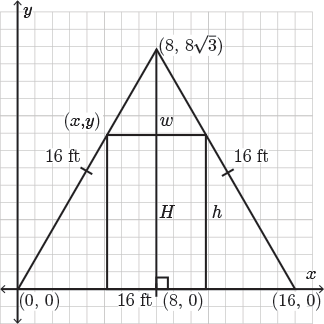
As we drag this point along the edge of the equilateral triangle, we see that we modify the area of the rectangular door inscribed within the equilateral triangle. We now have four unknown dimensions in this diagram. Before moving on, let's restrict these variables.
Since the height of the door cannot exceed the height of the equilateral triangle, we know that the height of the rectangular door must be \(0 \leq h \leq 8\sqrt{3}\).
Also, we know that the width of the door cannot exceed the width of the equilateral triangle. So, \(0 \leq w \leq 16\).
Since the point \((x, y)\) lies along the left edge of the equilateral triangle, \(0 \leq x \leq 8\) and \(0 \leq y \leq 8\sqrt{3}\). All four of our dimensions are measured in feet.
The coordinates of the point \((x,\ y)\) are related to the dimensions of the rectangular door.
The height of the door is equal to \(y\) (i.e., \(h=y\)).
The \(x\)-coordinate of this point takes us to the left side of the rectangular door. Since half of the base length of the equilateral triangle is \(8\), we know that half of the width of the door is equal to \(8-x\).
Thus, the total width of the door is \(w=2(8-x)=16-2x\) ft.
Now, how do we relate \(x\) to \(y\)?
The left side of the equilateral triangle is a line segment. To determine the equation on this line segment, we need the slope of this line segment and we need a point on this line segment.
We can calculate the slope of this line segment by using the top vertex of the equilateral triangle and the bottom left vertex of the equilateral triangle. In other words, we will use the point \((8, 8 \sqrt{3})\) and the point \((0, 0)\) to calculate its slope.
The slope of this line segment is \(m=\dfrac{8\sqrt{3}-0}{8-0}=\sqrt{3}\).
Since the \(y\)-intercept of this line is the origin \((0, 0)\), we can substitute the \(y\)-intercept, \(0\), and the slope, \(\sqrt{3}\), into the equation \(y=mx+ b\), which gives the equation of the line segment, which is the left side edge of the equilateral triangle. Therefore, we get \(y=\sqrt{3}x\).
So, we now have an equation that relates \(x\) to \(y\). That is, in terms of \(x\), \(y=\sqrt{3}x\) and, since \(y\) is the same as the height of the rectangular door, \(h=y=\sqrt{3}x\).
So we now can relate the area of the door in terms of the \(x\)-coordinate of that top left vertex.
The function representing the area of the rectangular door, \(A(x)\), is equal to the width of the door, \(16 - 2x\), times the height of the door, \(\sqrt{3} x\). That is,
\[A(x)=(16-2x)(\sqrt{3}x)=16\sqrt{3}x-2\sqrt{3}x^2\]
Differentiating this equation to find any critical points for this function, we have
\[A'(x)=16\sqrt{3}-4\sqrt{3}x\]
The maximum area of the door may occur when \(A'(x)=0\). Solving for \(x\) in this equation, we have
\[\begin{align*}0 & =16\sqrt{3}-4\sqrt{3}x \\ x & =\dfrac{16\sqrt{3}}{4\sqrt{3}} \\ & =4 \text{ ft}\end{align*}\]
Let's now find the value of the area when \(x=4\). Substituting \(x=4\) into \(A(x)=(16-2x)(\sqrt{3}x)\), gives
\[\begin{align*} A(4) & =[16-2(4)][\sqrt{3}(4)] \\ & =32\sqrt{3}\approx 55.43 \text{ ft}^2\end{align*}\]
Now, recall that the extreme value theorem requires us to check the endpoints of the interval of \(x\) to ensure that the area that we find is the absolute maximum area At the endpoints of the interval (i.e., when \(x=0\) or when \(x=8\)), the area of the rectangular door would be \(0\).
Thus, the maximum area of the door is \(32\sqrt{3}\approx 55.43\) ft\(^2\).
Note that this problem can also be solved using similar triangles. After we draw a perpendicular from the top vertex of the equilateral triangle to the base, we form many similar triangles in the diagram. You can locate three similar triangles in the diagram and use the fact that corresponding sides of similar triangles are proportional to relate the quantities \(w\) and \(h\), the width and height of the opening. This alternate proof is left as an exercise.