Alternative Format


Try This

If you have two fractions, how can you tell which one is larger? Sometimes you can tell just by looking at the fractions. And other times, you need to actually crunch some numbers.

Lesson Goal

  • Explore how fractions can be compared using common denominators or common numerators.

Try This!

First, I'd like you to take a moment and try the following question. The reasoning from each part of these questions actually introduces our understanding of how fractions that have like numerators or like denominators work.

Consider the following two cases:

Choice 1

Choice 1: three small squares on the left and three large squares on the right.

Choice 2

Choice 2: three small squares on the left and five small squares on the right.

  1. Which picture represents a larger area?
  2. Can you explain your answer without doing any calculations?

Think about this problem, then move on to the next part of the lesson.


Using "Greater Than" and "Less Than" Symbols

Using > and <

You should be familiar with how to use the equals sign (\( = \)) to show that two numbers are the same.

It is also helpful to show whether a number is greater than or less than another number.

To do this, we need two additional symbols that are the

  • greater than sign (\( \gt \)), and
  • less than sign (\( \lt \)).

Now, both a greater than and the less than signs each look like a V on their side.

For each sign, the "small" end always points towards the smaller number.

\( \class{hl1}{2} \lt 3 \)

or

\( 3 \gt \class{hl1}{2} \)

Example 1

Use \( \lt \) or \( \gt \) to compare \( 11 \) and \( 6 \)

If we write \(11\) first, then we need to use the greater than sign before writing \(6\).

\(11 \gt 6\)

This statement reads that, "\( 11 \) is greater than \( 6 \)."

Alternatively, if we wanted to write \(6\) first, then we would need to use the less than sign before writing the numeral \(11\).

\(6 \gt 11\)

This would then read that, "\( 6 \) is greater than \( 11 \)."

Notice how the symbol always "points" towards the smaller number.

Example 2

We have previously looked at the number line. One important feature of the number line is that the numbers are ordered from least to greatest when read from left to right. 

We can use \( \gt \) and \( \lt \) as a way to communicate specific information from the number line.

Use the following number line to write a true statement that uses the greater than sign.

Choose two fractions and write a true statement.

On our number line, we have four fractions. Now, we could choose any two of the fractions to write our statement. I'm going to choose \(\dfrac{5}{13}\) and \(\dfrac{2}{9}\).

What we notice is that \(\dfrac{5}{13}\) is farther to the right on the number line than \(\dfrac{2}{9}\) is.

A number line from 0 to 1 with fractions 2 over 9, 3 over 8, 5 over 13, and 4 over 7 listed from left to right.

This means that \(\dfrac{5}{13}\) is greater than \(\dfrac{2}{9}\), we can write this as:

\( \dfrac{5}{13} \gt \dfrac{2}{9} \)

I'm going to give you an opportunity to try some problems on your own. Always remember that when using the number line, the larger numbers are found farther right and the smaller numbers are found farther left.

Check Your Understanding 1

Question (Version 1)

Use \(\lt\) or \(\gt\) to compare the two fractions.

\(\dfrac{11}{13}~\boxed{\phantom \square}~\dfrac{3}{20}\)

The number line is provided to help you. 

A number line between 0 and 1. The fractions three-twentieths, three-elevenths, and eight-twentieths are plotted in order closer to zero. On the right, near 1, eleven-thirteenths is plotted.
Created with GeoGebra. Author: University of Waterloo. CC BY-NC-SA 4.0. http://ggbm.at/tRrNV5QW

Answer (Version 1)

\(\dfrac{11}{13}~\gt ~ \dfrac{3}{20}\)

Feedback (Version 1)

\(\dfrac{11}{13}\) is greater than \(\dfrac{3}{20}\) because \(\dfrac{11}{13}\) is farther to the right on the number line. 

Question (Version 2)

Use \(\lt\) or \(\gt\) to compare the two fractions.

\(\dfrac{2}{20}~\boxed{\phantom \square}~\dfrac{3}{14}\)

The number line is provided to help you. 

A number line between 0 and 1. The fractions two-twentieths, and three-fourteenths are plotted in order closer to zero. In the middle, the fraction eleven-twenty-fourths is plotted. On the right, near 1, five-sixths is plotted.
Created with GeoGebra. Author: University of Waterloo. CC BY-NC-SA 4.0. http://ggbm.at/tRrNV5QW

Answer (Version 2)

\(\dfrac{2}{20}~\lt ~ \dfrac{3}{14}\)

Feedback (Version 2)

\(\dfrac{2}{20}\) is less than \(\dfrac{3}{14}\) because \(\dfrac{2}{20}\) is farther to the left on the number line. 


Fractions with Like Denominators

Example 3

Let's look at a few cases where we can compare fractions without doing too much work. To do this, we will work through a couple of examples and then draw some important conclusions.

Use \(\gt\), \(\lt\), or \(=\) to compare the numbers \( \dfrac{4}{7} \) and \( \dfrac{2}{7} \).

Solution

Consider these fractions as part of a whole chocolate bar. Since the denominators of our fractions are both \(7\), we can divide the whole chocolate bar into \(7\) equal pieces.

Two chocolate bars placed side by side with seven pieces each.

\(\dfrac{4}{7}\) means that you would get \(4\) pieces, while \(\dfrac{2}{7}\) means that you would get \(2\) pieces.

Same chocolate bars. Now, on the right chocolate bar, two pieces have been highlighted.

So say you really like chocolate, which one would you choose? I know I would choose \(4\) pieces, because it gives me more chocolate. 

What this tells us is that \(\dfrac{4}{7}\) of a chocolate bar is greater than \(\dfrac{2}{7}\) of a chocolate bar.

Same chocolate bars, with a greater than symbol comparing the highlighted pieces. Four pieces on the left is greater than the two pieces on the right.

Source: Chocolate - al62/iStock/Thinkstock

We say that \(\dfrac{4}{7}\) is greater than \(\dfrac{2}{7}\).

We write this as:

\(\Large \dfrac{4}{7} > \dfrac{2}{7} \)

In this example, we use the fact that the denominators were both the same to determine which fraction was larger.

This is an important fact that you could use to compare any two fractions with a like denominator.

If two positive fractions with the same denominator are compared, the fraction with the larger numerator is the larger fraction.

Example 4

Let's try one more example to make sure that we understand.

On paper, use \(\gt\), \(\lt\), or \(=\) to compare the numbers \( \dfrac{6}{13} \) and \( \dfrac{9}{13} \).

Take a moment to try this problem on your own.

Solution

We discovered an important fact, during our last example. We determined that if two fractions with the same denominator are compared, the fraction with the largest numerator is the greatest.

If we apply this reasoning to our new example, we first know that since the denominators are the same, they're both \(13\), then we can actually compare the numerators. Since the numerator \(6\) is less than \(9\), we have determined that \(\dfrac{6}{13}\) is less than \(\dfrac{9}{13}\).

\(\dfrac{6}{13} \lt \dfrac{9}{13}\)

If this is still challenging for you to visualize, then draw it out.

Let's go back to our chocolate bar. Since the denominators are both \(13\), we look at our chocolate bar cut into \(13\) pieces.

Chocolate bar with 13 pieces.

Again, you want to ask yourself, if you really like chocolate, do you want \(6\) pieces of this chocolate bar?

Same chocolate bar. Six pieces are highlighted.

Or do you want \(9\) pieces?

Same chocolate bar. This time 9 pieces are highlighted.

Source: Chocolate - al62/iStock/Thinkstock

\(9\) pieces gives you more chocolate. From that, we can conclude that \(\dfrac{6}{13}\) is less than \(\dfrac{9}{13}\).

If at any point you find it challenging to visualize which fraction is larger, always remember that you can draw yourself a picture to help you visualize what's going on.

Try This Problem Revisited

Recall Choice 2 from the "Try This" problem, where you compared \(3\) small squares to \(5\) small squares, that asked us to determine which picture represented a larger total area:

Three small squares on the left and five small squares on the right.

This is the same concept as comparing fractions with like denominators.

In both groups, all pieces are the same size; thus, whichever group has more pieces is larger.

When comparing fractions with like denominators, always ask yourself, if the pieces are the same size, which is larger, \(3\) of them or \(5\) of them. Now that we have done a few examples together, try and work through one on your own.

Check Your Understanding 2

Question (Version 1)

Use \(\lt\) or \(\gt\) to compare the two fractions.

\(\dfrac{21}{25}~\boxed{\phantom \square}~\dfrac{2}{25}\)

Answer (Version 1)

\(\dfrac{21}{25} ~\gt ~\dfrac{2}{25}\)

Feedback (Version 1)

\(\dfrac{21}{25}\) is greater than \(\dfrac{2}{25}\) because both fractions have the same denominator and the numerator \(\dfrac{21}{25}\) is greater than the numerator \(\dfrac{2}{25}\).

Question (Version 2)

Use \(\lt\) or \(\gt\) to compare the two fractions.

\(\dfrac{6}{23}~\boxed{\phantom \square}~\dfrac{7}{23}\)

Answer (Version 2)

\(\dfrac{6}{23} ~\lt ~ \dfrac{7}{23}\)

Feedback (Version 2)

\(\dfrac{6}{23}\) is less than \(\dfrac{7}{23}\) because both fractions have the same denominator and the numerator of \(\dfrac{6}{23}\) is less than the numerator of \(\dfrac{7}{23}\).


Fractions with Like Numerators

Example 5

In addition to being able to easily compare two fractions that have the same denominator, when two fractions have the same numerator, we can also compare those by inspection. Again, we're going to work through a couple of examples to show how we can do this.

Use \(\gt\), \(\lt\), or \(=\) to compare \( \dfrac{3}{8} \) and \( \dfrac{3}{4} \).

Let's first think of these fractions as part of a pizza.

Two pizzas with the fraction 3 over 8 beside the first pizza, and 3 over 4 beside the second pizza.

Remember the denominator of each fraction tells us how many pieces each pizza is cut into. Since the denominators of these two fractions are not the same, the slices of each pizza are actually of a different size.

First pizza is split into 8 parts. Second pizza is split into 4 parts to match the denominators.

We now look to the numerator in each fraction, and we notice that they are the same. 

Same two pizzas, except now the numerators are highlighted.

We are going to take three slices from each pizza.

Both pizzas now display only 3 slices. The 3 over 4 pizza has more area than the 3 over 8 pizza.

Source: Pizza - Zack Middleton/flickr/CC BY SA 2.0 (adapted)

If you're really hungry, which pizza would you take your three slices from? I know I would take three pieces from the second pizza, because they are larger. The slices in the first pizza are smaller, because the whole is divided into more pieces than the second pizza is.

To answer the question, we say \(\dfrac{3}{8}\) is less than \(\dfrac{3}{4}\).

We would write this as:

\(\Large \dfrac{3}{8} \lt \dfrac{3}{4} \)

This leads us to an important fact.

If two positive fractions with the same numerator are compared, the one with the smaller denominator is the larger fraction.

It may seem strange at first that a smaller denominator means a larger fraction. However, think back to our example with the pizzas. When the denominator was smaller, the size of each slice in the pizza was larger. Larger slices means more pizza.

Example 6

Let's look at one more example together before you try one on your own.

Use \(\gt\), \(\lt\), or \(=\) to compare \( \dfrac{7}{13} \) and \( \dfrac{7}{9} \).

Let's try to use the important fact from our previous example. Remember, it said that if two fractions with the same numerator are compared, the one with the smaller denominator is the larger fraction.

Applying this reasoning to our new example, we note first that our fractions do have the same numerator, which is \(7\). So we look to their denominators: \(13\) is larger than \(9\).

Therefore, we can conclude that \(\dfrac{7}{13}\) is smaller than \(\dfrac{7}{9}\).

\(\dfrac{7}{13} \lt \dfrac{7}{9}\)

If this is still challenging for you to visualize, draw it out. Let's go back to our example using pizzas.

Two pizzas with the fraction 7 over 13 beside the first pizza, and 7 over 9 beside the second pizza.

When we look at \(\dfrac{7}{13}\) and \(\dfrac{7}{9}\) drawn out using pizzas, then we can see that the slices in the second pizza are larger than the slices in the first.

First pizza is split into 13 parts. Second pizza is split into 9 parts.

This means that if we chose \(7\) slices from each pizza, the second one would yield us more overall pizza in the end.

First and second pizza showing 7 slices.

We can conclude from our diagrams that \(\dfrac{7}{13}\) is less than \(\dfrac{7}{9}\).

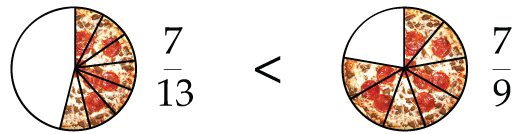
There is more pizza showing in the 7 over 9 case than in the 7 over 13 case.

Source: Pizza - Zack Middleton/flickr/CC BY SA 2.0 (adapted)

Recall the Try This problem we did at the beginning of this lesson. Remember when I asked you to compare three small squares with three large squares and to determine which had a greater area? 

Three small squares compared to three large squares.

This concept is actually the exact same as comparing fractions with like numerators. In both cases, the size of each piece is different, but you're taking the same amount.

Check Your Understanding 3

Question

Use \(\gt\), \(\lt\), or \(=\) to compare \( \dfrac{15}{16} \) and \( \dfrac{15}{8} \).

\(\dfrac{15}{16}~\boxed{\phantom \square}~\dfrac{15}{8}\)

Answer 

\(\dfrac{15}{16} \lt \dfrac{15}{8}\)

Feedback 

Since \( \dfrac{15}{16} \) and \( \dfrac{15}{8} \) have a common numerator of \(15\), the fraction with the larger denominator is the smaller fraction. Since \(16\) is greater than \(8\), the fraction \( \dfrac{15}{16} \) is less than \( \dfrac{15}{8} \). 

Example 7

Let's put everything that we have learned in this lesson together in one final example.

Three students are competing in a race. After \( 10 \) minutes, Anne has finished \( \dfrac{3}{8} \) of the race, Blair has completed \( \dfrac{3}{7} \) of the race, and Cooper is \( \dfrac{5}{7} \) of the way through the race.

If all students maintain their current standing, who will come in first, second, and third place?

Take a moment to try this problem on your own.

Solution

To solve this problem, we need to first choose two fractions to compare.

We notice that 3/7 and 5/7 have a common denominator, so it makes sense that we can start there.

\(\dfrac{3}{7} \lt \dfrac{5}{7}\)

Since the numerator \(3\) is less than the numerator \(5\), we can conclude that \(\dfrac{3}{7}\) is less than \(\dfrac{5}{7}\).

If we think about what this would look like on a number line, \(\dfrac{3}{7}\) would be to the left of \(\dfrac{5}{7}\).

Next, we notice that \(\dfrac{3}{8}\) and \(\dfrac{3}{7}\) have a common numerator, so we can compare those two fractions next.

\(\dfrac{3}{8} \lt \dfrac{3}{7}\)

Since the denominator of \(\dfrac{3}{8}\) is greater than the denominator of \(\dfrac{3}{7}\), we conclude that \(\dfrac{3}{8}\) is less than \(\dfrac{3}{7}\).

Thinking about this on the number line, Since \(\dfrac{3}{8}\) is less than \(\dfrac{3}{7}\), this means that \(\dfrac{3}{8}\) would be to the left of \(\dfrac{3}{7}\) on the number line.

In this example, I've used the number line as a tool to keep track of how my numbers compare to each other. To summarize our results, I can read the numbers on the number line, starting from left and moving to the right.

When we combine our work, we get

\( \class{timed add16-hl2 remove13-hl2}{\dfrac{3}{8}} \lt \dfrac{3}{7} \class{timed in18}{\lt \class{timed add16-hl2 remove13-hl2}{\dfrac{5}{7}}} \)

It's interesting, because while answering this question, we've actually managed to show something else. We have shown that \(\dfrac{3}{8}\) is less than \(\dfrac{5}{7}\). Think about how the fraction \(\dfrac{3}{7}\) actually helped you to compare the fractions that don't have a common numerator or a common denominator.

Our final step is to go back and answer our question. So since \(\dfrac{3}{8}\) is less than \(\dfrac{3}{7}\), which is less than \(\dfrac{5}{7}\), we conclude that Cooper will finish first, Blair will finish second, and Anne will finish third.

Check Your Understanding 4

Question

Order the fractions, \(\dfrac{1}{5}\), \(\dfrac{3}{4}\), and \(\dfrac{3}{5}\) from least to greatest. 

\(\boxed{\phantom\square} \lt \boxed{\phantom\square} \lt \boxed{\phantom\square}\)

Answer 

\(\dfrac{1}{5} \lt \dfrac{3}{5} \lt \dfrac{3}{4}\)

Feedback 

Notice that \(\dfrac{3}{5}\) and \(\dfrac{1}{5}\) have like denominators while \(\dfrac{3}{4}\) and \(\dfrac{3}{5}\) have like numerators. 

\(\dfrac{1}{5}\) is smaller than \(\dfrac{3}{5}\) and \(\dfrac{3}{4}\). Comparing \(\dfrac{3}{4}\) and \(\dfrac{3}{5}\) using the fact that these fractions have like numerators tells us that \(\dfrac{3}{5}\) is smaller than \(\dfrac{3}{4}\).

Take It With You

In the pre-season games, Jason completed \(\dfrac{2}{3}\) of his passes and Jan completed \(\dfrac{5}{6}\) of his passes.

Which player would you start in the opening game?

Provide a reason for your choice.