Hot Air Balloon Summary
Introduction
When adding and subtracting integers, we can identify patterns that allow us to group similar problems. So far, we've seen four general scenarios:
- Add a positive integer to an integer.\[(-2)+9\]
- Add a negative integer to an integer.\[(-2)+(-3)\]
- Subtract a positive integer from an integer.\[(-2)-1\]
- Subtract a negative integer from an integer.\[(-2)-(-4)\]
Let's now take some time to describe each scenario, using the analogy of a hot air balloon.
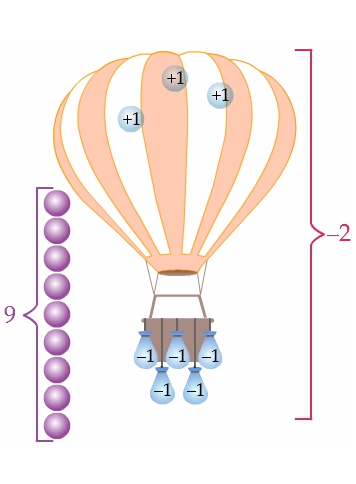
If we look at our hot air balloon, it has both units of air and sandbags. Each unit of air represents \(+1\). So in this case, we have \(3\) units of air, which represent the integer, \(+3\). Each sandbag represents \(-1\). So in this case, we have \(5\) sandbags which represent the integer, \(-5\).
Overall, our hot air balloon represents \(-2\), because that is the total of \(+3\) and \(-5\). What this means is that we have \(2\) more sandbags than units of air.

Source: Hot Air Balloon - University of Waterloo
1. Adding a Positive Integer
We're now going to use our hot air balloon to help us answer some math problems. Consider what would happen when we add a positive integer to any number.
Consider the problem
\(\class{hl2}{(-2)}+\class{hl3}9\)
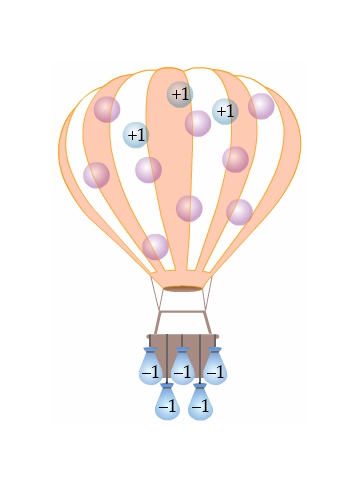
Using our hot air balloon, we remember that it already represents \(-2\). To add \(9\) to \(-2\), means that we add \(9\) units of air to the balloon.
So ask yourself, what would happen to the balloon with this addition of air?
We add nine more air particles to the balloon, causing it to rise.
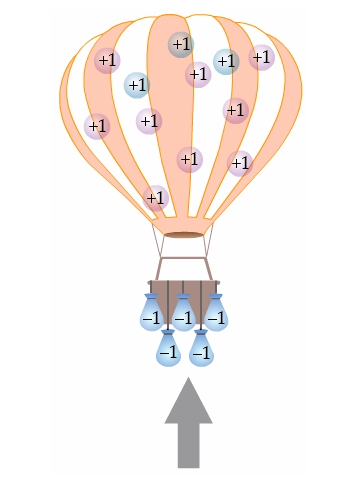
Source: Hot Air Balloon - University of Waterloo
But what does this mean mathematically? Well, when we add a positive integer to a number, it's just like adding air to the balloon.
Adding a positive integer to any number will result in an increase.
I encourage you to try a few more examples on your own to convince yourself that this is true.
2. Adding a Negative Integer
With our previous example in mind, how can we think about adding a negative?
Consider the problem
\(\class{hl2}{(-2)}+\class{hl3}{(-3)}\)
Again, our hot air balloon represents \(-2\). So if we want to add \((-3)\), it means that we need to add \(3\) sand bags. What's going to happen when we do this?
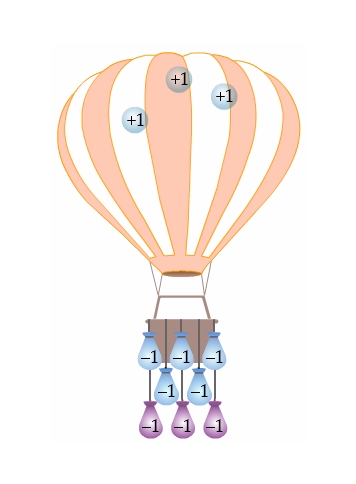
We add three more sand bags to the balloon, causing it to fall. Adding sandbags is going to cause the balloon to fall towards the ground, because sandbags weigh the balloon down.

Source: Hot Air Balloon - University of Waterloo
At this point, you should be asking yourself, what does this tell us mathematically.
Adding a negative integer is always like adding sandbags, which leads to this important fact.
Adding a negative integer to any number will result in a decrease.
Come up with a few examples on your own right now to convince yourself that this is true.
3. Subtracting a Positive Integer
Let's now look at how subtraction works.
Consider the problem
\(\class{hl2}{(-2)}-\class{hl3}1\)
To subtract \(1\) from \((-2)\), we must remove \(1\) unit of air from the balloon, because each unit of air represents \(+1\).
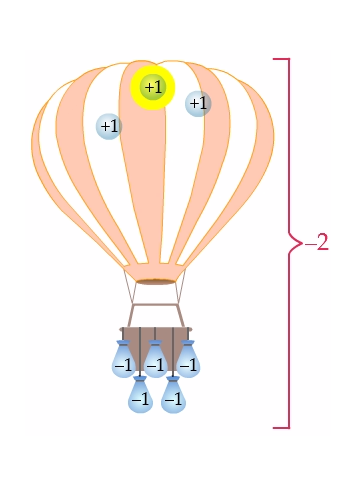
When we do this, will the hot air balloon rise or fall?

We remove \(1\) air particle from the balloon, causing it to fall. Convince yourself that removing units of air is going to cause the balloon to fall towards the ground.
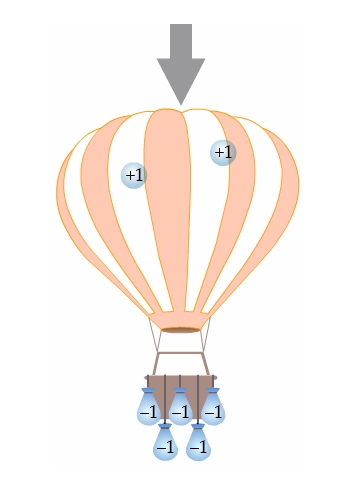
Source: Hot Air Balloon - University of Waterloo
Mathematically this means that subtracting a positive integer is just like removing air from the balloon.
Subtracting a positive integer from any number will result in a decrease.
Again, as an exercise, try some more examples on your own.
4. Subtracting a Negative Integer
Finally, we need to consider the last case, which means we need to consider how to subtract a negative.
Let's look at the question,
\(\class{hl2}{(-2)}-\class{hl3}{(-4)}\)
In our hot air balloon analogy, subtracting \((-4)\) means to remove \(4\) sandbags from the basket of the hot air balloon.
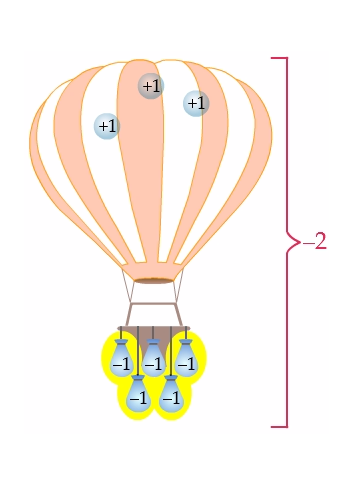
When we remove \(4\) sandbags, the hot air balloon will rise, because there are less sandbags weighing it down.
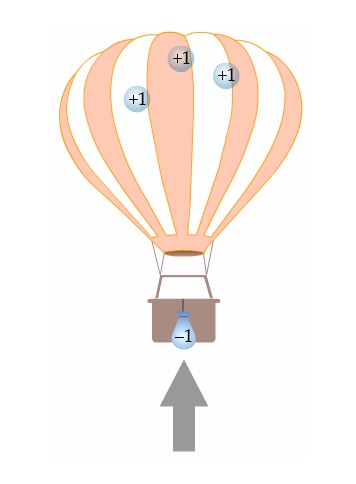
Source: Hot Air Balloon - University of Waterloo
Mathematically, this tells us that subtracting a negative integer is just like removing sandbags from the balloon.
Subtracting a negative integer from any number results in an increase.
This is a hard idea to visualize. I really encourage you to try a few more examples of this case on your own, before you move on to the next part of the lesson.
Summary
Let's look at all four examples together. We have two addition problems, \(\class{hl2}{(-2)} + \class{hl3}{9}\) and \(\class{hl2}{(-2)} + \class{hl3}{(-3)}\), and two subtraction problems, \(\class{hl2}{(-2)} - \class{hl3}{1}\) and \(\class{hl2}{(-2)} - \class{hl3}{(-4)}\). And at first, we would want to say that the addition problems are similar and the subtraction problems are similar, but now that we've illustrated each of these problems using a hot air balloon, you should have noticed something else.
\(\class{hl2}{(-2)}+\class{hl3}{9}\)

\(\class{hl2}{(-2)}+\class{hl3}{(-3)} \)

\(\class{hl2}{(-2)} -\class{hl3}{1} \)

\(\class{hl2}{(-2)}- \class{hl3}{ (-4)} \)

We notice that two of these problems caused the balloon to rise. And two of these problems caused the balloon to fall.
\(\class{hl2}{(-2)}+\class{hl3}{9}\)

\(\class{hl2}{(-2)}+\class{hl3}{(-3)} \)

\(\class{hl2}{(-2)} -\class{hl3}{1} \)

\(\class{hl2}{(-2)}- \class{hl3}{ (-4)} \)

Source: Hot Air Balloon - University of Waterloo
Let's start by looking at those two expressions that caused our balloon to rise.
The first thing you should notice is that \(\class{hl2}{(-2)} + \class{hl3}{9}\) is an addition problem, but \(\class{hl2}{(-2)} - \class{hl3}{(-4)}\) is a subtraction problem. So what's actually going on here?
Well, adding air naturally will cause the balloon to rise, but subtracting what's weighing it down has that exact same effect. Adding a positive integer or subtracting a negative integer both cause an increase.
Let's now look to the other two expressions, \(\class{hl2}{(-2)} + \class{hl3}{(-3)}\) and \(\class{hl2}{(-2)} - \class{hl3}{1}\), both of which caused our balloon to fall.
We saw that removing air will cause the balloon to fall, but adding sandbags has the exact same effect. Subtracting a positive integer and adding a negative integer both result in a decrease.
Once we start to perform operations with integers, we can really begin to see more connections between addition and subtraction. Use these connections to help you with your mental arithmetic.
Check Your Understanding 6
Question
Solve as many problems as you can in one minute
- \((-9)-21\)
- \((-14) - (-31)\)
- \(10+31\)
- \((-10)+(-5)\)
- \(1+6\)
- \(19+15\)
- \((-17)+(-15)\)
- \(3+4\)
- \((-15)-5\)
- \(8-(-36)\)
- \(2-25\)
Answer
- \((-9)-21=(-30)\)
- \((-14) - (-31)=17\)
- \(10+31=41\)
- \((-10)+(-5)=(-15)\)
- \(1+6=7\)
- \(19+15=34\)
- \((-17)+(-15)=(-32)\)
- \(3+4=7\)
- \((-15)-5=(-20)\)
- \(8-(-36)=44\)
- \(2-25=(-23)\)
Take It With You
Subtraction is not commutative.
For example,
\(37 - 19 \neq 19 - 37\)
Explain why
\(37-19+3\) and \((-19)+37+3\)
are equal.
How might this help you when performing mental arithmetic?