Alternative Format

Try This

Points of Reference

Consider the following city map and assume that Geet lives in a house near point \(G\).

Source: City Map - DROSOSTALITSA/iStock/Getty Images

We could describe many locations around town using Geet's house as a point of reference. For example, Geet can reach the market labeled \(M\) by traveling \(2\) blocks west and then \(1\) block north. He could reach the library, labeled \(L\), by traveling \(2\) blocks east and then \(2\) blocks south. Now, if Geet's friend Wendy lives across town in a house near point \(W\), then how we would describe the location of the market and the library from Wendy's house would be different because the point of reference has changed.

Lesson Goals

• Construct the Cartesian coordinate system.
• Plot points and state the coordinates of points on the Cartesian plane.
• Construct shapes on the Cartesian plane.

Try This!

The following triangle has an area of \(30\) square units.

For reference, we overlay a pair of perpendicular lines and say that one of the vertices is located at \((0, 0)\).

How might you describe the location of the other \(2\) vertices of this triangle? 

Think about this problem, then move on to the next part of the lesson.

Introducing the Cartesian Plane

Review of Ordered Pairs

Consider the points labeled \(O\) and \(B\) on the following grid. We know that the point \(B\) is above the point \(O\) and to the right of \(O\), but what numerical value might we assign to the point \(B\)? In math, we need a way to describe the position of points on a grid.

Recall that you have previously seen how to construct a coordinate grid by drawing a horizontal axis and a vertical axis that intersect at the origin.

We use an ordered pair to describe the coordinates of a point. The origin is our point of reference, and so we give it the coordinate, \((0, 0)\).

The coordinates of point \(B\) are \((6, 4)\), because \(B\) is located \(6\) units to the right and \(4\) units up from the origin.

Remember that in an ordered pair, the first number tells you the horizontal distance from the origin, and the second number tells you the vertical distance from the origin.

Ordered pair: \((6,4)\)

•  \(6\) is the horizontal distance from the origin, and
• \(4\) is the vertical distance from the origin.

Check Your Understanding 1

Question

Plot the points \((5,7)\) and \((7,7)\) on the grid below.

Answer

Created with GeoGebra. Author: University of Waterloo. CC BY-NC-SA 4.0. https://ggbm.at/KN4h94d3

Feedback

The ordered pair \((5,7)\) is located \(5\) units to the right and \(7\) units up from the origin.

The ordered pair \((7,7)\) is located \(7\) units to the right and \(7\) units up from the origin.

Online Version

https://ggbm.at/KN4h94d3

The Cartesian Plane

In real world applications, our point of reference could move around. For example, consider the following map. What if the point of reference is where you live, which is located somewhere in the middle?

We now need a way to reference locations all around your home. Lets start by considering a number line. And we're going to draw the number line so that \(0\) is where you live. Notice that we can now use negative numbers to describe locations that are to the left of your home, and positive numbers that describe locations that are to the right of your home.

Similarly, we can draw a vertical number line, just like we did when representing temperature. On this number line, up means positive and down means negative.

The grid we saw before has been extended to include negative integers. As a result, it is now called the Cartesian coordinate system, which describes the positions of points and lines in a plane.

Notice that the horizontal and vertical axes are essentially two number lines, which we now call the \(x\)-axis and the \(y\)-axis, respectively. Together, they are called the coordinate axes.

The two lines intersect at a right angle at the point known as the origin, usually labeled \(0\).

Notice that the axes now divide the plane into four parts known as the first, second, third, and fourth quadrants, which we label using Roman numerals for I, II, III, and IV. The plane that is formed is called the Cartesian plane, or the coordinate plane.

Cartesian coordinate system: Describes the positions of points and lines in a plane.

Source: City - Michellsola/iStock/Thinkstock

Check Your Understanding 2

Question

Label the Cartesian plane with the following terms:

• Quadrant I
• Quadrant II
• Quadrant III
• Quadrant IV
• Origin
• \(x\)-axis
• \(y\)-axis

Answer

Created with GeoGebra. Author: University of Waterloo. CC BY-NC-SA 4.0. https://ggbm.at/zSkKJ6j6

Online Version

https://ggbm.at/zSkKJ6j6

Plotting Ordered Pairs

Ordered Pairs on the Cartesian Plane

Consider the following Cartesian coordinate system. The position of the point \(A\) can be described by the ordered pair \((-3, 1)\). The position of the point \(B\) can be described by the ordered pair \((2, 3)\). Knowing this, how might we describe the position of the point \(C\)?

Notice that the point \(C\) corresponds to the value \(-1\frac{1}{2}\) on the \(x\)-axis and the value \(3\frac{1}{2}\) on the \(y\)-axis.

Therefore, we would describe the point \(C\) using the ordered pair, \((-1\frac{1}{2}, 3\frac{1}{2})\).

In fact, the position of any point, let's call it \(P\) on the plane, can be described by an ordered pair \((a, b)\) of numbers. We obtain the value of a from where the vertical line through \(P\) intersects the \(x\)-axis. Similarly, we obtain the value of \(b\) from where the horizontal line through \(P\) intersects the \(y\)-axis. We call \(a\) the \(x\)-coordinate and we call \(b\) the \(y\)-coordinate of the point \(P\).

The point \(P\)

• has coordinates \((a,b)\), and
• is referred to as \(P(a,b)\).

We can locate the point \(P\) in the plane if we know its \(x\)- and \(y\)-coordinates.

Example 1

Solution

Let's start with point \(A\). We draw a vertical line from the point \(A\) to the \(x\)-axis, and note that the point that corresponds to the value \(-3\) on the \(x\)-axis.

Similarly, we draw a horizontal line from the point \(A\) to the \(y\)-axis, and note that the point that corresponds to the value \(-4\) on the \(y\)-axis.

Therefore, the coordinates of point \(A\) are \((-3, -4)\).

We can follow the same strategy for point \(B\). Drawing the vertical line, we see that point \(B\) corresponds to the value \(4\frac{1}{2}\) on the \(x\)-axis.

And drawing the horizontal line, we see that it corresponds to the value \(-2\) on the \(y\)-axis.

Therefore, the coordinates of point \(B\) are \((4\frac{1}{2}, -2)\).

Following the same strategy for point \(C\), we see that it corresponds to the value of \(-4\) on the \(x\)-axis and the value \(2\frac{1}{2}\) on the \(y\)-axis.

Therefore, the coordinates of point \(C\) are \((-4, 2\frac{1}{2})\).

 

Check Your Understanding 3

Question

What are the coordinates of points \(A\) and \(B\)?

Feedback

Use the vertical and horizontal lines from each point to the \(x\)- and \(y\)-axes to help you.

Created with GeoGebra. Author: University of Waterloo. CC BY-NC-SA 4.0. https://ggbm.at/DQWZnZWW

Answer

The points are \(A(-2,-4)\) and \(B(4,-5)\).

Online Version

https://ggbm.at/DQWZnZWW

Ordered Pairs in the Same Quadrant

Consider the points \(A(2,5)\), \(B(1,7)\), and \(C(6,2)\), which are all located in the first quadrant.

Both the \(x\)- and \(y\)-coordinates of all three points are positive.

This is true of all points in the first quadrant. 

Explore This 1

Description

Explore the relationship between each quadrant and the sign of the \(x\)- and \(y\)- coordinates for all points in the quadrant.

Created with GeoGebra. Author: University of Waterloo. CC BY-NC-SA 4.0. https://ggbm.at/SdgedJwx

Notice that

• all points in Quadrant I have positive \(x\)-coordinates and positive \(y\)-coordinates \((+,+)\),
• all points in Quadrant II have negative \(x\)-coordinates and positive \(y\)-coordinates, \((-,+)\),
• all points in Quadrant III have negative \(x\)-coordinates and negative \(y\)-coordinates, \((-,-)\), and
• all points in Quadrant IV have positive \(x\)-coordinates and negative \(y\)-coordinates, \((+,-)\).

Online Version

https://ggbm.at/SdgedJwx

Summary of Explore This

In your explorations, you should have noticed some similarities between points in the same quadrant. We will summarize these findings in the diagram below.

As we saw before, if a point is in the first quadrant, then its \(x\) and \(y\)-coordinates are both positive.

If a point is in the second quadrant, its \(x\)-coordinate is negative, and its \(y\)-coordinate is positive.

If a point is in the third quadrant, then its \(x\) and \(y\)-coordinates are both negative.

If a point is in the fourth quadrant, its \(x\)-coordinate is positive, and its \(y\)-coordinate is negative.

But what if a point is on an axis instead of inside one of the quadrants? We can still make a general observation depending on which axis the point is on. If a point is on the \(x\)-axis, then its \(y\)-coordinate is \(0\).

If a point is on the \(y\)-axis, then its \(x\)-coordinate is \(0\).

Knowing this information can help us to locate and plot points more efficiently on the Cartesian plane.

Check Your Understanding 4

Question

Plot the point \((3,-4)\) on the grid below.

Feedback

Since the \(x\)-coordinate is positive and the \(y\)-coordinate is negative, we can plot the point in Quadrant IV. 

This point corresponds to a value of \(3\) on the \(x\)-axis and \(-4\) on the \(y\)-axis.

Answer

The \(x\)-coordinate is positive and the \(y\)-coordinate is negative, so the point is in Quadrant IV.

Created with GeoGebra. Author: University of Waterloo. CC BY-NC-SA 4.0. https://ggbm.at/myBeNYgZ

Online Version

https://ggbm.at/myBeNYgZ

Horizontal and Vertical Distances

Horizontal Distance

We can find the horizontal distance between any two points by counting the number of units between them.

For example, on the following Cartesian plane, the horizontal distance between each pair of points is \(4\) units.

Explore This 2

Description

Explore the horizontal distance between two points.

Consider the points \((-3,4)\) and \((4,4)\).

Using the Grid

Created with GeoGebra. Author: University of Waterloo. CC BY-NC-SA 4.0. https://ggbm.at/CepwkKU4

There is a distance of \(7\) units between the points.

Using Coordinates

Subtract the \(x\)-coordinates of each point.

\(4 - (-3) = 7\)

Online Version

https://ggbm.at/CepwkKU4

Example 2

Solution

The horizontal distance between two points is equal to the positive difference between their
\(x\)-coordinates.

The difference between the \(x\)-coordinates can be calculated in two possible ways:

Or, we have the following.

The sign of the result tells us the direction we travel to get from one value to the other. But regardless, the difference between \(-8\) and \(3\) is \(11\) units.

Therefore, the horizontal distance between the points \((-8,6)\) and \((3,6)\) is \(11\) units. 

 

Vertical Distance

The vertical distance between two points is equal to the positive difference between their
\(y\)-coordinate values.

Solution

The \(y\)-coordinates of the points are \(7\) and \(-1\). We know that we can subtract the values in either order, but subtracting smaller value from the larger value will result in the positive difference. 

\[7 - (-1) = 8\]

Therefore, the vertical distance between the points \((-4,7)\) and \((-4,-1)\) is \(8\) units.

Check Your Understanding 5

Description

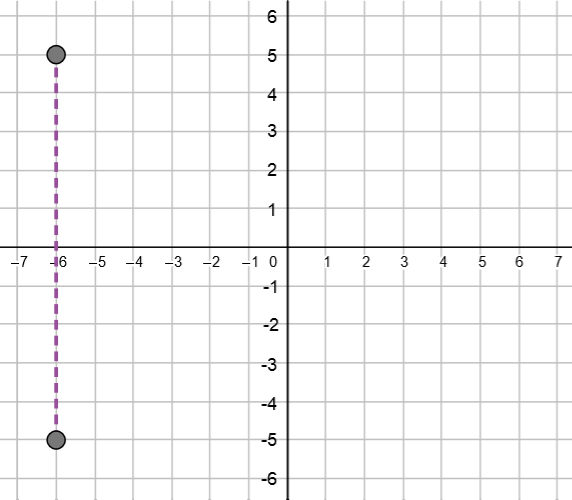
Find the vertical distance between the points \((-6,-5)\) and \((-6,5)\).

Feedback

To find the vertical distance between the two points, subtract their \(y\)-coordinates.

Answer

To find the vertical distance between the two points, we can subtract their \(y\)-coordinates.

\(5 - (-5) =10\)

Thus, the vertical distance between the points is \(10\) units.

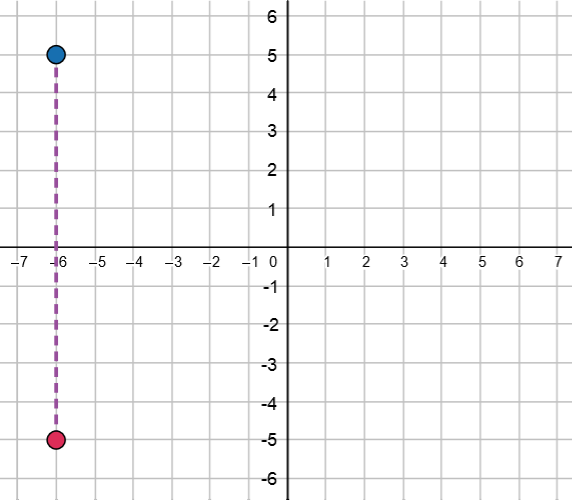
Created with GeoGebra. Author: University of Waterloo. CC BY-NC-SA 4.0. https://ggbm.at/Vt4XmfnY

Online Version

https://ggbm.at/Vt4XmfnY

Try This Problem Revisited

Solution

We can start by doing some rough work to figure out the dimensions of the triangle that we are looking to draw before we work on the Cartesian plane.

If a triangle has an area of \(30\) square units, then

\[\begin{align*} \dfrac{b \times h}{2} &=30 \\ \class{timed in5}{b \times h} &\; \class{timed in5}{= 60} \end{align*}\]

Some possibilities include the following:

• \(b=10\) and \(h=6\)
• \(b=5\) and \(h=12\)
• \(b=4\) and \(h=15\)

As an example I will find the coordinates of the triangle where the height is \(6\) units and the base is \(10\) units.

For ease I'm going to label the two unknown points \(A\) and \(B\).

We have that the point \(A\) is \(6\) units below the point with coordinates \((0, 0)\), or the origin. The coordinates of this point are \((0, -6)\).

Next, we have that the point \(B\) is \(10\) units to the right of point \(A\). The coordinates of this point are \((10, -6)\).

Therefore, \(A\) at \((0, -6)\) and \(B\) at \((10, -6)\) could describe the location of the other two vertices.

As an exercise try finding the coordinates of the triangle if the height and the base are different than the \(6\) units and \(10\) units, respectively.

Check Your Understanding 6

Question

A right triangle has an area of \(4\). If one of its vertices has the coordiantes \((-1,6)\), and another vertex has the coordinates \((1,6)\), write possible coordinates for the third vertex.

Answers

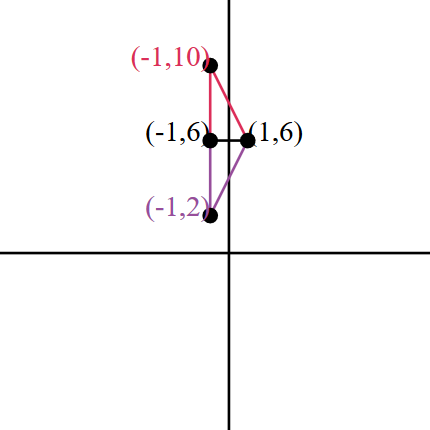
• \((-1,10)\)
• \((1,10)\)
• \((-1,2)\)
• \((1,2)\)

Feedback

The distance between the points \((-1,6)\) and \((1,6)\) is \(2\) units.

We will consider this side to be the base of the triangle. That mean

\[\begin{align*} 4 & = \dfrac{2\times h}{2} \\ 8 & = 2 \times h\end{align*}\]

Thus, \(h=4\).

There are four possibilities that would give a triangle with a height of \(4\) units.

This gird shows the point \((-1,10)\) and the point \((-1,2)\).

This grid show the point \((1,10)\) and the point \((1,2)\).

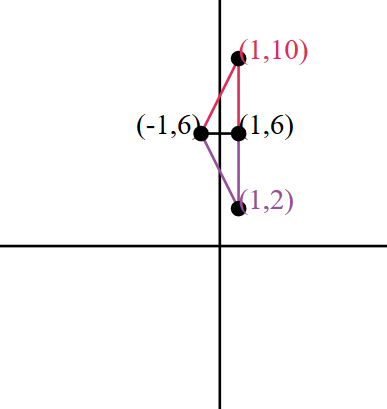
Take It With You

The diagonals of a rectangle intersect at \((0,0)\).

The dimensions of this rectangle are \(10\) units and \(6\) units.

What are the possible coordinates of the four corners of the rectangle?