Alternative Format

Try This

Graph Review

Some mathematicians love looking over tables of numbers. However, sometimes it is helpful to present that information in a more visual way.

A graph is a visual representation of information. It can be a powerful tool in communicating data in a clear and concise way. You have likely organized data into different types of graphs before.

For instance, a pictograph uses pictures or symbols to represent frequencies for categorical data.

Number of Watermelons Sold

Day \(1\): 

Day \(2\): 

Day \(3\): 

Source: Watermelon - paggiest/iStock/Getty Images Plus

A stem and leaf plot represents numerical discrete data by displaying numbers based on their digits.

Popsicle Stick Tower Height

Stem	Leaf
\(0\)	\(9\)
\(1\)	\(2\), \(2\), \(3\), \(7\), \(7\), \(8\)
\(2\)	\(0\), \(4\), \(5\), \(5\), \(9\)
\(3\)	\(0\), \(0\), \(1\), \(1\)

A bar graph has vertical or horizontal bars that represent the frequency of data.

A line graph represents data points with line segments and often represents data that occurs over a time span.

There are many more types of graphs, including circle graphs, which we will spend some time discussing in this lesson. With so many graphs, how do we know which graph to use to best represent a data set?

Lesson Goals

• Identify key features of circle graphs.
• Draw circle graphs.
• Choose the most appropriate graph to display a data set.

Try This!

\(200\) people were asked to name an animal that swims.

The following circle graph displays their answers with the number of responses in brackets and the corresponding percent.

Source: Animals - Nadzeya_Dzivakova/iStock/Getty Images

1. How many people responded with “Dolphin?”
2. What percent of the total responses does the response “Dolphin” represent?

Think about this problem, then move on to the next part of the lesson.

Reading Circle Graphs

Try This Problem Revisited

Let's take up or Try This Problem right away.

Source: Animals - Nadzeya_Dzivakova/iStock/Getty Images

Solution

A circle graph is a special type of graph that represents a whole set of data that is subdivided into categories. 

1. In this survey, the whole data set is the \(200\) responses from the survey participants. The total number of responses in the circle graph should add to \(200\).
   Let's add the numbers that we currently have.
   \[80+40+20+10 =150\]
   The number of dolphin responses must be \(200-150 =50\).
   Therefore, the number of dolphin responses was \(50\).
2. Next, we want to determine what percent of the total responses that represents. Since a circle graph represents all of the responses, the total percents in the graph should add to \(100\%\). Therefore, if we total all of the percents in the graph, they should add to \(100\%\).
   Let's add the percents that we currently have.
   \[40\%+20\%+10\%+5\% =75\%\]
   The percent of people that responded dolphin must be \(100\%-75\% = 25\%\).
   Therefore, the percent of people that responded dolphin is \(25\%\).

Reading a Circle Graph

A circle graph is an appropriate way to represent categorical data.

Here is a circle graph of the different car types on a used car lot.

Source: Cars - MuchMania/iStock/Getty Image

The whole data set in this case is all of the cars for sale on the used car lot. Since the data describes different types of cars, it is categorical data. 

From this graph, we can quickly notice some relationships between the different categories. 

Observations

• Notice that sports cars is the smallest piece of the circle. Therefore, sports cars represent the fewest number of cars on the lot.
• There are fewer pick-up trucks than minivans, since the piece of the circle representing pickup trucks is smaller than the piece representing minivans.
• A more challenging question is which car type represents the largest number of cars on the lot. The categories of sedans and minivans are very close in size.

One of the limitations of circle graphs is that it can sometimes be challenging to compare categories on the graph. Especially if the categories are close in size and are not labeled with numerical quantities. 

Adding quantities to the categories in the circle graph allows for better comparisons.

• With the quantities provided it is easier to compare the categories and notice that sedans represent the largest number of cars on the lot since \(31\%\) is greater than \(29\%\).

Notice that the data is described using percent, which suggests it is the relative frequency of each car type. However, the frequency would have also allowed us to compare the categories.

Too Many Categories on a Circle Graph

Here is a circle graph of the genres of books in a school library.

Library Book Genres

There are so many different categories in this circle graph that it is challenging to tell the categories apart, let alone compare them. Sometimes, in a case where there are too many categories, a circle graph of all of the data may not be the best way to display the information.

It might be appropriate to group some of the smallest categories into an “Other” category.

By replacing the smallest categories into an “Other” category: 

• we lose some information in the graph,
• we place focus on the categories that make up the larger share of the total, and
• the graph is visually less cluttered.

Grouping Categories on a Circle Graph

Here's another option that we can use to improve a circle graph with too many categories. We can look at the data and see if there's another way to organize it.

Library Book Genres

In these books genres I noticed that there are both fiction and non-fiction genres in the circle graph. Maybe we should create two circle graphs. One just for fiction genres, and the other just for non-fiction genres.

These graphs are easier to read since there are fewer categories in each graph.

When making circle graphs, we must make decisions about how best to display the data for our intended purpose.

Check Your Understanding 1

Question

The circle graph below shows the results of a recent poll.

Created with GeoGebra. Author: University of Waterloo. CC BY-NC-SA 4.0. https://ggbm.at/W2RKDwQe

What percent of the total responses does sneakers represent?

Answer

\(30\%\) of the total responses represents sneakers.

Feedback

Remember that the percents in the graph must all add to \(100\%\).

Notice that \(37\%+20\%+13\%=70\%\). 

Since the percents in the graph must all add to \(100\%\), the missing percent is \(100\%-70\%=30\%\).

Therefore, \(30\%\) of the total responses represent sneakers. 

Online Version

https://ggbm.at/W2RKDwQe

Creating Circle Graphs

Drawing a Circle Graph

Santo surveyed \(20\) of his neighbours to determine what type of water they drink at home. The following table shows his survey results.

Type of Water	Number of Houses
Tap Water	\(13\)
Filtered Water	\(5\)
Bottled Water	\(2\)

Since type of water is categorical data, Santo decided to create a circle graph to represent the data.

He drew a circle, and divided it into \(20\) even slices, so that each slice would represent \(1\) of the \(20\) houses that were surveyed.

To determine the portion of the circle that represents the tap water users, Santo started at the top of the circle, and counted out \(13\) slices, to represent the \(13\) houses that use tap water.

He labeled this section Tap Water.

To mark off the portion of the circle that represents the filtered water users, Santo started from the edge of the tap water, and counted \(5\) slices to represent the \(5\) houses that used filtered water.

He labeled this section Filtered Water.

This left the \(2\) slices that represent the \(2\) houses that use bottled water. 

Santo labeled this section Bottled Water.

Notice that all of the \(20\) slices of the circle have been used, which indicates that we have included all of the \(20\) houses that were surveyed.

Santo can finish up his circle graph by adding a title, "Drinking Water Type By House."

Drinking Water Type By House

If he chooses, he could add frequency or relative frequency data to each category.

Notice that Santo started with the Tap Water group, which was the largest group. When creating circle graphs, I often start at the top of the circle, with the largest category. And then order the categories from largest to smallest, as I work around the circle in a clockwise direction.

Not all circle graphs are created in this manner. But this method will ensure that categories that are similar in size will be close together, and make for easier comparisons.

Check Your Understanding 2

Question — Part A

The choices of \(25\) campers at a summper camp are shown in the table below. 

Lunch Choice	Number of Students
Sandwich	\(3\)
Pizza	\(21\)
Hot Dog	\(1\)

Divide the following circle graph into the appropriate number of slices.

Created with GeoGebra. Author: University of Waterloo. CC BY-NC-SA 4.0. https://ggbm.at/x8XKP54m

Answer — Part A

The circle graph is divided into \(25\) slices. 

Feedback — Part A

Remember that the number of slices should be equal to the total number of campers.

Question — Part B

The choices of \(25\) campers at a summper camp are shown in the table below. 

Lunch Choice	Number of Students
Sandwich	\(3\)
Pizza	\(21\)
Hot Dog	\(1\)

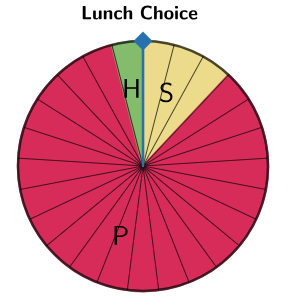
Using the circle graph with the appropriate number of slices from part a), display the data from the table in a circle graph.

Created with GeoGebra. Author: University of Waterloo. CC BY-NC-SA 4.0. https://ggbm.at/x8XKP54m

Answer — Part B

The response Sandwich takes up \(3\) slices, Pizza takes up \(21\) slices, and Hot Dog takes up \(1\) slice.

Feedback — Part B

Remember that all the slices in the graph must be used and that the number of sections for each category in the graph should match the corresponding number in the table.

Online Version

https://ggbm.at/x8XKP54m

360 Degrees in a Circle

I'm not very excited to divide a circle into \(120\) even pieces. That would take quite a long time and would be challenging to do accurately. Thankfully, we can use another strategy using our knowledge of circles.

When you turn all of the way around once, you have completed a \(360^\circ\) turn.

We can confirm this by using our knowledge that a quarter turn is \(90^\circ\).

To turn all of the way around, we can do four quarter turns, or four \(90^\circ\) turns to return back to our starting point.

This means we will have turned \(4\) times \(90^\circ\), for a total of \(360^\circ\).

You may have also heard of a full turn being referred to as a 360 in sports such as skateboarding, snowboarding, BMX freestyle, and other trick sports.

If a full circle represents \(360^\circ\) and a survey had \(120\) participants, how many degrees of the circle will each participant's response represent? 

\(360 \div 120 = 3\)

Therefore, with \(120\) participants, each response in the survey represents \(3^\circ\) of the circle.

Let's use this value to help us create a circle graph for a survey of \(120\) people.

A Survey of 120 Participants

\(120\) participants were asked to name a food that you would eat with the skin on.

Here are the frequency of their responses.

Response	Frequency
Chicken	\(30\)
Apple	\(50\)
Potato	\(25 \)
Peach	\(15\)

Recall we determine that

With \(120\) participants, each participant's response will represent \(3^\circ\) of the full circle.

\(30\) participants chose chicken. Since each response represents \(3^\circ\), we have \(30\) times \(3\), or \(90^\circ\) in total. So the response "Chicken" represents \(90^\circ\) of the circle. We can put this into our table.

Response	Frequency	Total Degrees of the Circle
Chicken	\(30\)	\(30 \times 3^\circ = 90^\circ\)
Apple	\(50\)
Potato	\(25 \)
Peach	\(15\)

We can use this same strategy for each of the categories.

• \(50\) participants chose apple. Since each response represents \(3^\circ\), we have \(50\) times \(3\), or \(150^\circ\) in total. So the response "Apple" represents \(150^\circ\) of the circle.
• Similarly, we can calculate that the response "Potato" will represent \(75^\circ\) of the circle.
• Finally, the response "Peach" will represent \(45^\circ\) of the circle.

We can now fill in our table.

Response	Frequency	Total Degrees of the Circle
Chicken	\(30\)	\(30 \times 3^\circ = 90^\circ\)
Apple	\(50\)	\(50 \times 3^\circ = 150^\circ\)
Potato	\(25 \)	\(25 \times 3^\circ = 75^\circ\)
Peach	\(15\)	\(15 \times 3^\circ = 45^\circ\)

Now that we know how many degrees of the full circle each category represents, we can use this information to create the circle graph.

Create a Circle Graph

We will keep our data for quick reference.

Response	Frequency	Total Degrees
Chicken	\(30\)	\(90^\circ\)
Apple	\(50\)	\(150^\circ\)
Potato	\(25\)	\(75^\circ\)
Peach	\(15\)	\(45^\circ\)

To start the circle graph, we draw a circle and mark the centre.

We next draw a line from the centre to the edge of the circle. Usually, we draw this first line straight up.

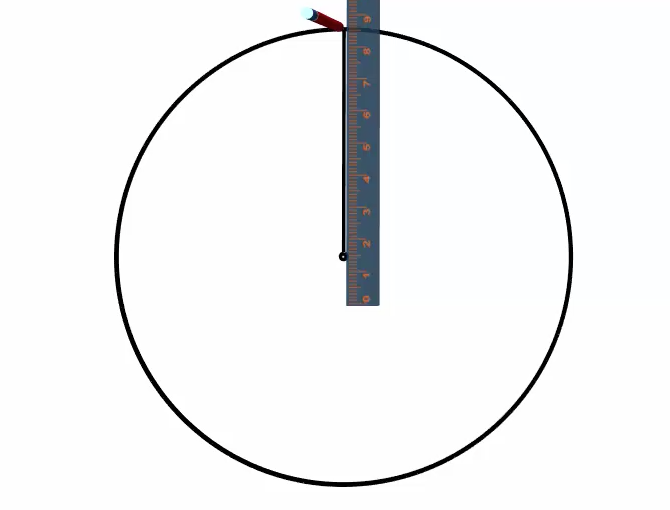
Recall that it is a good practice to start with the largest category and then order the categories from largest to smallest as you work around the circle in a clockwise direction. 

So lets start with the Apple category, since it is the largest. To measure the \(150^\circ\), we use our protractor and line up the \(0\) baseline with the centre of the circle and the line we have already drawn.

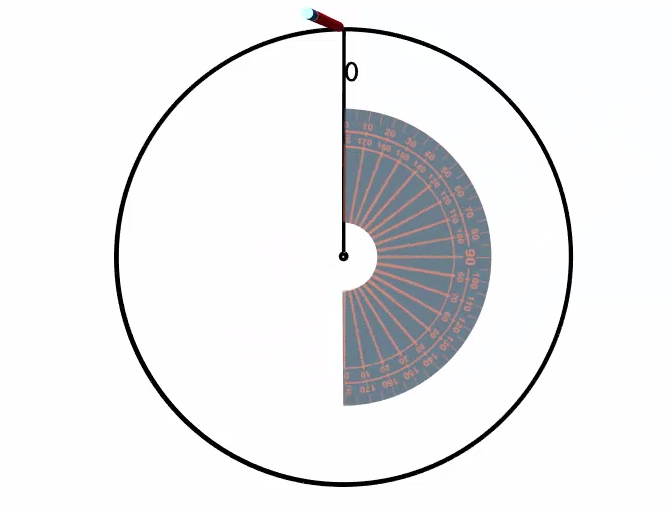
We then measure \(150^\circ\) and mark it with a point.

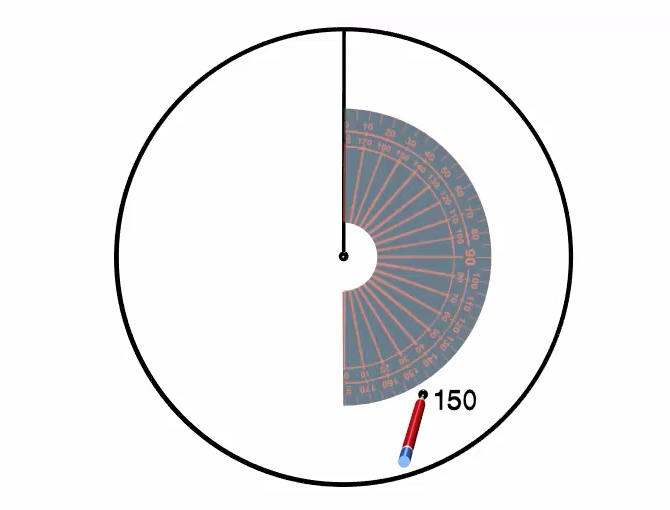
Using a ruler, we line up the centre with the point and draw a line from the centre to the edge of the circle to complete the \(150^\circ\) section of the circle.

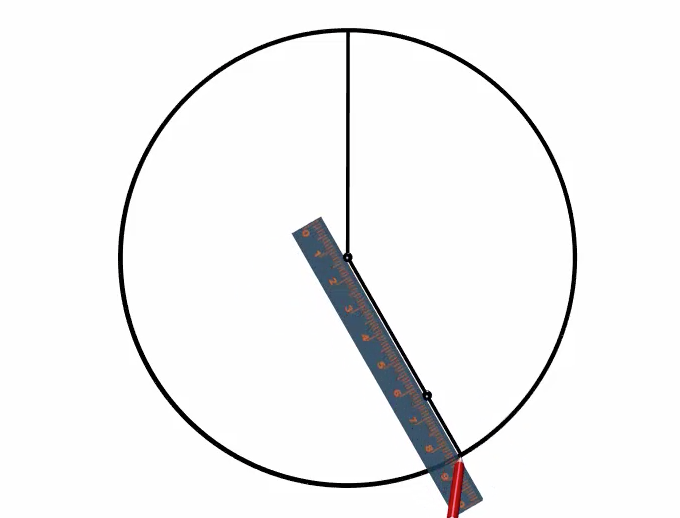
It is a good idea to label this section right away, so that we do not get confused which section of the circle corresponds to which category of our data. This section represents the category "Apple." And we can also label the \(150^\circ\) angle that we measured.

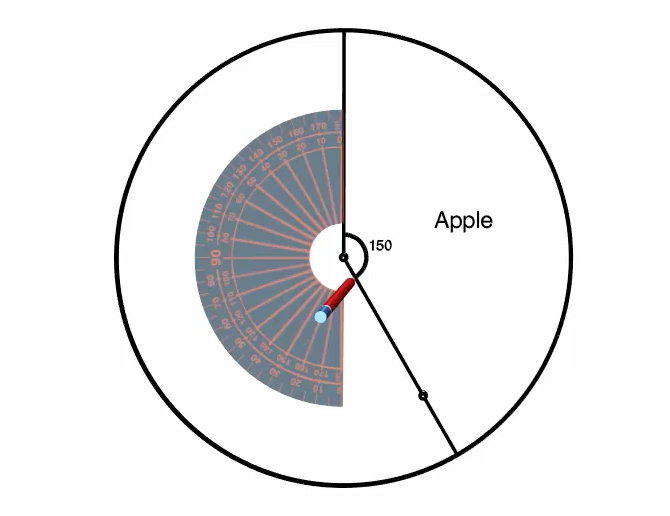
The next largest category is Chicken and it represents \(90^\circ\) of the full circle. Once again, we use our protractor, but this time we line up the \(0\) base line with the centre of the circle and the line that represents the end of the last section.

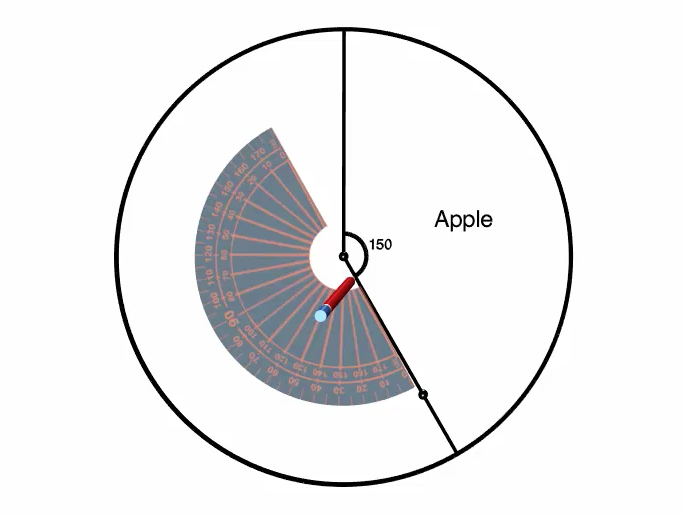
From here, we measure \(90^\circ\) and mark it with a point.

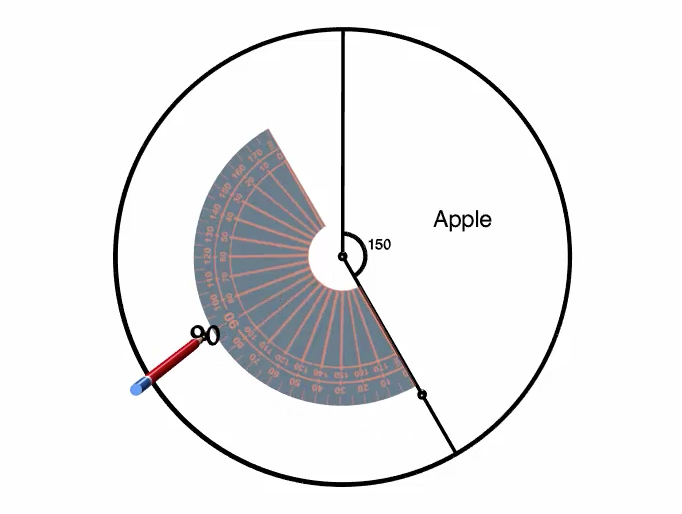
Using a ruler, we line up the centre with the point we just made and draw a line from the centre to the edge of the circle to complete the \(90^\circ\) section of the circle.

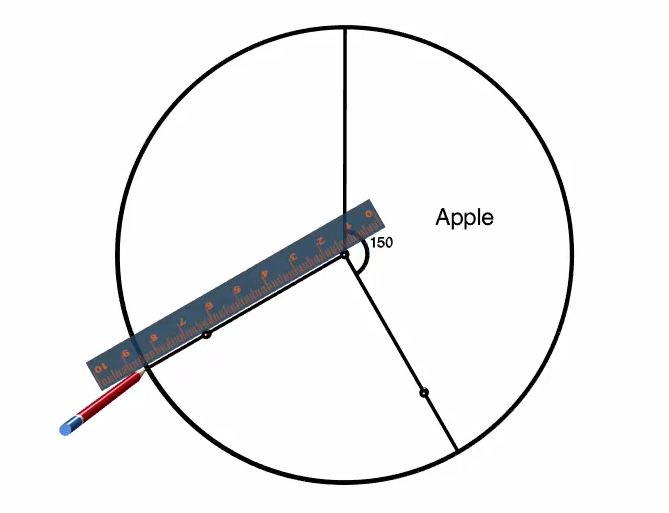
Once again, let's label this section right away with the category title "Chicken" and also the angle that we measured, \(90^\circ\).

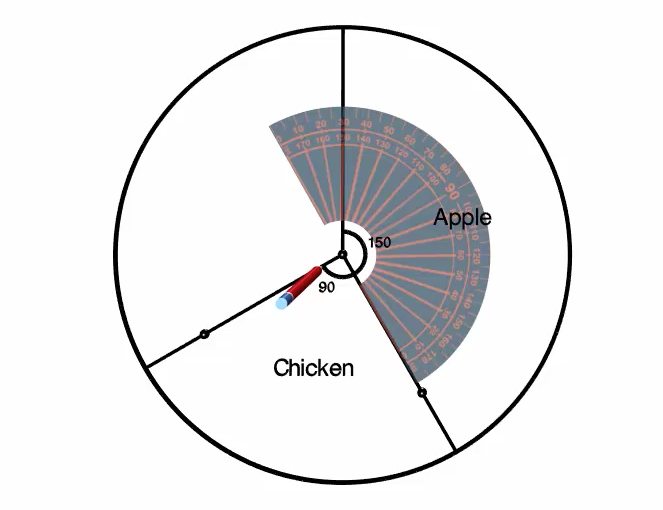
We can repeat the same process for the third category, Potato, which is a \(75^\circ\) section of the circle.

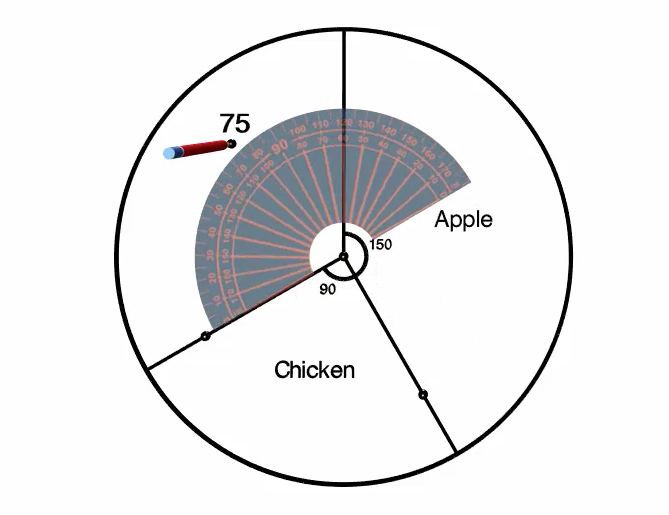
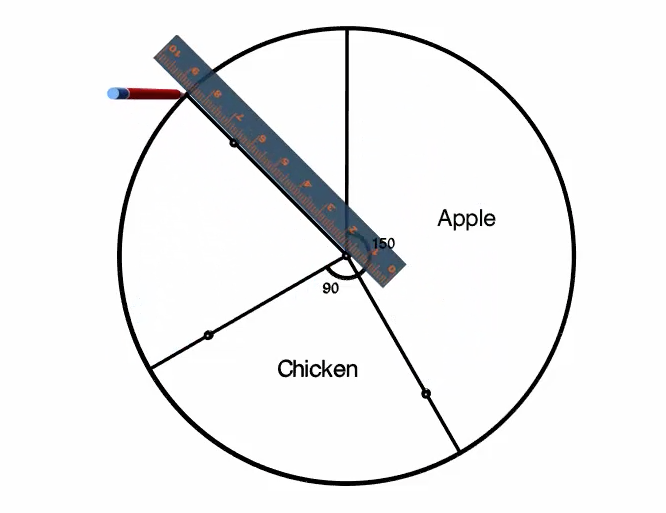
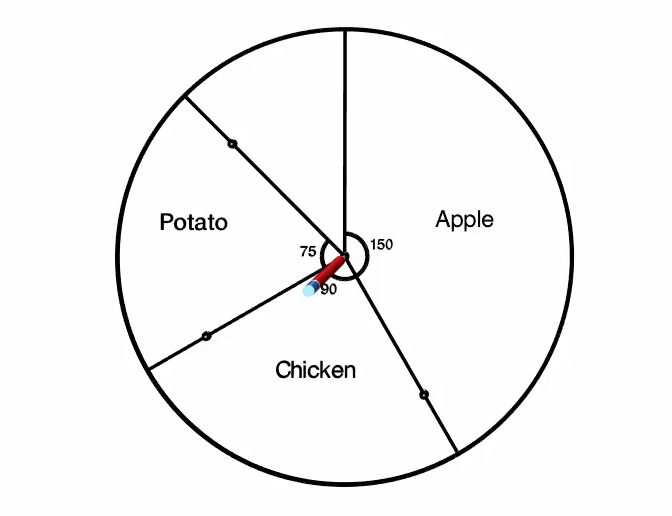
This should leave the fourth category, Peach, already measured out for us. We can add the label, "Peach" and use our protractor to confirm that the section remaining is indeed \(45^\circ\).

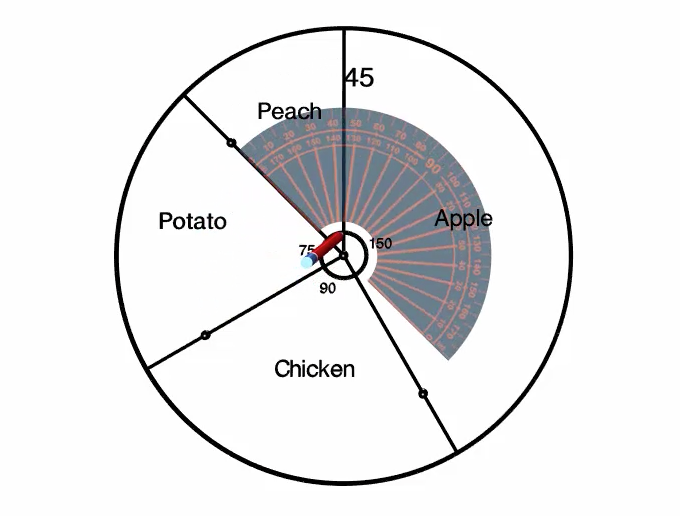
At this point, we have finished creating the circle graph. We can add an appropriate title, such as "Survey Responses" for food that you would eat with the skin on. And if we would like, we could add frequency or relative frequency data to the graph.

Survey Responses

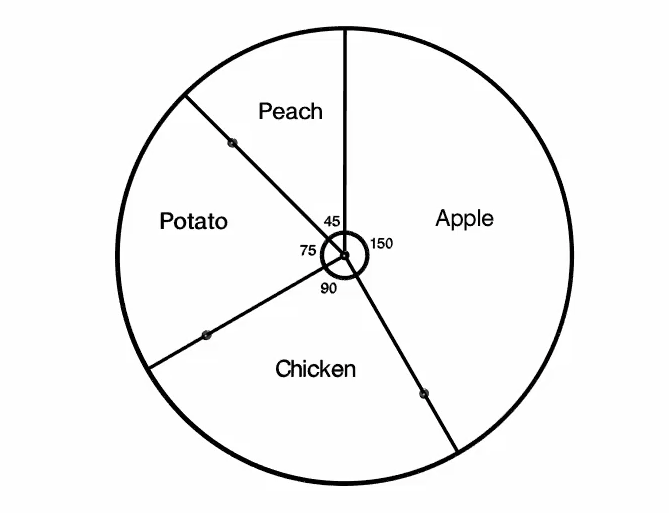
Created with Robocompass.com.  Author: University of Waterloo

Check Your Understanding 3

Question

\(90\) students were asked, "What is the best thing about school?" The following table shows the results. Complete the angle column in the table to create the circle graph. 

Response	Frequency	Section Angle
Friends	\(10\)
Teachers	\(47\)
Learning Things	\(33\)

Answer

Response	Frequency	Section Angle
Friends	\(10\)	\(40^\circ\)
Teachers	\(47\)	\(188^\circ\)
Learning Things	\(33\)	\(132^\circ\)

Feedback

Your section angles should add to \(360^\circ\). Since there are \(90\) students, that means each student's response represents \(360 \div 90 = 4^\circ\) of the circle.

The circle graph for the results would look like the following: 

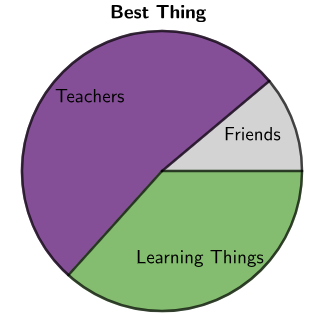
Created with GeoGebra. Author: University of Waterloo. CC BY-NC-SA 4.0. https://ggbm.at/KucbsgUj

Online Version

https://ggbm.at/KucbsgUj

Choosing the Right Graph

Choosing the Right Graph

Often data is represented in a graph to make the information easier to interpret.

Three commonly used graphs are circle graphs, bar graphs, and line graphs.

Line Graph

As mathematicians, we have a responsibility to choose an appropriate graph to represent a data set.

In the following examples, we will be given a data set. Our task will be to select an appropriate type of graph to represent the data set and justify why we made that choice.

Example 1

Solution

The type of sandwich topping is categorical data.

A circle graph is appropriate for categorical data and it works for this data.

The entire circle, in this case, represents all of the votes by the employees. On the graph, we can see that avocado is the largest section followed closely by spinach.

A bar graph is also appropriate for categorical data.

On this frequency bar graph we can easily see that avocado had the most votes and that it beat spinach by only \(1\) vote.

A line graph is best for numerical data and is not appropriate for this categorical data.

In summary, a circle graph or a bar graph would be appropriate for this categorical data set. I might lean towards making a bar graph in this case. The small numbers of this survey are easy to see in a bar graph. And a circle graph is a lot of effort to create, while not providing any visual gain for this data.

Example 2

Solution

A yes or no response is categorical data.

A circle graph is appropriate for categorical data and it works nicely for this data.

The entire circle, in this case, represents all of the responses by the employees. On the graph, it is easy to see that the answer no is slightly larger than half of the circle, which means that it received more than \(50\%\) of the responses.

A bar graph is also appropriate for categorical data.

On this frequency bar graph, we can easily see that the answer "No" received more responses. We could also create a relative frequency bar graph, which would provide the percent for each response.

A line graph is best for numerical data and is not appropriate for this categorical data.

In summary, a circle graph or a bar graph would be appropriate for this categorical data set. I might lean towards making a circle graph in this case, since it so nicely shows the simple data set and how close the vote was.

Example 3

Solution

Time is numerical data because it involves ordered numbers, specifically, the hour of the day.

A circle graph is best for categorical data. We could use each hour the data is collected as a category and create a circle graph of the hourly categories.

 

However, do you find it easy to see trends throughout the day in this graph? The structure of a circle graph makes noticing trends over time challenging, so the circle graph might not be the best option for this data.

Let's have a look at this data in a bar graph. The horizontal axis of the bar graph is the time in hours. And the vertical axis is the number of employees working at the shop. On this bar graph, we can see that the bars are taller during certain hours when there are more employees working, and the bars are shorter when there are fewer employees working.

A quick scan of this bar graph allows us to see trends in the number of employees at the shop throughout the day. However, there is a reason why this bar graph may not be the best option to display this data.

The separation between the bars makes us feel like each hour is a category on its own. For instance, there is no bar at 11:30 AM. But there would certainly be employees working at that time. We understand that the number of employees each hour is related to the hour before, since each employee would probably be working a shift that lasted many hours.

Let's have a look at a line graph for this same data. The line graph shows how the number of employees changes throughout the day.

Notice this line graph is similar in general shape to the bar graph. In fact, each data point on the line graph represents the top of one of the bars from the bar graph. While both the bar graph and line graph contain the same information, the lines connecting the points in the line graph help us to see that the number of employees from one hour to the next is related and suggests that we could have counted the number of employees at 11:30 AM. We just don't have that data.

In summary, we have shown that we can represent this data in a circle graph, bar graph, or line graph. For the reasons discussed, a line graph might be our best option.

Check Your Understanding 4

Question (Version 1)

The data below was collected at a weekend music festival.

Snack Type	Number Sold
Popcorn	\(250\)
Nachos	\(450\)
Peanuts	\(195\)
Fries	\(640\)
Pretzels	\(320\)

Which type of graph would best represent this data? Select all that apply. 

1. Bar Graph
2. Circle Graph
3. Line Graph

Answer (Version 1)

1. Bar Graph
2. Circle Graph

Feedback (Version 1)

Notice that this is categorical data. 

In general, categorical data is best displayed with either a bar graph or a circle graph. 

So, for this data, either option a) Bar Graph or option b) Circle Graph would be appropriate.

Question (Version 2)

The data below was collected at a weekend music festival.

Snack Type	Number Sold
4 PM	\(300\)
5 PM	\(650\)
6 PM	\(1300\)
7 PM	\(1800\)
8 PM	\(1100\)

Which type of graph would best represent this data? Select all that apply. 

1. Bar Graph
2. Circle Graph
3. Line Graph

Answer (Version 2)

1. Bar Graph

3. Line Graph

Feedback (Version 2)

Notice that this is numerical data. 

In general, numerical data is best displayed with either a bar graph or a line graph.

So for this data, either option a) Bar Graph or option c) Line Graph would be appropriate.

Take It With You

Here are two bar graphs of exactly the same data for internet browser speed scores.

1. Which graph do you think is the most fair representation of the data?
2. Why might the company that sells Browser B, choose to use Graph 1 in its sales advertisements?