Alternative Format

Try This

Graphs

The goal of a graph is to help the viewer quickly understand a data set. When we first look at a graph, we get an immediate reaction, or a general feeling, of what the graph is telling us.

For example, in Graph A, I get a general feeling that there are large differences between the numbers in each category.

Graph A

While in Graph B, the numbers in the categories appear to be relatively the same.

Graph B

The message communicated by each of these graphs does not immediately appear to be exactly the same.

However, these four graphs were all created with the exact same data set.

Decisions made during the creation of a graph can alter the message that a viewer of a graph will receive.

As critical thinkers, we want to be able to make use of graph features such as titles, labels, and scales to better inform ourselves of the story the graph is telling us and the underlying patterns in the data set.

Lesson Goals

• Inspect graphs with a focus on:
  • axis labels and scales,
  • structure and shape, and
  • graph type.
• Examine how certain choices in graph making can result in misleading graphs.

Throughout the lesson, we will look at examples of graphs that have been used in advertisements and media and critically think about how the graph was created to possibly give the viewer a specific message.

Try This!

Here are two graphs that represent the video game sales for a company over \(5\) years.

Which graph would a sales manager want to use to show the company's owner the improvements in sales over the last \(5\) years?

Explain why you chose that graph.

Think about this problem, then move on to the next part of the lesson.

Misleading Axes on Graphs

Axis Labels

Here's a bar graph from a lip balm advertisement. What message are the advertisers trying to convey with this graph?

On a first look at this bar graph, the bar for Brand B appears to be about \(4\) times as large as the bar for Brand A. This suggests to the viewer that Brand B is much better than the other brand.

However, as good graph inspectors, we should always consider the axis labels and make sure they are appropriate for the data. 

Notice that there is no label or scale on this graph's vertical axis.

We do not know what data this graph represents. This graph could represent the number of lip balms sold, the opinions of the owner of Brand B, or it could be the number of lawsuits each company has had. We have no idea. A graph without axes labels does not convey any meaningful information to the viewer.

Axis Scale

Here is a bar graph that was part of an article that compared newspaper sales between Company A and Company B. What message is the company trying to convey with this graph?

Source: Newspaper - Bytedust/iStock/Getty Images

My immediate reaction when viewing this graph is that Company A is clearly selling more newspapers than Company B. The bar for Company A appears to be about \(6\) times as large as the bar for Company B in the graph, suggesting that Company A sells about \(6\) times as many newspapers.

The axes labels are on the graph and seem to make sense.

However, as good graph inspectors, if we look closer at the scale, we notice that the vertical axis starts at \(450~000\). This is a very common tactic used by graph creators. By starting at \(450~000\) instead of \(0\) on the vertical axis, the difference between the two companies appears larger.

What would this graph look like if the vertical scale started at \(0\)? Let's have a look at that graph.

Notice that Brand A is still selling more newspapers, but now we see that the difference is actually not that large when compared to the total number of newspapers each is selling. What first looked like a difference of about \(6\) times as many is actually only \(1.07\) times as many, or an increase of about \(7\%\).

Changing the scale on the vertical axis of a graph can exaggerate the difference between data points.

This technique can be used by companies to make their products look much better than the competition's.

Try This Problem Revisited

Let's have a look at the Try This problem from earlier.

Solution

Graph A is an example of a graph with a vertical axis that does not start at \(0\).

Graph A

At first glance, this graph gives the impression that the sales at this company are drastically improving each year. Clearly, this company is making positive changes that are getting results. 

However, as good graph inspectors, we know that the vertical axis of the bar graph should start at \(0\).

Graph B represents the same data using a vertical axis that starts at \(0\).

Graph B

On this graph, we notice that while there is a small amount of growth, the number of sales year to year is basically staying the same.

While both of these graphs display the exact same data, each graph seems to be telling a different story about how the company did over the \(5\)-year period. The sales manager might use Graph A to give the impression that the sales staff have been improving significantly over the \(5\)-year period.

Axis Intervals

Here is a line graph that was used on a news show about gas prices. This graph shows the trend in gas prices over the last year. What message was the news show trying to convey with this graph?

My immediate reaction when I view this graph is that gas prices have been increasing slowly and steadily throughout the year.

Notice that both axes are labeled, and the vertical axis starts at \(0\). So as graph inspectors, we are happy with the scale on the vertical axis.

However, look carefully at the horizontal axis labels. Notice that the distance between last year and last month is the same as the distance between last week and today. However, these two time periods are not the same number of days.

When we create a number line, an important rule is that the scale must have consistent spacing. The same should apply for the scales on the axes of graphs.

The distance between values on an axis must be appropriate to the values of the data.

In this case, the horizontal values are last year, last month, last week, and today. The time spanned between each pair of these values is not equal. And therefore, they should not be equally spaced on the horizontal axis.

Let's recreate this graph by properly spacing this data on the horizontal axis.

This new graph tells a very different story about the gas prices. In this graph, the gas prices look to have a long, slow increase, followed by a drastic jump in the gas prices over the last \(30\) days.

A graph with incorrect spacing on either the horizontal or vertical axis can be misleading and can change the impression a viewer gets from the graph.

Check Your Understanding 1

Question (Version 1)

Is this graph misleading? 

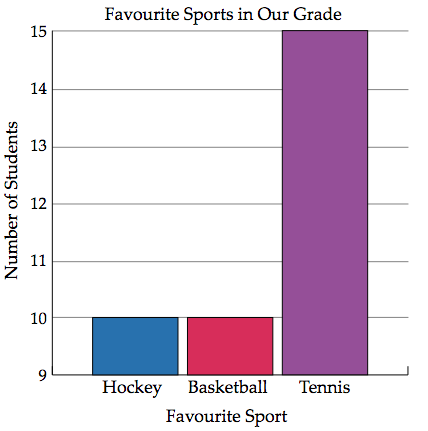
Answer (Version 1)

Yes, it is misleading.

Feedback (Version 1)

This graph is misleading.

We can see that vertical axis starts at \(9\), not \(0\). By doing this, it makes it look like tennis is much more popular than hockey and baseball. When we read the vertical axis, however, we notice that \(15\) students chose tennis, while \(10\) students chose chockey and \(10\) chose basketball, so in reality, tennis isn't that much more popular than hockey and basketball. Changing the scale on the vertical axis of a graph can exaggerate the difference between data points.

Question (Version 2)

Is this graph misleading? 

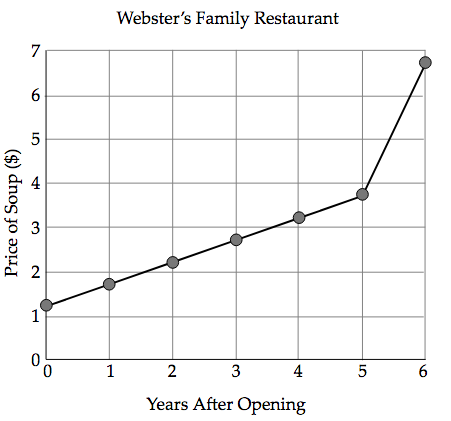
Answer (Version 2)

No, it is not misleading.

Feedback (Version 2)

This graph is not misleading.

We can see that the horizontal and vertical axes are both labelled. They also have scales starting at \(0\) that are evenly spaced. That tells us that the graph is not misleading. 

Misleading Graph Structure

The Shape of a Graph

Here are two graphs that represent the sales numbers for two employees at an appliance store.

Which person has improved their sales the most over the \(6\)-month period?

Take a moment and try this problem on your own.

Would it surprise you to find out that each of these graphs are of the exact same data? The data is just presented in a different way. While both graphs have the same labels and numbers on the vertical and horizontal axis, the first graph for Employee 1 is noticeably skinnier and taller.

Employee 1

This makes the lines in the graph look steeper, which in turn makes us feel like the salesperson has improved their sales more quickly.

The second graph for Employee 2 is wider and shorter.

Employee 2

This makes the lines in the graph look less steep, which in turn makes us feel like the salesperson has not improved their sales as quickly.

When the height or width of a graph is changed, the steepness of the lines in the graph also change.

As critical graph inspectors, we should consider the size and shape of the graph and how that might affect the story that is being communicated in the graph.

3-D Circle Graph

Computers can create cool graphs with a few clicks of a mouse. Here is a 3-D circle graph of the frequency of different numbers of syllables in English words. 

Syllables in English Words

We know that we don't need 3D to draw a circle graph. So why would anyone draw this type of graph?

One reason might be that it looks kind of cool. But is it also possible that it changes how we see the data?

Notice that the number of words with two syllables appears to be the largest slice of the circle graph.

However, as good graph inspectors, we would like to look at the relative frequency of each of these categories to make a better comparison.

Two-syllable words make up \(28\%\) of words, whereas three-syllable words make up \(29\%\) of all words. So even though the words with two syllables appears to be the largest slice of the circle graph, the words with three syllables slice was actually larger.

In an angled 3D circle graph, the angle of the circle creates a different perspective for the viewer. Often, slices at the front or back appear relatively larger than slices at the side of the circle. Since the three-syllable slice is along the side, it looks relatively smaller than it actually is.

This makes quick visual comparisons between the categories in an angled \(3\)-D circle graph are less reliable and possibly misleading.

Pictograph

Sometimes entertainment media likes to use pictographs because they're a fun way to communicate data. A pictograph uses pictures or symbols to represent frequencies for categorical data.

This pictograph represents popcorn sales at a movie theater over three days. The top of each popcorn image lines up with the appropriate value on the vertical axis.

Source: Popcorn - Octopus182/iStock/Getty Images

We can quickly see from the graph that the most popcorn was sold on Saturday, and the least was sold on Sunday.

Sometimes pictographs can be misleading when we compare the differences between categories.

Notice that while the height of the popcorn image changes appropriately for each day, the width of each popcorn image changes in size as well. When both the height and the width of the image changes, the visual size difference between categories is exaggerated. The number of popcorn sales on Saturday is only twice the number on Sunday. But the popcorn images make this difference appear to be much larger.

A better pictograph would use a consistent image and when necessary stack multiple images to represent larger values.

Check Your Understanding 2

Question

Which of the following graphs might Simon use to show each pie flavour is approximately equally popular?

Answer

Graph 2

Feedback

Simon must use Graph 2. 

We notice that the same data is used in both graphs, however, Graph 2 is a regular circular giraph, while Graph 1 is a 3D circle graph. The regular circle graph shows the size of each section clearly so would help Simon show that each pie flavour is approximately equally popular.

Misleading Graph Choices

Type of Graph

Here is a graph taken from a manager's report of beverage sales at a fast food restaurant for the month of April. What message is the manager trying to convey with this graph?

Take a moment and try this problem on your own.

When we first look at this graph, we get a general feeling that sales of beverages are increasing. However, as good graph inspectors, we always inspect the axes labels.

The horizontal axis is beverage size. Beverage size; small, medium, large, and extra large is categorical data. A line graph is generally not appropriate for categorical data. It is typically used to show trends over time.

Notice also that the beverage sizes are not even listed from smallest to largest. This makes us curious about why the sizes were not ordered logically.

A bar graph would be a much better and clearer choice for this data. Here is a bar graph of the same data with beverage sizes ordered.

The bar graph allows us to compare the numbers sold for each category of beverage size without making us feel that the sales were increasing over the month.

When examining graphs, we should consider the choice of graph type and how it may affect the story that is being communicated by the graph.

Type of Graph Continued

Circle graphs display a whole data set that can be subdivided into categories. The following circle graph shows support for each politician running in an upcoming election. 

Is this graph misleading? Why?

Politician Support

Take a moment and try this problem on your own.

When creating a circle graph, the circle represents the whole data set or \(100\%\).

When we add the relative frequencies provided in this graph, we get a total of \(70\%+63\%+60\%=193\%\), which is way over the maximum of \(100\%\) for a circle graph.

As good graph inspectors, we would like to see the original data for this graph so that we can understand if the graph is labeled incorrectly, or if the data was not appropriate for a circle graph. 

A circle used for a circle graph represents a whole data set and therefore the subdivided categories in the data cannot overlap each other. In this survey, the respondents were able to select their first choice and second choice of politician. When making the circle graph, both of these choices were used, which caused overlap between the categories.

A more informative graph would include just the first choices of each respondent. Here is a circle graph of the first-choice responses.

First Choice Support

This graph tells a much different story, as now politician two has the most support, while politician one has the least support.

As critical thinkers, we want to be able to examine graphs to better inform ourselves of the story a graph is telling us and the underlying patterns in the data.

Check Your Understanding 3

Question

Is the graph appropriate for the data?

Answer

Yes, it is appropriate.

Feedback

This graph is appropriate for the data.

We can see that the horizontal axis is the type of fruit, which is a categorical variable. Bar graphs are a clear way to display categorical data so this is an appropriate graph.

Take It With You

Here's the data for the percent of households with a landline phone over \(5\) years.

Year	Houses with Landline (\(\%\))
\(1\)	\(60\%\)
\(2\)	\(52\%\)
\(3\)	\(48\%\)
\(4\)	\(45\%\)
\(5\)	\(39\%\)

1. Imagine you work for a landline phone company. 
   Draw a graph to represent the data in a manner that minimizes the decrease in household landlines.
2. Imagine you work for a cell phone company.
   Draw a graph to represent the data in a manner that highlights the decrease in household landlines.