Area of a Trapezoid
Try This Problem Revisited
If the area of the parallelogram is \(33\) cm\(^2\), can you find the area of the trapezoid without using a formula?
Solution
First, we now know how the area of the parallelogram, which is \(33\) cm\(^2\), was calculated. We did so by multiplying the base, which is \(11\) cm, by the height, which is \(3\) cm.

Now to get back to the question, you may have noticed that the trapezoid has a lot in common with the left side of the parallelogram. So much so that it makes sense that we might try superimposing the two images as shown.

When we do this, we notice that the part of the parallelogram that's left unshaded is actually a second copy of the given trapezoid, just upside down.
The area of the given trapezoid is \(\dfrac{1}{2}\) the area of the parallelogram.
The area of the parallelogram is \(33\) cm\(^2\).
Therefore, the area of the trapezoid is
\(\dfrac{1}{2} \text{ of } 33 = 16.5 \text{ cm}^2\)
Formula for the Area of a Trapezoid
To determine the formula for the area of any trapezoid, we generalize the observation from the Try This problem. To determine the area of a trapezoid, we must know the perpendicular height, labelled \(h\), and the lengths of the two parallel sides labelled \(a\) and \(b\).

When we place two identical trapezoids together as shown, we get a parallelogram.

The area of the trapezoid is \(\dfrac{1}{2}\) the area of the corresponding parallelogram.
To calculate the area of this parallelogram, we would multiply the length of the base, which is \(a+b\), by the height \(h\).
Area of the parallelogram \(= (a+b)\times h\)
A trapezoid has two parallel sized of lengths \(a\) and \(b\) and a height \(h\). The area of the trapezoid can be calculated using the equation
\(A=\dfrac{1}{2}(a +b) h\)

Example 7
Calculate the area of the following trapezoid.

Solution
The two parallel sides are \(6\) m and \(12\) m in length. The perpendicular distance between them is \(4\) m.
\(\begin{align*} A &= \dfrac{1}{2}(a+b)h \\ &\; = \dfrac{1}{2}(6+12)(4) \\ & \; = \dfrac{1}{2}(18)(4) \\ & \; = (9)(4) \\ & \; = 36 \end{align*}\)
Therefore, the area of the trapezoid is \(36\) m\(^2\).
Check Your Understanding 6
Question
Calculate the area, in mm\(^2\), of the trapezoid shown below.
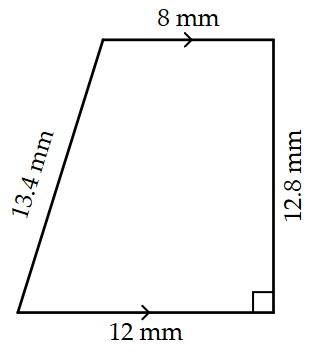
Answer
\(128\) mm\(^2\)
Feedback
Notice the two parallel sides are \(8\) mm and \(12\) mm in length, and the height is \(12.8\) mm. Using the formula for the area of a trapezoid, we have:
\(\begin{align*} A & = \dfrac{1}{2} (a+b)h \\ & = \dfrac{1}{2} (8+12)(12.8) \\ & = \dfrac{1}{2} (20)(12.8) \\ & = (10)(12.8) \\ & = 128\end{align*}\)
Therefore, the area of the trapezoid is \(128\) mm\(^2\).
Summary of Area Formulas
Let's now take a moment to recap all of the formulas that we saw in this lesson. We begin by reviewing the formula for the area of a rectangle.
Rectangle
\(A=l\times w\)

Then we showed that the area of a parallelogram can be calculated by multiplying its base by its height.
Parallelogram
\(A = b\times h\)

Triangle
\(A= \dfrac{1}{2}(b\times h)\)

We also learned how to find the area of a trapezoid if we know the lengths of the parallel sides and the height.
Trapezoid
\(A = \dfrac{1}{2}(a+b)\times h\)

In the following Check Your Understanding, practice using all of these formulas to solve area problems.
Check Your Understanding 7
Question
Calculate the area, in m\(^2\), of the triangle shown below.
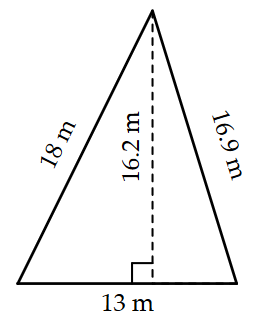
Answer
\(105.3\) m\(^2\)
Feedback
Notice the base of the triangle is \(13\) m and the height is \(16.2\) m. Using the formula for the area of a triangle, we have:
\(\begin{align*} A & = \dfrac{1}{2} (b\times h) \\ & = \dfrac{1}{2} (13\times 16.2) \\ & = \dfrac{1}{2} (210.6) \\ & = 105.3 \end{align*}\)
Therefore, the area of the triangle is \(105.3\) m\(^2\).
Take It With You
The following pair of parallel lines are drawn so that they are \(4\) cm apart.

A rectangle, triangle, parallelogram, and trapezoid are drawn so that every vertex is on a parallel line.
If they are all equal in area, what do you know about the dimensions of each polygon?