Alternative Format

Try This

3D Objects Around You

Cereal box manufacturers calculate the quantity of materials they will need for packaging so they can estimate the packaging costs. 

Estimate the packaging costs.

Knowing the surface area of a tent will allow you to calculate how many cans of waterproofing spray would be needed to coat the outside surfaces of the tent.

Calculate how many cans of waterproofing spray are needed.

Furthermore, knowing the surface area of a hay bale helps farmers estimate the quantity of plastic wrapping to buy when preparing the hay for storage. 

Estimate the quantity of plastic wrapping to buy.

In each of these examples, the surface area of an object is used to make a decision. 

Sources: Cereal - PeopleImages/E+/Getty Images; Tent - ChiccoDodiFC/iStock/Getty Images; 
Hay Bale - ligora/iStock/Getty Images

Lesson Goals

• Visualize the surface area of a 3D solid.
• Calculate the surface area of various objects.
• Solve word problems involving surface area.

Try This!

A tent has the shape of a triangular prism, with dimensions as shown. 

 

Waterproofing spray is used to cover the outside surfaces of the tent.

If \(1\) can of waterproofing spray covers \(3\) m\(^2\), how many cans are needed to spray all of the outside surfaces of the tent (including the bottom)? 

Think about this problem, then move on to the next part of the lesson.

Nets of 3D Objects

2D Shapes vs. 3D Objects

Recall that a two dimensional or 2D shape is a planar figure, such as a rectangle, which has length and width. On the other hand, a three dimensional or 3D object is a solid, such as a rectangular prism, which has a length, a width, and a height.

Net of a Rectangular Prism

Consider the following box. Looking at the structure of the box, we see that it is a prism with 6 rectangular faces. More specifically, we call it a rectangular prism. For the purpose of this explanation, we're going to think of the box as being empty. 

Rectangular prism

Now imagine cutting along the highlighted edges of this box.

Then unfold it so that it lays flat. The result is a 2D composite shape. We call this 2D shape the net of the prism.

Net of the rectangular prism

Now if we want to find the surface area of the box, then we want to find the area of the cardboard used to build the box. Using our diagram, we see that the surface area of the box is equal to the area of the net. We can create nets for many 3D objects. And these nets can help us to visualize an object surface area.

In the following investigation, explore the nets of some common 3D objects.

Explore This

Description

Explore 3D objects and their nets.

Cube and Its Net

Rectangular Prism and Its Net

Triangular Prism and Its Net

Created with GeoGebra. Author: University of Waterloo. CC BY-NC-SA 4.0. https://ggbm.at/c6szzmvb

Online Version

https://ggbm.at/c6szzmvb

Summary of Explore This

The net of a 3D object is a composite shape formed using the faces of the object. 

 Let's practice drawing nets.

Example 1

Solution

Let's start by first looking at the faces of the solid. We see two identical triangular faces.

We also see three rectangular faces, two of which are also identical.

Therefore, we know that any net will be made up of these five shapes.

To create a net, we can cut along the top edge as well as the two equal sides of each triangular face. 

Unfolding, we get the following net.

To label the side lengths, we need to look back to the original solid that we were given. Specifically, let's start by looking at the edge labelled \(3\) cm on that front triangular face. On the net, the two highlighted sides form this edge of the solid. Therefore, both of these sides are \(3\) cm in length.

The same argument can be made from the sides that form the other \(3\) cm edges of this prism.

And so we can go ahead and mark that these sides are also equal to \(3\) cm, using hashmarks.

 

The base of each triangle is \(5\) cm, so we can now go ahead and label these on the net.

Finally, the remaining side lengths are \(10\) cm as they are equal to the length of the prism.

Example 1 — Alternate Solution

Alternate Solution

I'll take a moment to note that your 2D net could have had a different arrangement of faces. To give you an alternative solution, if you cut along a different set of edges, you would get the following net or perhaps another different one yet.

If you follow the same idea of matching sides to form edges, the side lengths on the net would be as shown.

Check Your Understanding 1

Question

Consider the net below. When the net is folded up, which of the following prisms will it create, if any?

1. Cube
2. Rectangular Prism
3. Triangular Prism
4. None of the above

Answer

1. Cube

Feedback

The net has \(6\) square faces, just like a cube.

When we fold this net up, we can see that it will indeed create a cube.

Calculating Surface Area

Example 2

Recall that the net of a 3D object is a composite shape. For example, consider the following solid and it's net.

Notice that the net is a composite shape composed of \(6\) rectangles, specifically, the \(6\) rectangular faces of the solid. Since we know how to find the area of composite shapes, we can find the area of this net. And this will represent the surface area of the solid.

Solution

The first thing I want to do is to reiterate that the net is composed of \(6\) rectangles. It's also helpful to recognize that some of these rectangles are identical to each other. In fact, there are three different pairs. This observation simplifies the number of area calculations that we have to do, because we can calculate the area of one rectangle from each pair and then multiply this value by \(2\).

Since the area of the net is equal to the surface area of the rectangular prism, we write that the surface area is going to be equal to \(2\) times the area of Rectangle 1, plus \(2\) times the area of Rectangle 2, plus \(2\) times the area of Rectangle 3. We now need to calculate the area of each rectangle. 

We now have an expression that represents the surface area of the prism. 

\[\begin{align*} SA &= 2\times A_{rec~1} \class{timed in6}{\;+ 2\times A_{rec~2}} \class{timed in7}{\; + 2 \times A_{rec~3}} \\ &\; \class{timed in10}{= 2\times 8 \;+\;} \class{timed in12}{ 2\times 14 \;+\;} \class{timed in14}{ 2 \times 28} \\ &\; \class{timed in16}{= 100} \end{align*}\]

Thus, the surface area of the prism is \(100\) cm\(^2\).   

Example 3

Solution

Looking at this triangular prism, we see that there are \(5\) faces -- \(2\) triangular faces and \(3\) rectangular faces. Since this is a prism, we know that the \(2\) triangular faces are identical.

The surface area of this prism is equal to the sum of the area of the \(5\) faces. If you need to draw the net to visualize this, you can continue to do so. Or you can start to work directly from the 3D diagram of the prism that you're given.

The surface area of the triangular prism is going to be equal to \(2\) times the area of the triangular face plus the area of Rectangle 1 plus the area of Rectangle 2 plus the area of Rectangle 3. We have to go ahead and calculate the area of each face.

We're going to go ahead and substitute this information into the equation for the surface area. We now have an expression that we can evaluate to find the surface area of the prism.

\[\begin{align*} SA &\; \class{timed in6}{= 2\times A_{tri}} \class{timed in7}{ \;+\; A_{rec~1}} \class{timed in8}{ \;+\; A_{rec~2}} \class{timed in9}{ \;+\; A_{rec~3}} \\ &\; \class{timed in12}{= 2 \times 6 +\;} \class{timed in14}{35 +\;} \class{timed in16}{ 28 + 21} \\ &\; \class{timed in18}{= 96} \end{align*}\]

Thus, the surface area of the prism is \(96\) m\(^2\).

Check Your Understanding 2

Question

Calculate the surface area, in mm\(^2\), of the triangular prism below.

Answer

\(231\) mm\(^2\)

Feedback

This triangular prism has \(2\) identical faces and \(3\) rectangular faces.

The surface area of the triangular prism is

\(SA = 2 \times A_{tri} + A_{rec1} + A_{rec2}+A_{rec3}\)

Calculating the area of each face gives us

Therefore,

\(\begin{align*} SA &= 2 \times 13.5 + 60 +72 + 72 \\ & = 231\end{align*}\)

Thus, the surface area of the triangular prism is \(231\) mm\(^2\).

Word Problems

Try This Problem Revisited

Solution

Step 1: Calculate the Surface Area of Tent

To determine the quantity of waterproofing spray needed, we must determine the surface area of the tent using the following equation.

\(\begin{align*} SA &= 2\times A_{front} + 2 \times A_{side} + A_{bottom} \\ &\; \class{timed in3}{= 2 \times (0.7) } \class{timed in4}{\;+\; 2 \times (2.52)} \class{timed in5}{ \;+\; 2.94} \\ &\; \class{timed in6}{= 9.38} \end{align*}\)

The total surface area of the tent is \(9.38\) m\(^2\). 

Step 2: Determine Number of Cans of Spray 

\(1\) can of waterproofing spray covers \(3\) m\(^2\), and

\(9.38 \div 3 \approx 3.13 \)

What this tells us is that we need \(3.13\) cans. But clearly, we can't buy a partial can.

Therefore, \(4\) cans of waterproofing spray would need to be purchased.

Example 4

Solution

Step 1: Calculate the Surface Area of Composter

To determine the total cost of the materials, we must first determine the surface area of the composter. Notice that the sides of the composter are trapezoids, and so this composter can be thought of as a trapezoidal prism. As such, we can use the following equation to calculate the surface area.

\(SA = 2\times A_{side} + A_{top} + A_{bottom} + A_{front} + A_{back}\)

We summarize this as follows:

\[\begin{align*} SA &= 2\times A_{side} + A_{top} + A_{bottom} + A_{front} + A_{back} \\ & \;\class{timed in3}{= 2 \times 0.625} \class{timed in4}{\;+\; 2.1} \class{timed in5}{ \;+\; 1.5 } \class{timed in6}{ \;+\; 3} \class{timed in7}{ \;+\; 4.5} \\ &\; \class{timed in8}{= 12.35} \end{align*}\]

The total surface area of the composter is \(12.35\) m\(^2\).

Step 2: Determine Cost of Materials

We know that materials cost \($9.98\) per m\(^2\).

Since

\[12.35 \times 9.98 =  123.253\]

We can conclude that it will cost approximately \($123.26\) in materials to build the composter.

Check Your Understanding 3

Question

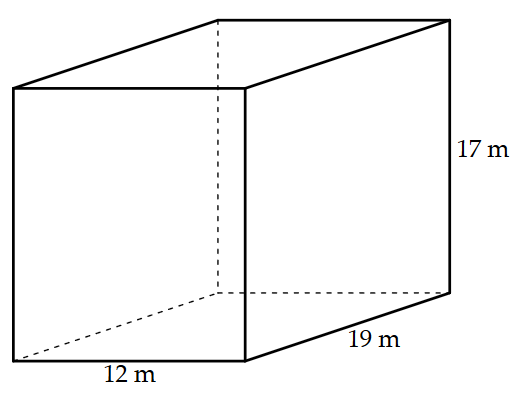
One type of paint requires \(1\) L of paint to cover \(10\) m\(^2\). How much paint, in L, is needed to paint the outside of the following structure?

Answer

\(151\) L

Feedback

Step 1: Calculate the surface area of the rectangular prism

This rectangular prism has \(2\) identical rectangular faces on the ends, \(2\) identical rectangular faces on the sides, and \(2\) identical rectangular faces on the top and bottom.

The surface area of the rectangular prism is

\(SA = 2 \times A_{rec1}+2\times A_{rec2} + 2\times A_{rec3}\)

Calculating the area of each face gives us

Therefore,

\(\begin{align*}SA & = 2 \times 204 + 2 \times 323 + 2 \times 228 \\ & = 1510 \end{align*}\)

Thus, the surface area of the rectangular prism is \(1510\) m\(^2\).

Step 2: Calculate the amount of paint needed

\(\begin{align*}\text{amount of paint needed } & = 1510 \div 10 \\ = 151 \end{align*}\)

Therefore, you would require \(151\) L of paint.

Take It With You

The length, width, and height of a rectangular prism are all that we require to calculate the surface area.

How does the surface area of a rectangular prism change in the following cases?

1. One dimension is doubled or tripled?
2. Two dimensions are doubled or tripled?
3. All three dimensions are doubled or tripled?