Composite Solids
Example 6
A composite solid is made up of two or more prisms joined together.
Find the volume of the following composite solid.

Solution
Just like we did when finding the area of composite shapes, we find the volume of composite solids by decomposing the solid into simpler solids for which we have simple volume formulas.
Notice that this solid is composed of a smaller rectangular prism where the length is \(3\) m, width is \(2\) m, and height is \(4\) m.

The larger rectangular prism has length \(3\) m, width \(3\) m, and height \(6\) m.

The volume of the total solid is equal to the volume of the small prism plus the volume of a large prism.
The volume of the smaller prism is equal to the area of its base times its height.
\(\begin{align*} V_{small} &\; \class{timed in6}{= (3\times 2) \times 4 }\\ &\; \class{timed in7}{= 6 \times 4} \\ &\; \class{timed in7}{= 24} \end{align*}\)
Similarly, the volume of the larger prism is equal to the area of its base times its height.
\(\begin{align*} V_{large} &\; \class{timed in10}{= (3\times 3) \times 6 }\\ &\; \class{timed in11}{= 9 \times 6} \\ &\; \class{timed in11}{= 54} \end{align*}\)
We now look at the equation for the total volume and evaluate:
\[\begin{align*} V_{total} &= V_{small} + V_{large} \\ &\; \class{timed in8}{= 24 \;+\;} \class{timed in13}{54} \\ &\; \class{timed in14}{= 78} \end{align*}\]
The volume of the composite solid is \(78\) cm\(^3\).
Check Your Understanding 6
Question
Find the volume of the following composite solid.
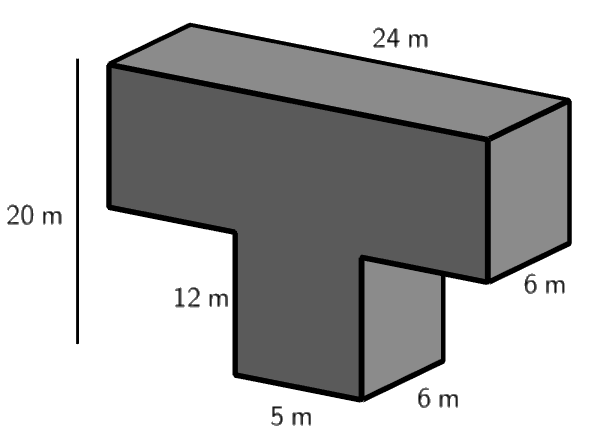
Answer
\(1512\) m\(^3\)
Feedback
Try dividing the shape as shown and calculating the volume of each part separately.
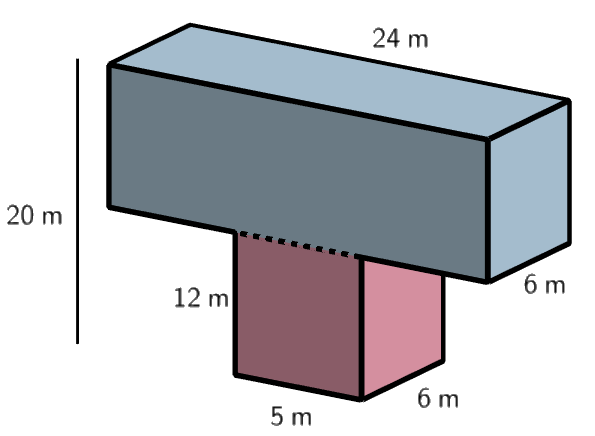
\(\begin{align*}V_{top} & = 24 \times 6 \times 8 \\ & = 1152\end{align*}\)
\(\begin{align*}V_{bottom} & = 5\times 6 \times 12 \\ & = 360 \end{align*}\)
\(\begin{align*}V_{total} & = V_{top} + V_{bottom} \\ & = 1152+360 \\ & = 1512 \end{align*}\)
Thus, the volume is \(1512\) m\(^3\).
Created with GeoGebra. Author: University of Waterloo. CC BY-NC-SA 4.0. https://ggbm.at/BDK497G7
Online Version
https://ggbm.at/BDK497G7
Try This Problem Revisited
We can also use our knowledge of composite solids to solve problems involving capacity. To see this, let's revisit to try this problem.
The space inside the glass jar has dimensions as marked on the diagram and a single jellybean has a volume of \(3.5\) cm\(^3\).
Estimate how many jelly beans the jar can hold.

Solution
Looking at this jar notice that it can be thought of as a composition of two identical trapezoidal prisms. We can find the capacity of the jar by finding the volume of these two prisms.
\(\begin{align*} V &= 2 \times V_{trapezoidal~prism} \\ & \; \class{timed in4}{= 2 \times \left( \dfrac{1}{2} (5+11)(4) \times 25 \right)}\\ & \; \class{timed in5}{= 2 \times (32) \times 25} \\ & \; \class{timed in5}{= 1600 } \end{align*}\)

The capacity of the jar is \(1600\) cm\(^3\).
Now that we know the capacity of the jar, our second step is to determine how many jelly beans will fit inside. We can do this by dividing the capacity of the jar by the volume of one jelly bean. If each jelly bean has a volume of \(3.5\) cm\(^3\) and
\[1600 \div 3.5 \approx 457.14\]
we would estimate that the jar could hold about \(457\) jelly beans.
Now, an important question to consider if you were actually submitting a guess is would you actually expect the jar to hold \(457\) jelly beans? Think about why the number in the jar should be slightly less than that.
Try This Problem Revisited — Continued
The space inside the glass jar has dimensions as marked on the diagram and a single jelly bean has a volume of \(3.5\) cm\(^3\). Estimate how many jelly beans the jar can hold.

Alternate Solution
Now, the try this problem is interesting. Because you can actually approach finding the capacity of the jar in a different way. Alternatively, you can view the base of the jar as a composite shape because it's a hexagon, which we can see as two identical trapezoids.
\(\begin{align*} V &= A_{base} \times h \\ &\; \class{timed in3}{= \left( 2 \times \dfrac{1}{2}(5+11)(4) \right) \times 25 }\\ &\; \class{timed in3}{= 2 \times (32) \times 25} \\ &\; \class{timed in3}{= 1600 } \end{align*}\)

The capacity of the jar is \(1600\) cm\(^3\).
Notice that even though we thought about this problem in a different way, the algebra actually works out to be quite similar.
Check Your Understanding 7
Question
The space inside a cardboard box is in the shape of a rectangular prism. It has a length of \(35\) cm, a width of \(35\) cm, and a height of \(24\) cm. A single golf ball has a volume of approximately \(39.4\) cm\(^3\).
We want to estimate how many golf balls the cardboard box can hold. Which of the following estimates is most reasonable?
- \(373\)
- \(1492\)
- \(2238\)
- \(746\)
Answer
- \(746\)
Feedback
Step 1: Calculate the capacity of the cardboard box.
\(\begin{align*} V & = 35 \times 35 \times 24 \\ & = 29~400 \end{align*}\)
Thus, the capacity of the cardboard box is \(29~400\) cm\(^3\).
Step 2: Estimate the number of golf balls.
Each golf ball has a volume of approximately \(39.4\) cm\(^3\), so
\(29~400 \div 39.4 \approx 746\)
We would estimate that the cardboard box could hold about \(746\) golf balls.
Take It With You
A cooler has an advertised capacity of \(17\) L.

You measure the dimensions of the cooler and determine that the capacity should be about \(40\) L.
Explain why the advertised capacity is different than what you calculated.