Alternative Format

Try This

Representing 3D Objects in 2D

Drawing a picture is one way to help solve a problem or to help explain a situation. When trying to find the volume of a prism, it was helpful to consider a sketch of the 3D object. 

Sketch

\(V=A_{base}\times h\)

When trying to find the surface area of a prism, it was helpful to consider a net. 

Net

\(SA = 2\times A_{triangle} + 3\times A_{rectangle}\)

Sketching a 3D object in 2D can distort some of the shapes. Look at the given diagram of a triangular prism. Can you tell that the triangular faces are equilateral? On the other hand, a net tells us information about the surface of an object that leaves us to figure out what the object actually looks like. The 3D sketch and the net are just two ways that we can draw a 3D object on paper. But there are other ways as well.

2D Views

For example, engineers design tools, fixtures, and machinery. When designing, they create both a 3D sketch as well as 2D drawings to represent the different views, such as the front view or the top view. The 3D sketches of models are easy to understand and are useful in visualizing the entire design. Different 2D views, such as top view or a front view, allow you to see details of the design.

Specifically, engineers can communicate dimensions and sizes which cannot be easily shown on a 3D sketch. The 2D drawings on screen are of a pump commonly used for oil drilling.

Source: Drilling Pump - cherezoff/iStock/Getty Images

These are much more complex than the 2D drawings we will be doing in this lesson. But they give you an idea of a real application of topics that we're about to cover.

Lesson Goals

• Recognize and sketch different 2D views of a 3D object.
• Sketch a 3D object given different 2D views of the object.

Try This!

Given the following top, front, and side views of a solid, sketch the 3D object on the triangular dot paper provided.

Triangular Dot Paper

Think about this problem, then move on to the next part of the lesson.

Drawing Rectangular Prisms

Square vs. Triangular Dot Paper

Consider a section of one centimetre square dot paper. Pick any dot.

The dots beside it are centimeter away. Similarly, the dots above and below it are also centimetre away. 

Square Dot Paper

However, the diagonal dots are more than one centimetre away. Because the distances between dots are not necessarily equal, it's hard to get the right proportions when trying to sketch prisms on this type of paper.

 Tp solve this problem, we use triangular dot paper, also called isometric dot paper. 

On one centimetre triangular dot paper, the distance between any two adjacent dots is equal to one centimetre. 

Triangular Dot Paper

This feature helps us to accurately draw prisms with more ease. Let's start by drawing the simplest prism, a cube.

Drawing a Cube on Triangular Dot Paper

Consider a cube with one centimetre sides. We want to draw this cube on triangular dot paper.

To do this, we're going to zoom in on both the cubed and the triangular dot paper so that our diagrams are larger and more clear.

To start, pick a point of reference, label it \(P\) on the cube, and then mark this point of reference on the dot paper.

We call this diagram an isometric drawing of the cube.

You can try to draw the same cube on square dot paper, but it will be more challenging to get the size to be in the same proportion. What's also interesting is that cubes can be combined to form rectangular prisms and other composite solids, which can also be drawn on triangular dot paper. Let's see an example of that right now.

Example 1

Solution

Using the same strategies that we practice for drawing a cube, you should get the following isometric drawings for these two objects. Check your drawings to make sure that they are the same as the ones on screen.

Check Your Understanding 1

Question

Draw the 3D object on the triangular dot paper using the point \(P\) as a point of reference.

Answer

Check that the image you drew is the same size and shape as the answer shown.

Created with GeoGebra. Author: University of Waterloo. CC BY-NC-SA 4.0. https://ggbm.at/eKgVuUHE

Online Version

https://ggbm.at/eKgVuUHE

Example 2

Solution

Remember that on one-centimetre triangular dot paper, the distance between any two adjacent dots is \(1\) cm. Using the fact that the distance between two adjacent dots is \(1\) cm, you should get the following isometric drawings for these two objects.

Check your drawings to make sure that they are the same as the ones onscreen.

Check Your Understanding 2

Question

Draw the 3D object on the triangular dot paper.

Answer

Check that the image you drew is the same size and shape as the answer shown. Your drawing might be rotated or in a different location on the grid than the answer.

Created with GeoGebra. Author: University of Waterloo. CC BY-NC-SA 4.0. https://ggbm.at/ffqt9McK

Online Version

https://ggbm.at/ffqt9McK

Sketching 2D Views

Top, Front, and Side Views

Now that we're able to draw 3D objects on triangular dot paper, let's think about how we can use our isometric drawings to make 2D drawings. Specifically, we're going to focus on the top, front, and side views of an object. 

Consider the following isometric drawing of a prism. The top, front, and side of the prism are indicated.

We can use square dot paper (or grid paper) to draw each view of the prism.

These diagrams represent the top, front, and side view of the prism.

Check Your Understanding 3

Question

Draw the front view of the prism on the square dot paper.

Answer

Check that the image you drew is the same size and shape as the answer shown. Your drawing might be rotated or in a different location on the grid than the answer.

Created with GeoGebra. Author: University of Waterloo. CC BY-NC-SA 4.0. https://ggbm.at/S8QKK5jX

Online Version

https://ggbm.at/S8QKK5jX

Example 3

Solution

At first glance, I think it's more difficult to draw the different perspectives of this solid, because somehow, we have to show the change in depth.

To explain what I mean by that, consider the top view of this solid. When we look at this solid from the top, we see that the shape takes up the space of a \(1\) by \(4\) rectangle. But this is not a rectangular face like we saw with prisms.

Top View

Instead, we notice that the first unit square is on a different level than the last \(3\) unit squares. To show this change in depth, we can draw a line.

Next, we can look at the front view. This is more like the previous examples, and we draw the front view as an L-like shape with a height of \(2\) units and a length of \(4\) units.

Front View

Finally, when we look at the side view, we see that the shape takes up the space of a \(2\) by \(1\) rectangle. But again, notice that not all parts are on the same level. 

Side View

To show the change in depth, we can draw a horizontal line where the depth changes. 

Take a few moments to compare these 2D drawings of the top, front, and side views to the 3D object.

Check Your Understanding 4

Question

Draw the front view of the composite solid on the square dot paper.

Answer

Check that the image you drew is the same size and shape as the answer shown. Your drawing might be rotated or in a different location on the grid than the answer.

Created with GeoGebra. Author: University of Waterloo. CC BY-NC-SA 4.0. https://ggbm.at/A6nFGJZ9

Online Version

https://ggbm.at/A6nFGJZ9

Sketching 3D Views

Manufacturing 3D Objects From 2D Sketches

Sometimes 2D drawings are all that companies provide for instructions of how to manufacture a 3D object. Some companies must rely on 2D drawings because they might not be able to afford the latest in 3D modelling systems. After all, they do require a lot of hardware, software, and training. Architectural firms still use blueprints to communicate information — yes, 2D drawings on paper.

Being able to visualize a 3D model from 2D drawings is an important skill.

Source: Drafting Plans - Franck-Boston/iStock/Getty Images

Example 4

Solution

Let's start with the front view. Using the 2D drawing, we can see that the front face of the object is a \(4\) by \(1\) rectangle. We can draw this on the triangular dot paper.

Next, we look at the top view, which looks like a \(3\) by \(1\) rectangle. We know that this shares an edge with the front face, so we draw it on the triangular dot paper with this in mind.

Finally, the side view is a \(4\) by \(3\) rectangle, sharing edges with both the front and the top faces. 

Again, we can draw this in we have now drawn this 3D object on triangular dot paper and recognize it as a rectangular prism.

 

Try This Problem Revisited

Solution

Let's start by considering the three views we are given.

We know the line on the view of the top face represents a change in depth. We can add shading to this diagram to show this in another way.

Top View

We do something similar for the side view.

Side View

The front view, on the other hand, has no line, so it's a 2D composite shape.

Front View

Adding shading to each of our three views helps us to visualize and eventually draw the object.

We now want to go ahead and draw the 3D object. Let's start with the front view. Because there are no changes in depth, we draw this shape on triangular dot paper as a two dimensional polygon. 

Now we can look at the top view. The top view tells us that the object is two centimeters wide. When we combine this with the information from the front view, we know that the object has a change in depth and that the right portion of the top view is lower. 

At this point, the drawing is almost complete. We can use the side view to draw in the remaining sides and confirm its change in depth. 

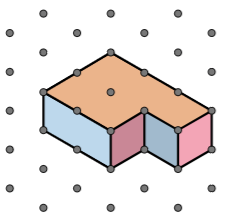
We now have a drawing of the 3D object on triangular dot paper.

Check Your Understanding 5

Question

Use the top, front, and side views to draw the 3D object on the triangular dot paper.

Answer

Check that the image you drew is the same size and shape as the answer shown. Your drawing might be rotated or in a different location on the grid.

Created with GeoGebra. Author: University of Waterloo. CC BY-NC-SA 4.0. https://ggbm.at/BzYFcQ3N

Online Version

https://ggbm.at/BzYFcQ3N

Take It With You

A designer provides the following top, front, and side views of a 3D object.

It costs \($1.25\) per square centimetre to paint the surface of this object. 

How much should the designer budget to spend on the cost of painting?