Alternative Format

Try This

Three Intersecting Lines

We know that two intersecting lines always form exactly four angles. But how many angles can we form using three lines?

Take a moment to think about this question. 

To answer it, you might try drawing three lines in different ways. There are essentially four different ways that three lines can behave.

If we think about all three lines intersecting, then you can show them all intersecting at a single point or each pair of lines intersecting at a different point. Note the pairs of opposite and supplementary angles in these diagrams.

Now it's also possible for at least two of these three lines to be parallel. If all three lines are parallel, then we only have straight angles, so really there are not many angles in this diagram that we can work with.

But if exactly two lines are parallel, then we see opposite and supplementary angles again, plus some other angles that seem to have some relationships.

Lesson Goals

• Explore angles formed by intersections of \(3\) lines.
• Explore the properties of angles formed by parallel lines and transversals.
• Define corresponding, alternate, and co-interior angles.
• Solve for unknown angles in a diagram using angle properties.

Try This!

Consider the following diagram where two parallel lines are cut by a third line.

Identify all angles that are equal in measure.

Think about this problem, then move on to the next part of the lesson.

Parallel Lines

Recall that parallel lines are lines which extend in the same direction and remain the same distance apart. Parallel lines never intersect. For example, the lines \(\overleftrightarrow{AB}\) and \(\overleftrightarrow{CD}\) are parallel lines, and we say that \(\overleftrightarrow{AB}\) is parallel to \(\overleftrightarrow{CD}\).

\(\overleftrightarrow{AB}\) and \(\overleftrightarrow{CD}\) are parallel

In geometry, we indicate that two or more lines are parallel by using an equal number of arrowheads on each line. 

The two lines \(\overleftrightarrow{RS}\) and \(\overleftrightarrow{PQ}\), however, are not parallel, because when extended they do not remain the same distance apart and will eventually intersect.

\(\overleftrightarrow{RS}\) and \(\overleftrightarrow{PQ}\) are not parallel

What Is a Transversal?

Consider the following two parallel lines, \(\overleftrightarrow{AB}\) and \(\overleftrightarrow{CD}\). If a third line, \(\overleftrightarrow{EF}\), is drawn so that it is not parallel, then it must intersect both \(\overleftrightarrow{AB}\) and \(\overleftrightarrow{CD}\), and eight angles are formed. 

In our diagram, the line \(\overleftrightarrow{EF}\) is called a transversal.

Now, in the Try This problem, you looked at a diagram that's very similar to the one on screen now, and you tried to find equal angles among the angles formed when two parallel lines are cut by a transversal.

Which angles look like they could be equal in measure? Can you determine a relationship between any angles in this diagram? Use the following investigation to explore this diagram further, and try to determine relationships between various angles.

Explore This 1

Description

Can you determine a relationship between any angles in the diagram?

Created with GeoGebra. Author: University of Waterloo. CC BY-NC-SA 4.0. https://ggbm.at/suN9FDvK

Online Version

https://ggbm.at/suN9FDvK

Explore This Summary

Now that you have had the opportunity to explore, let's take a look at the angles formed when two parallel lines are cut by a transversal. I have labelled the angles using the letters \(a\) through \(h\).

Notice that we already know that some pairs of angles are equal, because they are opposite to each other at a point where two lines intersect. This diagram contains four pairs of opposite angles:

Opposite Angles

• \(a\) and \(c\)
• \(b\) and \(d\)
• \(e\) and \(g\)
• \(f\) and \(h\)

You will also see pairs of angles that form straight lines, which are supplementary angles. You should be able to see a total of 8 pairs of supplementary angles. \(a\) and \(b\), \(a\) and \(d\), \(b\) and \(c\), as well as \(c\) and \(d\) are supplementary angles surrounding the top intersection point. 

There are four similar pairings surrounding the bottom intersection.

Supplementary Angles

• \(a\) and \(b\)
• \(a\) and \(d\)
• \(b\) and \(c\)
• \(c\) and \(d\)
• \(e\) and \(f\)
• \(e\) and \(h\)
• \(f\) and \(g\)
• \(g\) and \(h\)

In the following, Check Your Understanding. Practise identifying opposite and supplementary angles in this diagram.

Check Your Understanding 1

Question

What is the value of \(\angle FYD\) and how do you know?

Answer

\(\angle FYD = 108^\circ\), since \(\angle FYD\) is supplementary to \(\angle CYF\).

Feedback

Since \(\angle FYD\) is supplementary to \(\angle CYF\), and since supplementary angles add to \(180^\circ\), we know that \(\angle FYD = 108^\circ\).

Other Relationships

Let's take yet another look at the diagram where two parallel lines are cut by a transversal.

If you are given one angle, let's say that you know angle C is equal to 160 degrees.

You can solve for angles \(a\), \(b\), and \(d\), because they are either opposite or supplementary to angle \(c\). But can you determine the measure of the other four angles in the diagram?

Looking at these remaining unknown angles, you might suspect that there is a relationship between them and the angles that we have solved for. You could even measure them and find out that there is in fact a very apparent relationship. 

Can we use angle properties to confirm that any two pairs of angles in this diagram are either

• equal, or 
• supplementary?

Our current understanding of straight right and opposite angles is not enough for us to be able to answer this question. As a result, we're going to need to look for some other angle patterns within this diagram.

Corresponding Angles

In this diagram, \(\triangle ABC\) and \(\triangle DEF\) are congruent.

Recall that when we studied congruent triangles, we called angles that were in the same position of each triangle corresponding. So \(\angle A\) and \(\angle D\) were considered corresponding angles.

Keeping with this idea, when two parallel lines are cut by a transversal, corresponding angles are pairs of angles that are in similar positions.

Now, when we say similar positions, we mean angles that are on the same side of the transversal and on the same side of their respective parallel lines.

There are four pairs of corresponding angles in total.

Corresponding Angles

• \(a\) and \(e\)
• \(b\) and \(f\)
• \(c\) and \(g\)
• \(d\) and \(h\)

Now, to help us remember, sometimes corresponding angles are nicknamed F angles because of the F-like shape formed by the intersecting lines and transversal. 

Note that depending on the location of the corresponding angles, the F shape might be reflected or rotated. Explore corresponding angles further in the following investigation.

Explore This 2

Description

Identify a pair of corresponding angles in the diagram.

Recall that corresponding angles are nicknamed F angles because the intersecting lines and transversal form an F-like shape.

For example, \(\angle BXY\) and \(\angle DYE\) are corresponding. 

Created with GeoGebra. Author: University of Waterloo. CC BY-NC-SA 4.0. https://ggbm.at/CkvxSCdx

Online Version

https://ggbm.at/CkvxSCdx

Important Fact

Did you notice that when two parallel lines are cut by a transversal, we essentially have two identical pictures?

The top part of the diagram and the bottom part of the diagram are copies of each other, and the result is that the angles in similar positions are equal.

Example 1

Solution

We want to find the measure of \(\angle XYD\) using angle properties. So let's highlight this angle so that we remember what we are working towards.

 

We first know that \(\angle AXE\) and \(\angle XYD\) are not corresponding, nor opposite, nor do they form a straight line. This tells us that we will likely have to find an intermediate angle as a stepping stone to finding \(\angle XYD\).

We notice that \(\angle AXE\) and \(\angle CYX\) are corresponding angles. We often say that \(\angle CYX\) corresponds to \(\angle AXE\). We know that \(\angle CYX\) is equal to \(155^\circ\) since it corresponds to \(\angle AXE\), and we know that corresponding angles are equal.

Next, notice that \(\angle CYX\) and \(\angle XYD \) are supplementary angles. Thus, \(\angle XYD \) is equal to \(25^\circ\) since it is supplementary to \(\angle CYX\), and we know that supplementary angles must add to \(180^\circ\). 

In summary, we have the following:

• \(\angle CYX = 155^\circ\) (corresponds to \(\angle AXE\))
• \(\angle XYD = 25^\circ\) (supplementary to \(\angle CYX\))

In conclusion, \(\angle XYD = 25^\circ\).

Check Your Understanding 2

Question

What is the value of \(\angle BXE\)? Explain how you know.

Answer

\(\angle BXE = 78^\circ\), since \(\angle BXE\) is supplementary to \(\angle YXB\).

Feedback

Since \(\angle BXE\) is supplementary to \(\angle YXB\), and since supplementary angles add to \(180^\circ\), we know that \(\angle BXE = 78^\circ\).

Finding Equal Angles

Consider the following two parallel lines, \(\overleftrightarrow{AB}\) and \(\overleftrightarrow{CD}\), that intersect the transversal \(\overleftrightarrow{EF}\) at \(X\) and \(Y\), respectively, such that \(\angle XYD\) is equal to \(45^\circ\).

Since \(\angle EXB\) corresponds to \(\angle XYD\) and since corresponding angles are equal, we know that \(\angle EXB\) is equal to \(45\) degrees, as well.

What other angles are equal to \(45^\circ\) in this diagram, and how do you know? 

Well, we can see that \(\angle AXY\) is opposite to \(\angle EXB\). And since opposite angles are equal, \(\angle AXY\) is equal to \(45^\circ\).

Similarly, \(\angle CYF\) and \(\angle XYD\) are opposite angles. So \(\angle CYF\) is also equal to \(45^\circ\).

In this diagram, we see opposite angles, and we see corresponding angles.

But we also see another pair of angles that are equal, namely \(\angle AXY\) and \(\angle XYD\). These two angles are not opposite, nor are they corresponding. So we have to come up with another name to describe the relationship.

Alternate Angles

A pair of angles that are formed between the pair of parallel lines on opposite sides of the transversal are called alternate angles.

In this diagram, angles \(c\) and \(e\) are alternate angles, as are angles \(d\) and \(f\).

Alternate Angles

• \(c\) and \(e\)
• \(d\) and \(f\)

To help us remember, sometimes alternate angles are nicknamed Z angles, because of the Z-like shape formed by the intersecting lines in transversal. 

Note that depending on the location of the alternate angles, the Z shape might be reflected.

Important Fact

So let's jump back to our diagram of two parallel lines in a transversal again. We showed that if \(\angle XYD\) is equal to \(45^\circ\), then the alternate angle, \(\angle AXY\), is also equal to \(45 ^\circ\).

If instead \(\angle XYD\) is equal to \(90^\circ\), then through similar steps, we can show that \(\angle EXB\) is equal to \(90^\circ\), because it corresponds to \(\angle XYD\).

And then that \(\angle AXY\) is equal to \(90^\circ\), because it is opposite \(\angle EXB\). Again, we have two alternate angles, \(\angle AXY\) and \(\angle XYD\), that are equal.

 

As a third and final example, if \(\angle XYD\) is equal to \(110^\circ\), we can show that \(\angle EXB\) is equal to \(110^\circ\), because it corresponds to \(\angle XYD\). 

And then go ahead and show that \(\angle AXY\) is equal to \(110^\circ\), because it is opposite \(\angle EXB\). Again, the two alternate angles, \(\angle AXY\) and \(\angle XYD\), are equal.

You should be able to convince yourself that no matter what the measure of \(\angle XYD\), its alternate angle, \(\angle AXY\), will always be equal in measure. It turns out that this is true for any pair of alternate angles.

Check Your Understanding 3

Question

What is the value of \(\angle AXY\)? Explain how you know.

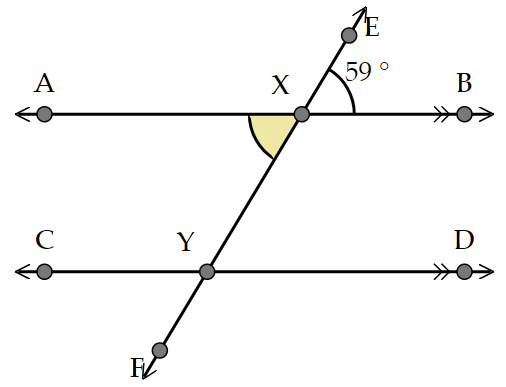
Answer

\(\angle AXY = 59^\circ\), since \(\angle AXY\) is opposite to \(\angle BXE\).

Feedback

Since \(\angle AXY\) is opposite to \(\angle BXE\), and since opposite angles are equal, we know that \(\angle AXY = 59^\circ\).

Recognizing More Supplementary Angles

So far, we have found all angles in the following diagram that are equal to \(110^\circ\).

But what do we know about the angles that are left? Well, using our knowledge of straight angles, we can determine that \(\angle BXY\) is equal to \(70^\circ\), because it is supplementary to \(\angle AXY\). Notice that there is now a pair of angles that are located between the parallel lines on the same side of the transversal. We call this pair of angles co-interior angles.

We call this pair of angles co-interior angles. 

Co-Interior Angles

Recall our diagram:

Notice angle \(c\) and \(f\) are co-interior angles, as are angles \(d\) and \(e\).

To help us remember, sometimes co-interior angles are nicknamed C angles, because of the C shape formed by the intersecting lines and the transversal.

Co-Interior Angles

• \(c\) and \(f\)
• \(d\) and \(e\)

Now depending on the location of the co-interior angles, the C shape might be reflected.

Example 2

Solution

Now, there are many ways to find the measures of the unknown angles, and we're going to follow just one of these paths in the solution. 

First, we might notice that the lines forming \(\angle XYD\) and \(\angle EXB\) make an F shape, and so these angles are corresponding angles. We know that \(\angle EXB\) is equal to \(112^\circ\) since it corresponds to \(\angle XYD\), and we know the corresponding angles are equal.

Next, the lines forming angle bxy and \(\angle XYD\) make a C shape. And so these angles are co-interior angles. We know that \(\angle BXY\) is equal to \(68^\circ\) since it is co-interior to \(\angle XYD\), and we know co-interior angles to be supplementary.

The lines forming \(\angle AXY\) and \(\angle XYD\) make a Z shape. And so these angles are alternate angles. Thus, we know that \(\angle AXY\) is equal to \(112^\circ\)  since it is alternate to \(\angle XYD\), and we know alternate angles to be equal.

Finally, we can find \(\angle AXE\) by recognizing that it is opposite to \(\angle BXY\). We know that \(\angle AXE\) is equal to \(68^\circ\) since it is opposite \(\angle BXY\), and we know opposite angles to be equal.

In summary, we have the following:

• \(\angle EXB = 112^\circ\) (corresponds to \(\angle XYD\))
• \(\angle BXY=68^\circ\) (co-interior to \(\angle XYD\))
• \(\angle AXY = 112^\circ\) (alternate to \(\angle XYD\))
• \(\angle AXE=68^\circ\) (opposite to \(\angle BXY\))

Summary

We have explored some new relationships between a pair of angles formed by two parallel lines and a transversal.

Remember that these patterns also have nicknames, the F, Z, and C patterns, respectively, which come from the shape formed by the intersecting lines in the transversal. But make sure not to forget about the properties of opposite, complementary, and supplementary angles from before, because they're also helpful when solving problems involving angles.

Check Your Understanding 4

Question

What is the value of \(\angle BXE\)? Explain how you know.

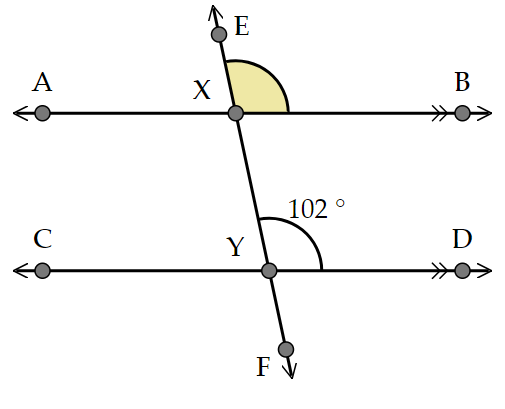
Answer

\(\angle BXE = 102^\circ\), since \(\angle BXE\) is corresponding to \(\angle DYX\).

Feedback

Since \(\angle BXE\) corresponds to \(\angle DYX\), and since corresponding angles are equal, we know that \(\angle BXE = 102^\circ\). 

Example 3

Solution

When solving geometry problems, sometimes it is helpful to construct a line to help us find the solution. This is the case in the following diagram. Let's draw a line parallel to \(\overleftrightarrow{AB}\) through the point \(C\) and call it \(\overleftrightarrow{XY}\).

Note that the obtuse angle \(\angle BCD\) is now the sum of the two angles \(\angle BCY\) and \(\angle YCD\). When we consider the two parallel lines, \(\overleftrightarrow{AB}\) and \(\overleftrightarrow{XY}\), the line segment \(\overline{BC}\) is a transversal. Note that you can extend the segment past \(C\) and \(B\) if it's helpful to do so.

Notice that \(\angle ABC\) and \(\angle BCY\) are alternate angles. Since alternate angles are equal, \(\angle BCY\) is equal to \(30^\circ\).

When we consider the two parallel lines, \(\overleftrightarrow{XY}\) and \(\overleftrightarrow{DE}\), the line segment \(\overline{CD}\) is a transversal. And again, you can extend the line segment past its endpoints if you find it helpful.

Notice that \(\angle YCD\) and \(\angle CDE\) are co-interior angles.

Since co-interior angles are supplementary, \(\angle YCD\) is equal to \(100^\circ\).

We now have the information we need to determine the measure of the obtuse angle \(\angle BCD\), which is the sum of \(\angle BCY\) and \(\angle YCD\). 

\(\angle BCD = 30^\circ + 100 ^\circ \class{timed in7}{ = 130^\circ}\)

Check Your Understanding 5

Question

What is the measure of the obtuse angle \(\angle ECD\)?

Answer

\(\angle ECD = 63^\circ\)

Feedback

\(\angle ABC\) and \(\angle BCD\) are alternate angles.

\(\angle BCD = 63^\circ\)

\(\angle BCD\) and \(\angle EDC\) are supplementary angles.

\(\begin{align*} \angle EDC + 63^\circ & = 180^\circ \\ \angle EDC & = 117^\circ\end{align*}\)

Therefore, \(\angle EDC = 117^\circ\).

Example 4

An interesting application of the angle properties that we have learned about in this lesson is that we can use a transversal to show that two lines are parallel. 

Solution

In this lesson, we learned that if two lines ab and cd are parallel, then one result is that corresponding angles must be equal. With this in mind, it is tempting to look at the diagram that we're given and see that two corresponding angles measuring \(53^\circ\) means that the two lines \(\overleftrightarrow{AB}\) and \(\overleftrightarrow{CD}\) must be parallel.

But mathematically, it's not okay to use our fact in the opposite direction without knowing that it's possible to do so. To be sure that lines \(\overleftrightarrow{AB}\) and \(\overleftrightarrow{CD}\) are parallel, we're going to have to do a bit more work. We need to use what we know about angles and intersecting lines to convince ourselves without a doubt that from the information given, the two lines ab and cd must be parallel.

We're going to start by assuming that \(\overleftrightarrow{AB}\) and \(\overleftrightarrow{CD}\) are not parallel.

When two lines are not parallel, we know that they must intersect at a point. We are going to call this point \(Z\). To help us visualize this, I'm going to redraw our diagram and accentuate our assumption that the lines are not parallel and show them meeting at a point \(Z\).

Notice that when the lines \(\overleftrightarrow{AB}\) and \(\overleftrightarrow{CD}\) are not parallel, then together with the line \(\overleftrightarrow{EF}\), they form a triangle, of which we are given one angle, \(\angle XYZ\). 

But since we know that \(\angle EXZ\) is equal to \(53^\circ\), we know that \(\angle ZXY\) is equal to \(127\) degrees, because it is supplementary to \(\angle FXZ\).

Next, we know the angles in a triangle must have a sum of \(180^\circ\). 

\(\begin{align*} \angle XZY + 127^\circ +53^\circ & = 180^\circ \\ \class{timed in7}{\angle XZY} &\; \class{timed in7}{ = 0^\circ} \end{align*}\)

So what does this mean? If two lines are not parallel, then we have a triangle that must have an angle equal to \(0^\circ\). But to form a triangle, all three angles must be greater than \(0^\circ\).

The only way to avoid this problem is if this triangle doesn't actually exist. That is, the lines \(\overleftrightarrow{AB}\) and \(\overleftrightarrow{CD}\) never actually meet. 

The result is that \(\overleftrightarrow{AB}\) and \(\overleftrightarrow{CD}\) must be parallel.

What we've done is that we have shown if \(\angle EXB\) equals \(53^\circ\) and \(\angle XYD\) equals \(53^\circ\), then the two lines \(\overleftrightarrow{AB}\) and \(\overleftrightarrow{CD}\) must be parallel.

Take It With You

Consider \(\triangle ABC\). A line, parallel to \(\overleftrightarrow{BC}\), is drawn through the vertex \(A\).

How can you use this diagram to show that the sum of the interior angles of a triangle is equal to \(180^\circ\)?

That is, how can you be sure that 

\(x + y + z = 180^\circ\)