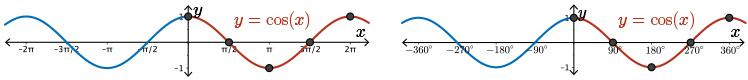For \(y=\sin(x)\), we identified five key points in one period starting on the \(y\)-axis.
In radian measure, these points are \((0,0), \left( \dfrac{\pi}{2} , 1 \right) , (\pi, 0), \left( \dfrac{3\pi}{2} , -1 \right)\), and \((2\pi , 0)\).
In degrees, the five key points are \((0,0), (90^{\circ} , 1), (180^{\circ} , 0), (270^{\circ} , -1)\), and \((360^{\circ} , 0)\).
Once a five-point sketch is complete, we can sketch as many periods as we require.

For \(y = \cos(x)\), we identified five key points in one period starting on the \(y\)-axis.
In radian measure, these points are \((0,1), \left( \dfrac{\pi}{2} , 0 \right) , (\pi , -1) , \left( \dfrac{3\pi}{2} , 0 \right)\), and \((2\pi , 1)\).
In degrees, the five key points are \((0,1) , (90^{\circ} , 0) , (180^{\circ} , -1) , (270^{\circ} , 0)\), and \((360^{\circ} , 1)\).
Once the five point sketch is complete, we can sketch as many periods as we require.