Through earlier studies in mathematics, a variety of functions have been used to model specific applications.

The relationship between a worker's pay and the number of hours worked could be modelled with a simple linear function.

When a ball is thrown into the air, its height above the ground over time can be modelled using a quadratic function.

Growth and decay situations can be modelled with exponential functions.

In this module, sine and cosine functions will be used to model various physical situations that are periodic.

The pendulum of an antique clock makes \(30\) complete swings in one minute. A complete swing moves the pendulum from the extreme right point, \(R\), to the extreme left point, \(L\), and back to \(R\) again. The horizontal distance between the two extreme points \(R\) and \(L\) is \(36\) cm.

a. Determine the period and amplitude of this motion.

Solution

Since there are \(30\) complete swings in \(60\) seconds (\(1\) minute), \(1\) period is \(60 \div 30 = 2\) seconds.

The horizontal distance between the two extreme points is \(36\) cm.

That is, the maximum minus the minimum is \(36\).

The amplitude is half of this value so the amplitude is \(18\).

The pendulum of an antique clock makes \(30\) complete swings in one minute. A complete swing moves the pendulum from the extreme right point, \(R\), to the extreme left point, \(L\), and back to \(R\) again. The horizontal distance between the two extreme points \(R\) and \(L\) is \(36\) cm.

b. Draw a sketch to model the pendulum swing for the first \(6\) seconds. Assume the pendulum starts at \(R\).

Solution

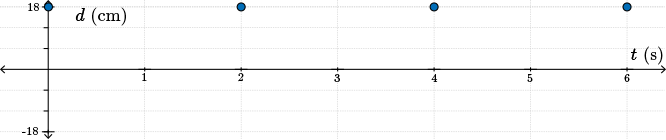
Let \(d\) represent the horizontal distance from \(\color{Mulberry}M\), with positive distance to the right and negative distance to the left.

When the pendulum is at \(\color{NavyBlue}R\), \(d=18\). When the pendulum is at \(\color{BrickRed}L\), \(d=-18\).

Since the period is \(2\) seconds, the pendulum will be at \(\color{NavyBlue}R\), a maximum, at \(0\), \(2\), \(4\), and \(6\) seconds.

The minimum will occur at the halfway point of each period so the pendulum will be at \(\color{BrickRed} L\) at \(1\), \(3\), and \(5\) seconds.

And halfway between the maximum and minimum, the pendulum will be at \(\color{Mulberry}M\).

The pendulum will be at \(\color{Mulberry}M\) at \(0.5\), \(1.5\), \(2.5\), \(3.5\), \(4.5\), and \(5.5\) seconds.

A sketch is shown.

The pendulum of an antique clock makes \(30\) complete swings in one minute. A complete swing moves the pendulum from the extreme right point, \(R\), to the extreme left point, \(L\), and back to \(R\) again. The horizontal distance between the two extreme points \(R\) and \(L\) is \(36\) cm.

c. Determine an equation to model the path of the pendulum.

Solution

By referring to the sketch, it would appear that the path of the pendulum can be modelled using a cosine function,

Since a maximum point on the sketch is on the \(y\)-axis (or in this case, the \(d\)-axis), there is no horizontal translation and so \(h=0\).

The central horizontal axis is on the \(x\)-axis (or in this case, the \(t\)-axis) so there is no vertical translation and \(k=0\).

The amplitude is \(18\) cm. Since a maximum point is on the positive \(y\)-axis, there has been no reflection about the \(x\)-axis and \(a=18\).

The pendulum of an antique clock makes \(30\) complete swings in one minute. A complete swing moves the pendulum from the extreme right point, \(R\), to the extreme left point, \(L\), and back to \(R\) again. The horizontal distance between the two extreme points \(R\) and \(L\) is \(36\) cm.

c. Determine an equation to model the path of the pendulum.

Solution

The period is \(2\) seconds. Thus, \(b = \dfrac{2\pi}{\text{period}} = \dfrac{2\pi}{2} = \pi\).

Substituting for \(a=18\), \(b=\pi\), \(h=0\), and \(k=0\) into \(d=a\cos[b(x-h)]+k\), we obtain \(d=18\cos(\pi x)\).

If we use \(t\) instead of \(x\), an equation of the function graphed becomes \(d=18\cos(\pi t)\), \(0\leq t \leq 6\).

• When \(d \lt 0\), the pendulum is closer to \(\color{BrickRed}L\) than it is to \(\color{NavyBlue}R\).
• When \(d \gt 0\), the pendulum is closer to \(\color{NavyBlue}R\) than it is to \(\color{BrickRed}L\).
• When \(d=0\), the pendulum is at \(\color{Mulberry}M\).

The pendulum of an antique clock makes \(30\) complete swings in one minute. A complete swing moves the pendulum from the extreme right point, \(R\), to the extreme left point, \(L\), and back to \(R\) again. The horizontal distance between the two extreme points \(R\) and \(L\) is \(36\) cm.

d. Using the model, determine the position of the pendulum at \(4.75\) seconds.

Solution

Substitute \(t=4.75\) into \(d=18\cos(\pi t)\):

At \(t=4.75\), the pendulum is located \(9\sqrt{2}\) cm to the left of the middle position, closer to \(L\) than to \(R\).

The pendulum of an antique clock makes \(30\) complete swings in one minute. A complete swing moves the pendulum from the extreme right point, \(R\), to the extreme left point, \(L\), and back to \(R\) again. The horizontal distance between the two extreme points \(R\) and \(L\) is \(36\) cm.

d. Using the model, determine the position of the pendulum at \(4.75\) seconds.

Solution

At \(t=4.75\), the pendulum is located \(9\sqrt{2}\) cm to the left of the middle position, closer to \(L\) than to \(R\).

We can use the sketch to see that our calculation is reliable.

This is a good time to note that the motion of the pendulum is only approximately sinusoidal. The exact motion of the pendulum would be studied in university physics or applied mathematics courses.

The pendulum of an antique clock makes \(30\) complete swings in one minute. A complete swing moves the pendulum from the extreme right point, \(R\), to the extreme left point, \(L\), and back to \(R\) again. The horizontal distance between the two extreme points \(R\) and \(L\) is \(36\) cm.

e. At what times during the first \(6\) seconds will the pendulum be horizontally \(9\) cm to the right of its position at \(M\)?

Solution

Substitute \(9\) for \(d\) into \(d=18\cos(\pi t)\):

Let \(\theta=\pi t\). We want \(\cos(\theta)=\frac{1}{2}\). The reference angle is \(\frac{\pi}{3}\).

Since \(\cos(\theta)\gt 0\), \(\theta\) is in quadrant 1 or in quadrant 4.

In quadrant 1, \(\theta = \frac{\pi}{3}\) and in quadrant 4, \(\theta=2\pi - \frac{\pi}{3} = \frac{5\pi}{3}\), for \(0\leq\theta\leq 2\pi\).

Since \(\theta = \pi t\),

These two possibilities for \(t\) lie in the interval \(0 \leq t \leq 2\).

To get all times such that \(0\leq t \leq 6\), add multiples of the period length. It follows that the pendulum will be horizontally \(9\) cm to the right of its position at \(M\) for \(t=\frac{1}{3}, 1\frac{2}{3}, 2\frac{1}{3}, 3\frac{2}{3},4\frac{1}{3},5\frac{2}{3}\) seconds.