Sketch the graph of \(y = \cot(x)\), \( 0 \leq x \leq 2\pi\) from its reciprocal function \(y = \tan(x)\).

1. Since \(\tan(x) = 1\) when \(x = \dfrac{\pi}{4}\) and \(x = \dfrac{5\pi}{4}\), \(\cot(x) = 1\) when \(x = \dfrac{\pi}{4}\) and \(x = \dfrac{5\pi}{4}\). Since \(\tan(x) = -1\) when \(x = \dfrac{3\pi}{4}\) and \(x = \dfrac{7 \pi}{4}\), \(\cot(x) = -1\) when \(x = \dfrac{3\pi}{4}\) and \(x = \dfrac{7\pi}{4}\). The four points \(\left( \dfrac{\pi}{4} , 1 \right)\), \(\left( \dfrac{3\pi}{4} , -1 \right)\), \(\left( \dfrac{5\pi}{4} , 1 \right)\), and \(\left( \dfrac{7\pi}{4} , -1 \right)\) are on both \(y = \tan(x)\) and \(y = \cot(x)\).

2. The \(x\)-intercepts of \(y = \tan(x)\) occur when \(x = 0, x = \pi\), and \(x = 2\pi\). The cotangent function will therefore have vertical asymptotes for these values of \(x\).

Sketch the graph of \(y = \cot(x)\), \( 0 \leq x \leq 2\pi\) from its reciprocal function \(y = \tan(x)\).

3. The asymptotes of \(y = \tan(x) = \dfrac{\sin(x)}{\cos(x)}\) occur when \(x = \dfrac{\pi}{2}\) and \(x = \dfrac{3\pi}{2}\) since the denominator \(\cos(x)\) equals \(0\) for these values of \(x\). At these same values of \(x\), the numerator \(\sin(x)\) is either \(1\) or \(-1\). In the reciprocal \(y = \cot(x) = \dfrac{\cos(x)}{\sin(x)}\), for the same values of \(x\), the numerator \(\cos(x)\) equals \(0\) and the denominator \(\sin(x)\) is either \(1\) or \(-1\). In either case, the value of \(y = \cot(x)\) is \(0\). Therefore, the \(x\)-intercepts of \(y = \cot(x)\) occur when \(x = \dfrac{\pi}{2}\) and \(x = \dfrac{3\pi}{2}\).

The final graph is shown for you.

4. The argument for the behaviour around the asymptotes is similar to the argument around the asymptotes for \(y = \csc(x)\) and \(y = \sec(x)\), and will not be repeated here.

Properties of \(y = \cot(x)\)

For the cotangent function, state the \(x\) and \(y\)-intercepts, the period and the equations for any asymptotes, and the domain and range.

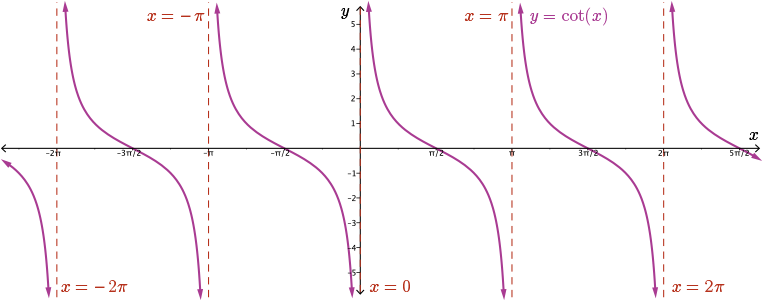
The \(x\)-intercepts are \(x = \pm \frac{3\pi}{2}, x = \pm \frac{\pi}{2}, \text{ and } x=\frac{5\pi}{2}\). In general, the \(x\)-intercepts are \(x = \frac{\pi}{2} + n\pi\), \(n \in \mathbb{Z}\).

There is no \(y\)-intercept. The period of \(y = \cot(x)\) is \(\pi\). There are no horizontal asymptotes. The vertical asymptotes occur every \(\pi\) units with one of them at \(x = 0\). Therefore, the equations of the vertical asymptotes can be written \(x = n\pi, n \in \mathbb{Z}\). The domain is \(\left\{ x \mid x \neq n\pi, x \in \mathbb{R}, n \in \mathbb{Z} \right\}\). The range is \(\left\{ y \mid y \in \mathbb{R} \right\}\).

Summary

In this module, we have sketched the three functions: \(y = \csc(x), y = \sec(x),\) and \(y = \cot(x)\).

We have also looked at properties of each.

In upcoming modules, we will look at transformations of \(y = \sin(x)\) and \(y = \cos(x)\).