2. Trigonometric Functions
  3. Transformations of the Sine and Cosine Functions

Partial Solutions


  1. There is no solution provided for this question.
    1. From the equation \( y = -2\sin{ \left[ \tfrac{1}{3} (x - 30^\circ) \right] } + 4 \), we can determine the characteristics of its graph:
      • amplitude: \( a = -2 \), corresponding to an amplitude of \( 2 \) and a reflection about the \( x \)-axis
      • period: \( b = \tfrac{1}{3} \implies \dfrac{360^\circ}{\tfrac{1}{3}} = 1080^\circ \)
      • phase shift: \( h = 30^\circ \) which corresponds to a translation right \( 30^\circ \)
      • vertical displacement: \( k = 4 \), corresponding to a translation up \( 4 \) units

      Using the vertical displacement, we determine the central horizontal axis to be \( y = 4 \). Using the amplitude, we determine the maximum value of \( y \) to be \( 4 + 2 = 6 \) and the minimum value to be \( 4 - 2 = 2 \).

      The point \( (0, 0) \) marks the beginning of the first period of the base graph, \( y = \sin(x) \), to the right of the \( y \)-axis. The image of this point under the transformation is \( \left( 30^\circ, 4 \right) \). Since this point lies on the central horizontal axis, two other points on the transformed graph will occur a half period and a full period to the right of this point, at points \( (570^\circ, 4) \) and \( (1110^\circ, 4) \).

      Combining this with the phase shift and the period, we obtain the following sketch:

      Five point graph of sin passing through labelled points (30,4),(570,4),(1110,4)

      Using the sketch, we see that the first minimum to the right of the \( y \)-axis occurs at

      \[\begin{align*} x &= 30^\circ + \tfrac{1}{4}\text{(period)} \\ x &= 30^\circ + 270^\circ \\ x &= 300^\circ \end{align*}\]

      which corresponds to the point \( (300^\circ, 2) \).

      Half a period after the first minimum will be where the first maximum occurs; that is, at

      \[\begin{align*} x &= 300^\circ + \tfrac{1}{2}\text{(period)} \\ x &= 300^\circ + 540^\circ \\ x &= 840^\circ \end{align*}\]

      which corresponds to the point \( (840^\circ, 6) \).

      A full sketch of the graph is given below:

      Five point graph of sin passing through (30, 4),(300,2),(570,4),(840,6),(1110,4)
    2. From the equation \( y = 5\cos{ \left( 3x + \tfrac{\pi}{2} \right) } - 4 = 5\cos{\left[ 3 \left( x + \tfrac{\pi}{6} \right) \right]} - 4 \), we can determine the characteristics of its graph:
      • amplitude: \( a = 5 \), corresponding to an amplitude of \( 5 \)
      • period: \( b = 3 \implies \dfrac{2\pi}{3} \)
      • phase shift: \( h = -\tfrac{\pi}{6} \) which corresponds to a translation left \( \tfrac{\pi}{6} \) units
      • vertical displacement: \( k = -4 \)

      Using the vertical displacement, we determine the central horizontal axis to be \( y = -4 \). Using the amplitude, we determine the maximum value of \( y \) to be \( -4 + 5 = 1 \), and the minimum value to be \( -4 - 5 = -9 \).

      The point \( (0, 1) \) marks the beginning of the first period of the base graph, \( y = \cos(x) \), to the right of the \( y \)-axis. The image of this point under the transformation is \( \left( -\tfrac{\pi}{6}, 1 \right) \). Since this was a maximum on the base graph, and the transformed graph is not vertically reflected, it is also a maximum on the transformed graph. Then, the second maximum will occur a full period to the right of this point, at

      \[ \left( -\tfrac{\pi}{6} + \tfrac{2\pi}{3}, 1 \right) = \left( \tfrac{\pi}{2}, 1 \right) \]

      The minimum point of the transformed graph then occurs halfway between the two maximums, at

      \[ \left( \dfrac{-\tfrac{\pi}{6} + \tfrac{\pi}{2}}{2}, -9 \right) = \left( \dfrac{-\tfrac{\pi}{6} + \tfrac{3\pi}{6}}{2}, -9 \right) = \left( \dfrac{\tfrac{2\pi}{6}}{2}, -9 \right) = \left( \tfrac{\pi}{6}, -9 \right) \]

      giving the following sketch:

      Graph of y=5*cos(3x + pi/2) - 4 with points described in solution labelled

      From the sketch we see that the first minimum right of the \( y \)-axis occurs at \( \left( \tfrac{\pi}{6}, -9 \right) \) and the first maximum to the right of the \( y \)-axis occurs at \( \left( \tfrac{\pi}{2}, 1 \right) \).

  3. There is no solution provided for this question.
  4. From the equation \( y = -\cos{ \left[ \tfrac{1}{3} \left( x + \tfrac{5\pi}{6} \right) \right] } - 2 \), we can determine the characteristics of its graph:
    • amplitude: \( a = -1 \) which corresponds to a reflection about the \( x \)-axis
    • period: \( b = \tfrac{1}{3} \implies \dfrac{2\pi}{\tfrac{1}{3}} = 6\pi \)
    • phase shift: \( h = -\tfrac{5\pi}{6} \) which corresponds to a translation left \( \tfrac{5\pi}{6} \) units
    • vertical displacement: \( k = -2 \)

    Using the vertical displacement, we determine the central horizontal axis to be \( y = -2 \). Using the amplitude, we determine the maximum value of \( y \) to be \( -2 + 1 = -1 \), and the minimum value to be \( -2 - 1 = -3 \).

    Since \( (0, 1) \) is a maximum point on the base graph \( y = \cos(x) \), applying the transformations tell us that a minimum point of \( y = -\cos{ \left[ \tfrac{1}{3} \left( x + \tfrac{5\pi}{6} \right) \right] } - 2 \) will occur at \( \left( -\tfrac{5\pi}{6}, -3 \right) \) and another minimum point occurs one period later, at \( \left( -\tfrac{5\pi}{6} + 6\pi, -3 \right) = \left( \tfrac{31\pi}{6}, -3 \right) \).

    A maximum point occurs when

    \[\begin{align*} x &= -\tfrac{5\pi}{6} + \tfrac{1}{2}\text{(period)} \\ x &= -\tfrac{5\pi}{6} + 3\pi \\ x &= \tfrac{13\pi}{6} \end{align*}\]

    which corresponds to the point \( \left(\tfrac{13\pi}{6}, -1\right) \).

    The points which lie on the horizontal axis occur a \( \tfrac{1}{4} \) period and \( \tfrac{3}{4} \) period to the right of the leftmost endpoint:

    \[\begin{align*} x &= -\tfrac{5\pi}{6} + \tfrac{1}{4}(\text{period}) \\ x &= -\tfrac{5\pi}{6} + \tfrac{1}{4}(6\pi) \\ x &= -\tfrac{5\pi}{6} + \tfrac{3}{2}\pi \\ x &= -\tfrac{5\pi}{6} + \tfrac{9\pi}{6} \\ x &= \tfrac{4\pi}{6} \\ x &= \tfrac{2\pi}{3} \\ \end{align*}\]which corresponds to the point \( \left( \tfrac{2\pi}{3}, -2 \right) \).
    \[\begin{align*} x &= -\tfrac{5\pi}{6} + \tfrac{3}{4}(\text{period}) \\ x &= -\tfrac{5\pi}{6} + \tfrac{3}{4}(6\pi) \\ x &= -\tfrac{5\pi}{6} + \tfrac{9}{2}\pi \\ x &= -\tfrac{5\pi}{6} + \tfrac{27\pi}{6} \\ x &= \tfrac{22\pi}{6} \\ x &= \tfrac{11\pi}{3} \\ \end{align*}\]which corresponds to the point \( \left( \tfrac{11\pi}{3}, -2 \right) \).
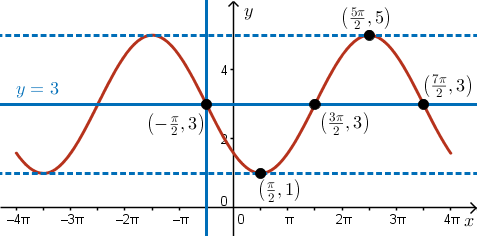
    Putting these all together, we obtain the following sketch: 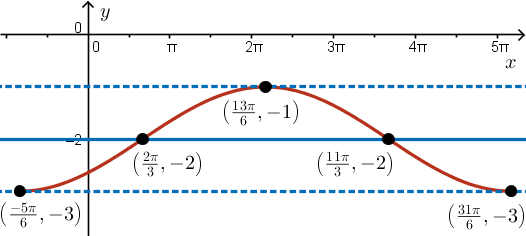Sketch of graph with characteristics described in solution
  5. There is no solution provided for this question.
  6. From the equation \( y = -2\sin{ \left( \tfrac{x}{2} + \tfrac{\pi}{4} \right) } + 3 = -2\sin{ \left[ \tfrac{1}{2} \left( x + \tfrac{\pi}{2} \right) \right] } + 3 \), we can determine the characteristics of its graph:
    • amplitude: \( a = -2 \) which corresponds to a vertical stretch by a factor of \( 2 \) and a reflection about the \( x \)-axis
    • period: \( b = \tfrac{1}{2} \) which corresponds to a period of \( \dfrac{2\pi}{\tfrac{1}{2}} = 4\pi \)
    • phase shift: \( h = -\tfrac{\pi}{2} \) which corresponds to a translation left \( \tfrac{\pi}{2} \) units
    • vertical displacement: \( k = 3 \) which corresponds to a central horizontal axis of \( y = 3 \)

    Using the amplitude and the central horizontal axis, we determine the maximum value of \( y \) to be \( 3 + 2 = 5 \), and the minimum value to be \( 3 - 2 = 1 \).

    On the base graph of \( y = \sin(x) \), \( (0, 0) \) is a point on its central horizontal axis that lies within the domain \( -4\pi \leq x \leq 4\pi \). On the transformed graph, this corresponds to the point \( \left( -\tfrac{\pi}{2}, 3 \right) \).

    A minimum point of \( y = -2\sin{ \left[ \tfrac{1}{2} \left( x + \tfrac{\pi}{2} \right) \right] } + 3 \) occurs a quarter period to the right of \( \left( -\tfrac{\pi}{2}, 3 \right) \), at \( \left( -\tfrac{\pi}{2} + \tfrac{1}{4}(4\pi), 1 \right) = \left( \tfrac{\pi}{2}, 1 \right) \).

    A maximum point of \( y = -2\sin{ \left[ \tfrac{1}{2} \left( x + \tfrac{\pi}{2} \right) \right] } + 3 \) occurs a half period to the right of the minimum point, \( \left( \tfrac{\pi}{2}, 1 \right) \), at \( \left( \tfrac{\pi}{2} + \pi, 1 + 4 \right) = \left( \tfrac{5\pi}{2}, 5 \right) \).

    Two other points on the central horizontal axis will occur a half period and a full period to the right of \( \left( -\tfrac{\pi}{2}, 3 \right) \), at

    \[ \left( -\tfrac{\pi}{2} + \tfrac{1}{2}(4\pi), 3 \right) = \left( \tfrac{3\pi}{2}, 3 \right) \] and\[ \left( -\tfrac{\pi}{2} + 4\pi, 3 \right) = \left( \tfrac{7\pi}{2}, 3 \right) \]

    Labelling these points, we obtain the full five-point sketch: Graph of y=-2*sin( x/2 + pi/4 ) + 3 as described in solution