Working with Sinusoidal Functions Alternative Format

Lesson Part 1

Recall

In an earlier module, we looked at the transformational form of two parent sinusoidal functions \(y = \sin(x)\) and \(y = \cos(x)\).

We graphed sinusoidal functions using a variety of techniques.

We discussed the features of the functions and how to determine them from the equation. The roles of \({\color{BrickRed}a}\), \({\color{NavyBlue}b}\), \(\color{Mulberry}h\), and \({\color{Violet}k}\) are listed below:

• The amplitude is \(\lvert {\color{BrickRed}a} \rvert\) and can be determined by the formula \(\dfrac{\text{maximum } - \text{ minimum}}{2}\).
  If \({\color{BrickRed}a} \lt 0\), the parent function is reflected about the \(x\)-axis.
• The period is \(\dfrac{2\pi}{\color{NavyBlue}\lvert b \rvert}\) radians or \(\dfrac{360^{\circ}}{\color{NavyBlue}\lvert b \rvert}\).
  If \({\color{NavyBlue}b} \lt 0\), the parent function is reflected about the \(y\)-axis.
• The phase shift is \(\color{Mulberry}h\).
• The vertical displacement is \({\color{Violet}k}\) and can be calculated using \(\dfrac{\text{maximum } + \text{ minimum}}{2}\).
  \(k\) is the average of the maximum and minimum values of the function.
  The equation of the central horizontal axis is \(y = {\color{Violet}k}\).
• The maximum value is \({\color{Violet}k} + {\color{BrickRed}\lvert a \rvert}\) and the minimum value is \({\color{Violet}k} - {\color{BrickRed}\lvert a \rvert}\).

Examples

In the first part of this module, we will be determining an equation from either some given information or from a graph.

Example 1

Determine an equation for a sine function that has been reflected about the \(x\)-axis, has a maximum value \(12\), a minimum value \(2\), a period \(4\pi\), and a phase shift \(-\dfrac{\pi}{3}\).

Solution

The equation is of the form

Since there is a reflection about the \(x\)-axis, \(a \lt 0\).

To determine the amplitude, we subtract the minimum value, \(2\), from the maximum value, \(12\), and divide the result by \(2\). So, the amplitude is \(\dfrac{12-2}{2} = \dfrac{10}{2} = 5\). Combining the fact that \(a\lt 0\) and the amplitude is \(5\), it follows that \(a = -5\).

We know that \(k\) is the average of the maximum and minimum values so \(k = \dfrac{12+2}{2} = \dfrac{14}{2} = 7\). (It follows that the equation of the central horizontal axis is \(y = 7\).)

Since the phase shift is given, we know that \(h = -\dfrac{\pi}{3}\).

We know that the period of a sinusoidal function \(= \dfrac{2\pi}{\lvert b \rvert}\). Rearranging, we get \(\lvert b \rvert = \dfrac{2\pi}{\text{period}} = \dfrac{2\pi}{4\pi} = \dfrac{1}{2}\).

Since there is no reflection about the \(y\)-axis, \(b \gt 0\) and it follows that \(b = \dfrac{1}{2}\). Combining the information, we have \(a = -5, b = \dfrac{1}{2}, h = -\dfrac{\pi}{3}\) and \(k = 7\). A possible equation is \(y = -5\sin\left[\dfrac{1}{2}\left(x + \dfrac{\pi}{3}\right)\right]+7\).

Notice that it's a possible equation. There are other equations, and we'll look at that as we move through this module.

Check Your Understanding A

This question is not included in the Alternative Format, but can be accessed in the Review section of the side navigation.

Lesson Part 2

Examples

Example 2

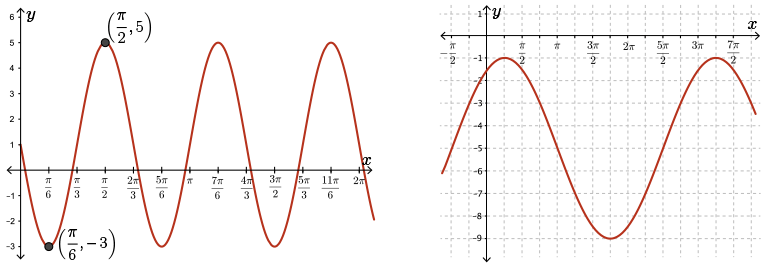
A sinusoidal function is defined for \(x \geq 0\). The first minimum occurs as \(\left(\dfrac{\pi}{6} , -3\right)\) and the first maximum occurs at \(\left(\dfrac{\pi}{2} , 5\right)\). Determine a possible equation for this function.

Solution

\(k\) is the average of the maximum and minimum values. So, \(k = 1\) and the vertical displacement is \(1\). The central horizontal axis is \(y=1\).

The amplitude is \(\dfrac{5 - (-3)}{2} = 4\) so \(\lvert a \rvert = 4\).

At this point, we can calculate \(\lvert b \rvert\).

Recall that period \(= \dfrac{2\pi}{\lvert b \rvert}\). After rearranging, \(\lvert b \rvert = \dfrac{2\pi}{\text{period}} = \dfrac{2\pi}{\dfrac{2\pi}{3}} = 3\).

We still must decide which sinusoidal function to model with.

From our work, we know that \(\lvert a \rvert = 4, \lvert b \rvert = 3,\) the period is \(\dfrac{2\pi}{3},\) and \(k = 1\).

As you can see, there's a variety of choices for how we model this function. In this case, the last one is probably the simplest.

Check Your Understanding B

This question is not included in the Alternative Format, but can be accessed in the Review section of the side navigation.

Lesson Part 3

Examples

Example 3

Solution

First, we will determine the maximum and minimum values.

Two consecutive maximum points are \(\left(\dfrac{\pi}{4},-1\right)\) and \(\left(\dfrac{13\pi}{4},-1\right)\). By using the difference between the \(x\)-coordinates of these two consecutive maximum points, we determine that the period is \(\dfrac{13\pi}{4} - \dfrac{\pi}{4} = 3\pi\).

It follows that \(\lvert b \rvert = \dfrac{2\pi}{3\pi} = \dfrac{2}{3}\).

We can plot key points on the graph: maximum points, minimum points, and points on the central horizontal axis: \(\left(-\dfrac{\pi}{2},-5\right)\), \(\left(\dfrac{\pi}{4},-1\right)\), \(\left(\pi,-5\right)\), \(\left(\dfrac{7\pi}{4},-9\right)\), \(\left(\dfrac{5\pi}{2},-5\right)\), and \(\left(\dfrac{13\pi}{4},-1\right)\).

We can read the phase shift from the graph and select an appropriate sinusoidal function.

• For a phase shift \(h = -\dfrac{\pi}{2}, a = 4, b = \dfrac{2}{3}, k = -5,\) and \(y = 4\sin\left[\dfrac{2}{3}\left(x + \dfrac{\pi}{2}\right)\right] - 5\).
• For a phase shift \(h = \dfrac{\pi}{4}, a = 4, b = \dfrac{2}{3}, k = -5,\) and \(y = 4\cos\left[\dfrac{2}{3}\left(x - \dfrac{\pi}{4}\right)\right] - 5\).
• For a phase shift \(h = \pi, a = -4, b = \dfrac{2}{3}, k = -5,\) and \(y = -4\cos\left[\dfrac{2}{3}\left(x - \pi \right)\right] - 5\).
• For a phase shift \(h = \dfrac{7\pi}{4}, a = -4, b = \dfrac{2}{3}, k = -5,\) and \(y = -4\cos\left[\dfrac{2}{3}\left(x - \dfrac{7\pi}{4}\right)\right] - 5\).

There are also other equations that we can obtain by choosing different phase shifts.

Check Your Understanding C

This question is not included in the Alternative Format, but can be accessed in the Review section of the side navigation.

Example 4

In the previous example, we developed several equations which could be used to model the given information.

Once we have an equation, we are generally interested in obtaining more information, either from the graph or from the equation.

Solution

From the graph, we can see that a maximum of \(-1\) occurs when \(x = \dfrac{\pi}{4}\).

From our earlier work, we know that the period is \(3\pi\).

Therefore, the maximum value \(-1\) occurs when

Example 5

Using the equation \(y = 4\sin\left[\dfrac{2}{3}\left(x + \dfrac{\pi}{2}\right)\right] - 5\), determine all possible values of \(x\) such that the value of the sinusoidal function is a maximum.

Solution

From the equation, we see that \(a = 4\), \(b = \dfrac{2}{3}\), \(h = -\dfrac{\pi}{2}\), and \(k = -5\). Using \(a = 4\) and \(k=-5\), the maximum value is \(-5 + 4= -1\), as we saw from the graph. The period is \(\dfrac{2\pi}{\lvert b \rvert} = \dfrac{2\pi}{\dfrac{2}{3}} = 3\pi\).

The angle \(\dfrac{2}{3}\left(x + \dfrac{\pi}{2}\right)\) looks a bit complex so we can simplify if we let \(A = \dfrac{2}{3}\left(x + \dfrac{\pi}{2}\right)\).

We know from our experience that for \(y = \sin(A)\), a maximum occurs when \(A = \dfrac{\pi}{2}\).

Multiplying both sides of the equation by \(\dfrac{3}{2}\) and simplifying, we get

Since we know that the period is \(3\pi\) radians and that a maximum occurs when \(x= \dfrac{\pi}{4}\), the maximum value \(-1\) occurs when \(x = \dfrac{\pi}{4} + 3 \pi n, n \in \mathbb{Z}\). So, we get the same result that we saw before.

This same approach will also work to determine when the minimum values or middle values occur. The middle values are the values that occur on the central horizontal axis.

But what if we want other values? We can approximate from the graph or solve the sinusoidal equation for the required values.

Lesson Part 4

Examples

Let's look at a slightly different example.

Example 6

Determine the values of \(x, 0 \leq x \leq 3\pi\) so that \(y = 4\sin\left[\dfrac{2}{3}\left(x + \dfrac{\pi}{2}\right)\right]-5\) equals \(-3\).

Solution

The angle \(\dfrac{2}{3}\left(x + \dfrac{\pi}{2}\right)\) looks a bit complex so we can simplify if we let \(A = \dfrac{2}{3}\left(x + \dfrac{\pi}{2}\right)\).

We will solve an equation which is much more straightforward.

We know, from our work with special triangles, that the reference angle is \(\dfrac{\pi}{6}\) and \(\sin\left(A\right) \gt 0\) in quadrants \(1\) and \(2\). It follows that \(A = \dfrac{\pi}{6}\) in quadrant \(1\) and \(A = \pi - \dfrac{\pi}{6} = \dfrac{5\pi}{6}\) in quadrant \(2\).

Since \(A = \dfrac{2}{3}\left(x + \dfrac{\pi}{2}\right)\), we know that

We want \(0 \leq x \leq 3\pi\) and, from earlier work, we know that the period of \(y = 4\sin\left[\dfrac{2}{3}\left(x + \dfrac{\pi}{2}\right)\right] - 5\) is \(3\pi\).

The solution \(x = -\dfrac{\pi}{4}\) is not in the domain, but the coterminal angle \(x = - \dfrac{\pi}{4} + 3\pi = \dfrac{11\pi}{4}\) is in the domain.

The other solution \(x = \dfrac{3\pi}{4}\) is already in the required domain.

Adding or subtracting \(3\pi\) to either of these solutions takes us outside the domain.

Therefore, the only solutions are \(x = \dfrac{3\pi}{4}\) and \(x = \dfrac{11\pi}{4}\).

Summary

In this module, we developed equations to model situations which were defined by information given about a function or by a sketch of a function.

We used the graph of the function and the equation to obtain more information about the function.

We used the sketches to read information and we solved some trigonometric equations.

In a future module, we will look at applications which can be modelled with sinusoidal functions.