Compound Angle Formulas Alternative Format
Lesson Part 1
In This Module
- We will extend our knowledge of the fundamental trigonometric identities to include the compound angle identities shown here.\[\sin\left(A + B\right) =\sin(A)\cos(B) + \cos(A)\sin(B)\]\[\sin\left(A - B\right) =\sin(A)\cos(B) - \cos(A)\sin(B)\]\[\cos\left(A + B\right) =\cos(A)\cos(B) - \sin(A)\sin(B)\]\[\cos\left(A - B\right) =\cos(A)\cos(B) + \sin(A)\sin(B)\]\[\tan\left(A + B\right) =\dfrac{\tan(A) + \tan(B)}{1 - \tan(A)\tan(B)}\]\[\tan\left(A - B\right) =\dfrac{\tan(A) - \tan(B)}{1 + \tan(A)\tan(B)}\]
These identities involve the sum and difference of two angles and are often referred to as formulas as they provide a means of
- simplifying trigonometric expressions and proving other identities,
- determining exact values for angles related to the acute angles \(\dfrac{\pi}{12}\) or \(\dfrac{5\pi}{12}\) \(\left(15^{\circ} \right.\) or \(\left. 75^{\circ} \right)\), and
- solving certain trigonometric equations.
Derivation
We will begin by deriving the formula for \(\cos\left(A + B \right)\) using the unit circle.
Consider the two points \(P\) and \(Q\) on the unit circle, where \(P\) is defined by \(\left( \cos(\theta) , \sin(\theta) \right)\) for some angle \(\theta\), \(\theta \gt 0\) and \(Q\) is given by \(\left(\cos(-\beta) , \sin(-\beta)\right)\) for some angle \(\beta\), \(\beta \gt 0\). Now, applying our understanding of the symmetry with the sine and cosine functions, the coordinates of \(Q\) can be simplified to \(\left(\cos(\beta) , -\sin(\beta)\right)\).
The measure of \(\angle POQ\), with \(O\) at the origin, is \(\theta + \beta\).
The length of the line segment \(PQ\), denoted \(\lvert PQ \rvert \), can be found using the distance formula:
\[\lvert PQ \rvert = \sqrt{(\Delta x)^2 + (\Delta y)^2}\]
where \(\Delta x\) and \(\Delta y\) represent change in \(x\) and \(y\), respectively.
If we substitute the coordinates of \(P\) and \(Q\) into the distance formula, then expand and simplify, we can obtain an expression for the length of the line segment \(PQ\):
\[ \begin{align*} \lvert PQ \rvert &= \sqrt{(\cos(\theta) - \cos(\beta))^2+(\sin(\theta) - (-\sin(\beta)))^2} \\ &= \sqrt{(\cos(\theta) - \cos(\beta))^2+(\sin(\theta) + \sin(\beta))^2} \\ &= \sqrt{\cos^2(\theta) - 2\cos(\theta)\cos(\beta) + \cos^2(\beta) + \sin^2(\theta) + 2\sin(\theta)\sin(\beta) + \sin^2(\beta)} \\ &= \sqrt{{\color{BrickRed}\cos^2(\theta) + \sin^2(\theta)} + {\color{NavyBlue}\cos^2(\beta) + \sin^2(\beta)} - 2\cos(\theta)\cos(\beta) + 2\sin(\theta)\sin(\beta)} \\ &= \sqrt{{\color{BrickRed}1} + {\color{NavyBlue}1} - 2\cos(\theta)\cos(\beta) + 2\sin(\theta)\sin(\beta)} \\ &= \sqrt{{\color{BrickRed}2} - 2\cos(\theta)\cos(\beta) + 2\sin(\theta)\sin(\beta)} \end{align*} \]
Now rotate the points \(P\) and \(Q\) counterclockwise about the origin by angle of \(\beta\) to obtain \({\color{NavyBlue}Q'(1,0)}\) and \({\color{NavyBlue}P'~(\cos(\theta + \beta) , \sin(\theta + \beta))}\) on the unit circle, as shown in the diagram.
As a condition of the rotation, \(\angle P'OQ' = \angle POQ = \theta + \beta\) and \(\vert P'Q' \rvert = \lvert PQ \rvert\).
Now, substitute the coordinates of \(P'\) and \(Q'\) into the distance formula. Then, expand and simplify to obtain an expression for the length of \(P'Q'\):
\[ \begin{align*} \lvert P'Q' \rvert &= \sqrt{(\cos(\theta + \beta) - 1)^2 + (\sin(\theta + \beta) - 0)^2} \phantom{Math Rocks!} \\ &= \sqrt{\cos^2(\theta + \beta) - 2\cos(\theta + \beta) + 1 + \sin^2(\theta + \beta)} \\ &= \sqrt{{\color{BrickRed}\cos^2(\theta + \beta) + \sin^2(\theta + \beta)} - 2\cos(\theta + \beta) + 1} \\ &= \sqrt{{\color{BrickRed}1} - 2\cos(\theta + \beta) + 1} \\ &= \sqrt{2 - 2\cos(\theta + \beta)} \end{align*} \]
Since \(\lvert P'Q' \rvert = \lvert PQ \rvert\), we have
\[ \begin{align*} \sqrt{2 - 2(\cos(\theta + \beta))} &= \sqrt{2 - 2\cos(\theta)\cos(\beta) + 2\sin(\theta)\sin(\beta)} \\ {\color{BrickRed}2} - 2(\cos(\theta + \beta)) &= {\color{BrickRed}2} - 2\cos(\theta)\cos(\beta) + 2\sin(\theta)\sin(\beta) \\ -2(\cos(\theta + \beta)) &= -2\cos(\theta)\cos(\theta) + 2\sin(\theta)\sin(\beta) \\ \cos(\theta + \beta) &= \cos(\theta)\cos(\beta) - \sin(\theta)\sin(\beta) \end{align*} \]
We will refer to this identity as the angle sum formula for cosine.
Angle Sum Formula for Cosine
\(\cos(A+B) = \cos(A)\cos(B) - \sin(A)\sin(B)\)
It may also be called the addition formula for cosine. We can now use this formula as a basis to derive the other five compound angle formulas stated earlier.
Lesson Part 2
Derivation
To obtain the formula for \(\cos(\theta - \beta)\), we can express it as \(\cos(\theta + (-\beta))\) and apply the angle sum formula: \(\cos(A + B) = \cos(A)\cos(B) - \sin(A)\sin(B)\).
By setting \(A = \theta\) and \(B = -\beta\), we have
\[ \begin{align*} \cos(\theta - \beta) &= \cos({\color{BrickRed}\theta} + ({\color{NavyBlue}-\beta})) \\ &= \cos({\color{BrickRed}\theta})\cos({\color{NavyBlue}-\beta}) - \sin({\color{BrickRed}\theta})\sin({\color{NavyBlue}-\beta}) \end{align*} \]
We know by symmetry that \(\cos(-\beta)=\cos(\beta)\), cosine is an even function, and \(\sin(-\beta)=-\sin(\beta)\), sine is an odd function. So, this expression simplifies to
\[ \begin{align*} \cos(\theta - \beta) &= \cos(\theta)\cos(\beta) - \sin(\theta)(-\sin(\beta)) \\ &= \cos(\theta)\cos(\beta) + \sin(\theta)\sin(\beta) \end{align*} \]
which we will refer to as the angle difference formula for cosine.
Angle Difference Formula for Cosine
\(\cos(A - B) = \cos(A)\cos(B) + \sin(A)\sin(B)\)
The angle difference formula for cosine is similar to the angle sum formula for cosine
Angle Sum Formula for Cosine
\(\cos(A+B) = \cos(A)\cos(B) - \sin(A)\sin(B)\)
developed previously. Both formulas have the terms \(\cos(A)\cos(B)\) and \(\sin(A)\sin(B)\). In the difference formula, we have the sum of these terms. In the sum formula, we have the difference of the terms. Noting these similarities and differences may help you when trying to recall these formulas.
To obtain the formula for \(\sin(\theta + \beta)\) we can use the cofunction identities,
\[\sin(x) = \cos\left(\dfrac{\pi}{2} - x\right) \text{ and } \cos(x) = \sin\left(\dfrac{\pi}{2} - x\right)\]
and apply the angle difference formula for cosine, \(\cos(A - B) = \cos(A)\cos(B) + \sin(A)\sin(B)\). We begin with
\[ \begin{align*} \sin(\theta + \beta) &= \cos\left({\color{BrickRed}\dfrac{\pi}{2}}-({\color{NavyBlue}\theta + \beta})\right) \end{align*} \]
and regroup the terms of the angle to get
\[ \begin{align*} \sin(\theta + \beta) &= \cos\left(\left({\color{BrickRed}\dfrac{\pi}{2} - \theta}\right) - {\color{NavyBlue}\beta}\right) \end{align*} \]
Now, apply the angle difference formula for cosine and simplify to determine the angle sum formula for sine. If we set \(A = {\color{BrickRed}\dfrac{\pi}{2} - \theta}\) and \(B = {\color{NavyBlue}\beta}\) in the angle difference formula for cosine, we get
\[ \begin{align*} \sin(\theta + \beta) &=\cos\left({\color{BrickRed}\dfrac{\pi}{2}-\theta}\right)\cos{\color{NavyBlue}(\beta)}+\sin\left({\color{BrickRed}\dfrac{\pi}{2}-\theta}\right)\sin{\color{NavyBlue}(\beta)} \end{align*} \]
Making appropriate substitutions with the cofunction identities, we obtain the angle sum formula for sine:
\[ \begin{align*} \sin(\theta + \beta) &= \sin(\theta)\cos(\beta) + \cos(\theta)\sin(\beta) \end{align*} \]
Here is the complete simplification procedure when all steps are put together:
\[ \begin{align*} \sin(\theta + \beta) &= \cos\left({\color{BrickRed}\dfrac{\pi}{2}}-({\color{NavyBlue}\theta + \beta})\right) \\ &= \cos\left(\left({\color{BrickRed}\dfrac{\pi}{2} - \theta}\right) - {\color{NavyBlue}\beta}\right) \\ &=\cos\left({\color{BrickRed}\dfrac{\pi}{2}-\theta}\right)\cos{\color{NavyBlue}(\beta)}+\sin\left({\color{BrickRed}\dfrac{\pi}{2}-\theta}\right)\sin{\color{NavyBlue}(\beta)} \\ &= \sin(\theta)\cos(\beta) + \cos(\theta)\sin(\beta) \end{align*} \]
Angle Sum Formula for Sine
\(\sin(A + B) = \sin(A)\cos(B) + \cos(A)\sin(B)\)
The angle difference formula can be derived in a similar way and will be left as an exercise question.
Angle Difference Formula for Sine
\(\sin(A - B) = \sin(A)\cos(B) - \cos(A)\sin(B)\)
Again, these two formulas are somewhat similar. Both formulas work with the terms \(\sin(A)\cos(B)\) and \(\cos(A)\sin(B)\). In the sum formula, note that we have the sum of the terms, whereas in the difference formula, we have the difference in the terms.
The final set of compound angle formulas involve tangent. To derive the angle sum formula for tangent, we begin by using the quotient identity.
\[ \begin{align*} \tan(A+B) &= \dfrac{\sin(A+B)}{\cos(A+B)} \end{align*} \]
We can now apply the angle sum formulas for sine and cosine:
\[ \begin{align*} \tan(A+B) &= \dfrac{\sin(A)\cos(B) + \cos(A)\sin(B)}{\cos(A)\cos(B)-\sin(A)\sin(B)} \\ \end{align*} \]
Then, to create tangent ratios, we will divide the terms in the numerator and denominator by \(\cos(A)\cos(B)\) and simplify:
\[ \begin{align*} \tan(A+B) &= \dfrac{(\sin(A)\cos(B) + \cos(A)\sin(B))\div {\color{BrickRed}\cos(A)\cos(B)}}{(\cos(A)\cos(B) - \sin(A)\sin(B))\div {\color{BrickRed}\cos(A)\cos(B)}} \\ &= \dfrac{\dfrac{\sin(A)\cancel{\cos(B)}}{\color{BrickRed}\cos(A)\cancel{\cos(B)}}+\dfrac{\cancel{\cos(A)}\sin(B)}{\color{BrickRed}\cancel{\cos(A)}\cos(B)}}{\dfrac{\cancel{\cos(A)\cos(B)}}{\color{BrickRed}\cancel{\cos(A)\cos(B)}}-\dfrac{\sin(A)\sin(B)}{\color{BrickRed}\cos(A)\cos(B)}} \\ &= \dfrac{\tan(A) + \tan(B)}{1 - \tan(A)\tan(B)} \end{align*} \]
This is the angle sum formula for tangent.
Angle Sum Formula for Tangent
\(\tan(A+B) = \dfrac{\tan(A) + \tan(B)}{1 - \tan(A)\tan(B)}\)
The angle difference formula for the tan ratio can be developed in a similar way and is left as an exercise question.
Angle Difference Formula for Tangent
\(\tan(A-B) = \dfrac{\tan(A)-\tan(B)}{1+ \tan(A)\tan(B)}\)
Once again, it may be worth noting the similarities and differences in these two formulas.
Summary
Angle Sum Formulas
\(\sin(A+B) = \sin(A)\cos(B) + \cos(A)\sin(B)\)
\(\cos(A+B) = \cos(A)\cos(B) - \sin(A)\sin(B)\)
\(\tan(A+B) = \dfrac{\tan(A) + \tan(B)}{1 - \tan(A)\tan(B)}\)
Angle Difference Formulas
\(\sin(A-B) = \sin(A)\cos(B) - \cos(A)\sin(B)\)
\(\cos(A - B) = \cos(A)\cos(B) + \sin(A)\sin(B)\)
\(\tan(A-B) = \dfrac{\tan(A) - \tan(B)}{1+\tan(A)\tan(B)}\)
Will you need to memorise all of these compound angle formulas? It will help to be familiar with them as you move into the study of calculus. If you understand the connection between the formulas, how one formula can be derived from another, you may be able to use this knowledge to help recall a specific formula when needed.
Now that we have established these formulas, let's consider some of the ways they can be applied to manipulate trigonometric expressions and solve problems.
Lesson Part 3
Examples
Example 1 — Part A
Determine an equivalent trigonometric expression for
\[\sin\left(x - \dfrac{\pi}{2}\right) \phantom{\left(\dfrac{1}{1}\right)}\]
using an appropriate compound angle formula.
Solution
Using the angle difference formula,
\[\sin(A-B) = \sin(A)\cos(B) - \cos(A)\sin(B)\]
By setting \(A = x\) and \(B = \dfrac{\pi}{2}\), we have
\[ \begin{align*} \sin\left(x - \dfrac{\pi}{2}\right) &= \sin(x)\cos\left(\dfrac{\pi}{2}\right) - \cos\left(x\right)\sin\left(\dfrac{\pi}{2}\right) \\ &= \sin(x)(0) - \cos(x)(1) \\ &= -\cos(x) \end{align*} \]
Previously, we may have argued that
\[ \begin{align*} \sin\left(x - \dfrac{\pi}{2}\right) &= \sin\left(-\left(\dfrac{\pi}{2} - x\right)\right) \\ &= -\sin\left(\dfrac{\pi}{2} - x\right) \\ &= -\cos(x) \end{align*} \]
using the fact that the sine function is an odd function, then making a substitution using an appropriate cofunction identity.
Example 1 — Part B
Determine an equivalent trigonometric expression for
\[\cos\left(x+\dfrac{3\pi}{2}\right)\]
using an appropriate compound angle formula.
Solution
Using the angle sum formula
\[\cos(A+B) = \cos(A)\cos(B) - \sin(A)\sin(B)\]
and substituting \(A=x\) and \(B=\dfrac{3\pi}{2}\), we have
\[ \begin{align*} \cos\left(x+\dfrac{3\pi}{2}\right) &= \cos(x)\cos\left(\dfrac{3\pi}{2}\right) - \sin(x)\sin\left(\dfrac{3\pi}{2}\right) \\ &= \cos(x)(0) - \sin(x)(-1) \\ &= \sin(x) \end{align*} \]
Equivalent forms similar to these were discussed in the previous module and verified using transformations.
To verify this equivalence graphically, translate \(y = \cos(x)\) to the left \(\dfrac{3\pi}{2}\) units.
The image curve is the sine curve.
With the compound angle formulas, we now have a way of proving these identities algebraically.
Example 1 — Part C
Determine an equivalent trigonometric expression for
\[\tan\left(x + \dfrac{5\pi}{6}\right)\]
using an appropriate compound angle formula.
Solution
Using \(\tan(A+B) = \dfrac{\tan(A)+\tan(B)}{1 - \tan(A)\tan(B)}\), where \(A = x\) and \(B = \dfrac{5\pi}{6}\), we have
\[ \begin{align*} \tan\left({\color{BrickRed}x} + {\color{NavyBlue}\dfrac{5\pi}{6}}\right) &= \dfrac{\tan({\color{BrickRed}x}) + \tan\left({\color{NavyBlue}\frac{5\pi}{6}}\right)}{1 - \tan({\color{BrickRed}x})\tan\left({\color{NavyBlue}\frac{5\pi}{6}}\right)} \end{align*} \]
Now we need to evaluate \(\tan\left(\dfrac{5\pi}{6}\right)\).
The angle \(\dfrac{5\pi}{6}\) has a terminal arm in the second quadrant, where \(\tan\) is negative, and a reference angle of \(\dfrac{\pi}{6}\).

So, \(\tan\left(\dfrac{\pi}{6}\right)=\dfrac{1}{\sqrt{3}}\). Thus, \(\tan\left(\dfrac{5\pi}{6}\right)=-\dfrac{1}{\sqrt{3}}\).
Using these values, we can simplify the expression:
\[ \begin{align*} \tan\left({\color{BrickRed}x} + {\color{NavyBlue}\dfrac{5\pi}{6}}\right) &= \dfrac{\tan({\color{BrickRed}x}) + \tan\left({\color{NavyBlue}\frac{5\pi}{6}}\right)}{1 - \tan({\color{BrickRed}x})\tan\left({\color{NavyBlue}\frac{5\pi}{6}}\right)} \\ &= \dfrac{\tan(x) - \frac{1}{\sqrt{3}}}{1 - \tan(x)\left(-\frac{1}{\sqrt{3}}\right)} \\ &= \dfrac{\left(\tan(x) - \frac{1}{\sqrt{3}}\right)}{\left(1 + \frac{\tan(x)}{\sqrt{3}}\right)} \times \dfrac{\sqrt{3}}{\sqrt{3}} \\ &= \dfrac{\sqrt{3} \tan(x) - 1}{\sqrt{3} + \tan(x)} \end{align*} \]
We can go in the reverse direction with these formulas in order to simplify certain trigonometric expressions.
Example 2 — Part A
Express \(\cos(\theta)\cos(2\theta) - \sin(\theta)\sin(2\theta)\) as a single trigonometric ratio using an appropriate compound angle formula.
Solution
Simplification of this expressions is straightforward once you've connected the pattern with the correct compound angle formula.
Using the sum formula for cosine,
\[\cos(A+B) = \cos(A)\cos(B) - \sin(A)\sin(B)\]
where \(A = \theta\) and \(B = 2\theta\), we have
\[ \begin{align*} \cos(\theta)\cos(2\theta) - \sin(\theta)\sin(2\theta) &= \cos(\theta + 2\theta) \\ &= \cos(3\theta) \end{align*} \]
Example 2 — Part B
Simplification of this expressions is also straightforward once you've connected the pattern with the correct compound angle formula.
Express \(\dfrac{\tan\left(\frac{\pi}{3}\right)-\tan\left(\frac{3\pi}{4}\right)}{1+\tan\left(\frac{\pi}{3}\right)\tan\left(\frac{3\pi}{4}\right)}\) as a single trigonometric ratio using an appropriate compound angle formula.
Solution
Using the difference formula for tangent,
\[\tan(A - B) = \dfrac{\tan(A) - \tan(B)}{1 + \tan(A)\tan(B)}\]
where \(A = \frac{\pi}{3}\) and \(B = \frac{3\pi}{4}\), we have
\[ \begin{align*} \dfrac{\tan\left(\frac{\pi}{3}\right) - \tan\left(\frac{3\pi}{4}\right)}{1 + \tan\left(\frac{\pi}{3}\right)\tan\left(\frac{3\pi}{4}\right)} &=\tan\left(\frac{\pi}{3} - \frac{3\pi}{4}\right) \\ &= \tan\left(\frac{4\pi}{12}-\frac{9\pi}{12}\right) \\ &= \tan\left(-\frac{5\pi}{12}\right) \\ &= -\tan\left(\frac{5\pi}{12}\right) \end{align*} \]
Example 2 — Part C
Express \(\dfrac{1}{2}\cos(x) + \dfrac{\sqrt{3}}{2}\sin(x)\) as a single trigonometric ratio using an appropriate compound angle formula.
Solution 1
To simplify this expression, we must identify an angle and trig ratios that produce the factors \(\dfrac{1}{2}\) and \(\dfrac{\sqrt{3}}{2}\) found in the expression.
Since \(\sin\left(\dfrac{\pi}{6}\right) = \dfrac{1}{2}\) and \(\cos\left(\dfrac{\pi}{6}\right) = \dfrac{\sqrt{3}}{2}\), we can substitute these ratios into the given expression and simplify using the angle sum formula for sine:
\[ \begin{align*} \dfrac{1}{2}\cos(x) + \dfrac{\sqrt{3}}{2}\sin(x) &= \sin\left(\dfrac{\pi}{6}\right)\cos(x) + \cos\left(\dfrac{\pi}{6}\right)\sin(x) \\ &= \sin\left(\dfrac{\pi}{6}+x\right) \end{align*} \]
Solution 2
An alternate expression can be obtained using \(\sin\left(\dfrac{\pi}{3}\right) = \dfrac{\sqrt{3}}{2}\) and \(\cos\left(\dfrac{\pi}{3}\right) = \dfrac{1}{2}\).\[ \begin{align*} \dfrac{1}{2}\cos(x) + \dfrac{\sqrt{3}}{2}\sin(x) &= \cos\left(\dfrac{\pi}{3}\right)\cos(x) + \sin\left(\dfrac{\pi}{3}\right)\sin(x) \\ &= \cos\left(\dfrac{\pi}{3}-x\right) \end{align*} \]
exercising the angle difference formula for cosine.
This implies that \(\sin\left(\dfrac{\pi}{6}+x\right) = \cos\left(\dfrac{\pi}{3} - x\right)\).
To verify \(\sin\left(\dfrac{\pi}{6} + x\right) = \cos\left(\dfrac{\pi}{3}-x\right)\) graphically, let \(f(x) = \sin\left(\dfrac{\pi}{6}+x\right)\) and \(g(x) = \cos\left(\dfrac{\pi}{3} - x\right)\).
The graph of \(f(x) = \sin\left(x + \dfrac{\pi}{6}\right)\) can be obtained by translating the graph of \(y = \sin(x)\) to the left \(\dfrac{\pi}{6}\).
The graph of \(g(x) = \cos\left(-\left(x - \dfrac{\pi}{3}\right)\right)\) can be obtained by first reflecting the graph of \(y = \cos(x)\) in the \(y\)-axis, which does nothing to change the graph since the cosine function is even.
Then, we translate the curve \(g(x)=\cos(-x)\) to the right \(\dfrac{\pi}{3}\).
The graph of \(f(x)\) is identical to the graph of \(g(x)\).
Check Your Understanding A
This question is not included in the Alternative Format, but can be accessed in the Review section of the side navigation.
Lesson Part 4
Examples
We can use compound angle formulas to determine the exact value of any angle corresponding to the reference angles \(15^{\circ}\) and \(75^{\circ}\), or in radians, \(\frac{\pi}{12}\) and \(\frac{5\pi}{12}\).
Example 3 — Part A
Determine the exact value of \(\sin\left(\dfrac{13\pi}{12}\right)\) using a compound angle formula.
Solution
To determine the exact value of \(\sin\left(\dfrac{13\pi}{12}\right)\), we express \(\dfrac{13\pi}{12}\) as a sum or difference of two angles corresponding to the related acute angles \(\dfrac{\pi}{6}\), \(\dfrac{\pi}{4}\), or \(\dfrac{\pi}{3}\). We use these angles since we know their exact value from the special triangles studied previously. For example,
\[ \begin{align*} \dfrac{13\pi}{12} &= \dfrac{9\pi}{12} + \dfrac{4\pi}{12} \\ &= \dfrac{3\pi}{4} + \dfrac{\pi}{3} \end{align*} \]
So, \(\sin\left(\dfrac{13\pi}{12}\right) = \sin\left(\dfrac{3\pi}{4} + \dfrac{\pi}{3}\right)\).
Now, applying the angle sum formula for sine and determining the exact value of each trig ratio on the expression, we can obtain the exact value for this expression:
\[ \begin{align*} \sin\left(\dfrac{13\pi}{12}\right) &= \sin\left(\dfrac{3\pi}{4} + \dfrac{\pi}{3}\right) \\ &= \sin\left(\dfrac{3\pi}{4}\right)\cos\left(\dfrac{\pi}{3}\right) + \cos\left(\dfrac{3\pi}{4}\right)\sin\left(\dfrac{\pi}{3}\right) \\ &= \left(\dfrac{1}{\sqrt{2}}\right)\left(\dfrac{1}{2}\right) + \left(-\dfrac{1}{\sqrt{2}}\right)\left(\dfrac{\sqrt{3}}{2}\right) \\ &= \dfrac{1-\sqrt{3}}{2\sqrt{2}} \end{align*} \]
By multiplying both the numerator and denominator by \(\sqrt{2}\), we get
\[ \begin{align*} \sin\left(\dfrac{13\pi}{12}\right) &= \dfrac{1-\sqrt{3}}{2\sqrt{2}} = \dfrac{1 - \sqrt{3}}{2\sqrt{2}} {\color{BrickRed}\times \dfrac{\sqrt{2}}{\sqrt{2}}} = \dfrac{\sqrt{2} - \sqrt{6}}{4} \end{align*} \]
Mathematicians often eliminate radical factors from denominators. This is called rationalising the denominator. The answer in either form is correct, but the second form is a more common final answer.
Therefore, the exact value of \(\sin\left(\dfrac{13\pi}{12}\right)\) is
\[\dfrac{\sqrt{2} - \sqrt{6}}{4}\]
Example 3 — Part B
Express \(195^{\circ}\) degrees as a sum or difference of angles related to the acute angles of \(30^{\circ}\), \(45^{\circ}\), or \(60^{\circ}\) degrees. Then, determine the exact value of \(\cos\left(195^{\circ}\right)\) using a compound angle formula.
Solution
Two solutions to this example are presented. Both solutions presented here may be different from your approach. However, your final answer should be the same. The first solution uses the angle difference formula and the second one uses the angle sum formula. Many different combinations of angles related to \(30^{\circ}\), \(45^{\circ}\), or \(60^{\circ}\) degrees can be used to form \(195^{\circ}\) degrees.
Solution 1
Since \(195^{\circ} = 225^{\circ} - 30^{\circ}\)
\[ \begin{align*} \cos(195^{\circ}) &= \cos(225^{\circ} - 30^{\circ}) \\ &= \cos(225^{\circ})\cos(30^{\circ}) + \sin(225^{\circ})\sin(30^{\circ}) \\ &= \left(-\frac{1}{\sqrt{2}}\right)\left(\frac{\sqrt{3}}{2}\right) + \left(-\frac{1}{\sqrt{2}}\right)\left(\frac{1}{2}\right) \\ &= \dfrac{-\sqrt{3}-1}{2\sqrt{2}} \\ &= \dfrac{-\sqrt{6} - \sqrt{2}}{4} \end{align*} \]
Solution 2
Since \(195^{\circ} = 135^{\circ} + 60^{\circ}\)
\[ \begin{align*} \cos(195^{\circ}) &=\cos(135^{\circ} + 60^{\circ}) \\ &= \cos(135^{\circ})\cos(60^{\circ}) - \sin(135^{\circ})\sin(60^{\circ}) \\ &= \left(-\frac{1}{\sqrt{2}}\right)\left(\frac{1}{2}\right) - \left(\frac{1}{\sqrt{2}}\right)\left(\frac{\sqrt{3}}{2}\right) \\ &= \dfrac{-1-\sqrt{3}}{2\sqrt{2}} \\ &= \dfrac{-\sqrt{2} - \sqrt{6}}{4} \end{align*} \]
Check Your Understanding B
This question is not included in the Alternative Format, but can be accessed in the Review section of the side navigation.
Examples Continued
We can now use the compound angle formulas as well to prove identities.
Example 4
Prove that \(\cos(x + y)\cos(x - y) = \cos^2(x) - \sin^2(y)\).
Solution
We begin by applying the angle sum and difference formulas for cosine:
\[ \begin{align*} \text{L.S.} &= \cos(x+y)\cos(x-y) \\ &= \Big(\cos(x)\cos(y) - \sin(x)\sin(y)\Big)\Big(\cos(x)\cos(y) + \sin(x)\sin(y)\Big) \end{align*} \]
Then, expand to determine the product of the two expressions:
\[ \begin{align*} \text{L.S.} &= \Big(\cos(x)\cos(y)\Big)^2 + \cancel{\cos(x)\cos(y)\sin(x)\sin(y)} \\ &- \cancel{\sin(x)\sin(y)\cos(x)\cos(y)} - \Big(\sin(x)\sin(y)\Big)^2 \\ &= \Big(\cos(x)\cos(y)\Big)^2 - \Big(\sin(x)\sin(y)\Big)^2 \\ \end{align*} \]
Let's take note of where we were headed. The expression on the right side of the identity is in terms of \(\cos^2(x)\) and \(\sin^2(y)\). So this is a clue to replace \(\cos^2(y)\) and \(\sin^2(x)\) with their equivalent forms using the Pythagorean identities:
\[ \begin{align*} \text{L.S.} &= \cos^2(x)\cos^2(y) - \sin^2(x)\sin^2(y) \\ &= \cos^2(x)\Big(1 - \sin^2(y)\Big) - \Big(1 - \cos^2(x)\Big)\sin^2(y) \\ \end{align*} \]
We then expand and simplify again to obtain
\[ \begin{align*} \text{L.S.} &= \cos^2(x) - \cancel{\cos^2(x)\sin^2(y)} - \sin^2(y) + \cancel{\cos^2(x)\sin^2(y)} \\ &= \cos^2(x) - \sin^2(y) \\ &= \text{R.S.} \end{align*} \]
Here is the complete simplification procedure when all steps are put together:
\[ \begin{align*} \text{L.S.} &= \cos(x+y)\cos(x-y) \\ &= \Big(\cos(x)\cos(y) - \sin(x)\sin(y)\Big)\Big(\cos(x)\cos(y) + \sin(x)\sin(y)\Big) \\ &= \Big(\cos(x)\cos(y)\Big)^2 + \cancel{\cos(x)\cos(y)\sin(x)\sin(y)} \\ & - \cancel{\sin(x)\sin(y)\cos(x)\cos(y)} - \Big(\sin(x)\sin(y)\Big)^2 \\ &= \Big(\cos(x)\cos(y)\Big)^2 - \Big(\sin(x)\sin(y)\Big)^2 \\ &= \cos^2(x)\cos^2(y) - \sin^2(x)\sin^2(y) \\ &= \cos^2(x)\Big(1 - \sin^2(y)\Big) - \Big(1 - \cos^2(x)\Big)\sin^2(y) \\ &= \cos^2(x) - \cancel{\cos^2(x)\sin^2(y)} - \sin^2(y) + \cancel{\cos^2(x)\sin^2(y)} \\ &= \cos^2(x) - \sin^2(y) \\ &= \text{R.S.} \end{align*} \]
Therefore, \(\cos(x + y)\cos(x - y) = \cos^2(x) - \sin^2(y)\).
Example 5
Solve for \(x\) in \(\dfrac{1}{\sin\left(x - \dfrac{\pi}{6}\right) - \sin\left(x + \dfrac{\pi}{6}\right)} = \sqrt{2}\), where \(0 \leq x \leq 2\pi\).
Solution
We begin by applying the angle sum and difference formulas for sine to the terms in the denominator:
\[ \begin{align*} \dfrac{1}{\sin\left(x - \frac{\pi}{6}\right) - \sin\left(x + \frac{\pi}{6}\right)} &= \sqrt{2} \\ \dfrac{1}{\left(\sin(x)\cos\left(\frac{\pi}{6}\right) - \cos(x)\sin\left(\frac{\pi}{6}\right)\right) - \left(\sin(x)\cos\left(\frac{\pi}{6}\right) + \cos(x)\sin\left(\frac{\pi}{6}\right)\right)} &= \sqrt{2} \end{align*} \]
We can then simplify this subsequent expression by adding and subtracting the terms:
\[ \begin{align*} \dfrac{1}{\sin(x)\cos\left(\frac{\pi}{6}\right) - \cos(x)\sin\left(\frac{\pi}{6}\right) - \sin(x)\cos\left(\frac{\pi}{6}\right) - \cos(x)\sin\left(\frac{\pi}{6}\right)} &= \sqrt{2} \\ \dfrac{1}{-\cos(x)\sin\left(\frac{\pi}{6}\right) - \cos(x)\sin\left(\frac{\pi}{6}\right)} &= \sqrt{2} \\ \dfrac{1}{-2\cos(x)\sin\left(\frac{\pi}{6}\right)} &= \sqrt{2} \\ \end{align*} \]
Substituting \(\sin\left(\dfrac{\pi}{6}\right)=\dfrac{1}{2}\) allows us to simplify further:
\[ \begin{align*} \dfrac{1}{-2\cos(x)\left(\frac{1}{2}\right)} &=\sqrt{2} \\ \dfrac{1}{-\cos(x)} &= \sqrt{2} \\ \end{align*} \]
Rearranging this equation, we isolate \(x\):
\[ \begin{align*} -\sqrt{2}\cos(x) &= 1 \\ \cos(x) &= -\dfrac{1}{\sqrt{2}} \end{align*} \]
We are now ready to solve for \(x\). The ratio \(\dfrac{1}{\sqrt{2}}\) indicates that the angle \(x\) has a reference angle of \(\dfrac{\pi}{4}\). Cosine is negative for angles with terminal arms in the second or third quadrants.
Therefore,
\[ \begin{align*} x &= \pi-\dfrac{\pi}{4} \text{ or } \pi+\dfrac{\pi}{4} \\ &= \dfrac{3\pi}{4} \text{ or } \dfrac{5\pi}{4} \end{align*} \]
These two solutions are the only solutions in the specified interval \([0,2\pi]\).
Here is the complete simplification procedure when all steps are put together:
\[ \begin{align*} \dfrac{1}{\sin\left(x - \frac{\pi}{6}\right) - \sin\left(x + \frac{\pi}{6}\right)} &= \sqrt{2} \\ \dfrac{1}{\left(\sin(x)\cos\left(\frac{\pi}{6}\right) - \cos(x)\sin\left(\frac{\pi}{6}\right)\right) - \left(\sin(x)\cos\left(\frac{\pi}{6}\right) + \cos(x)\sin\left(\frac{\pi}{6}\right)\right)} &= \sqrt{2} \\ \dfrac{1}{\sin(x)\cos\left(\frac{\pi}{6}\right) - \cos(x)\sin\left(\frac{\pi}{6}\right) - \sin(x)\cos\left(\frac{\pi}{6}\right) - \cos(x)\sin\left(\frac{\pi}{6}\right)} &= \sqrt{2} \\ \dfrac{1}{-\cos(x)\sin\left(\frac{\pi}{6}\right) - \cos(x)\sin\left(\frac{\pi}{6}\right)} &= \sqrt{2} \\ \dfrac{1}{-2\cos(x)\sin\left(\frac{\pi}{6}\right)} &= \sqrt{2} \\ \dfrac{1}{-2\cos(x)\left(\frac{1}{2}\right)} &=\sqrt{2} \\ \dfrac{1}{-\cos(x)} &= \sqrt{2} \\ -\sqrt{2}\cos(x) &= 1 \\ \cos(x) &= -\dfrac{1}{\sqrt{2}} \\ x &=\dfrac{3\pi}{4} \ \text{or} \ \dfrac{5\pi}{4} \end{align*} \]
Lesson Part 5
Examples
In this final example, we will use a compound angle formula to solve a trigonometric equation involving both the \(\cos(x)\) and \(\sin(x)\) ratios.
Example 6
Solve \(\sqrt{3}\sin(x) + 3\cos(x) = -\sqrt{6}, 0 \leq x \leq 2\pi\) by first expressing \(\sqrt{3}\sin(x) + 3\cos(x)\) in the form \(a \sin(x - h)\).
Solution
First, find a value for \(a\) and \(h\) such that \(\sqrt{3}\sin(x) + 3\cos(x) = a\sin(x - h)\).
We start by applying the difference formula for sine to the expression on the right-hand side of the equation.
\[ \begin{align*} \sqrt{3}\sin(x) + 3\cos(x) &= a\sin(x - h) \\ &= a\Big(\sin(x)\cos(h) - \cos(x)\sin(h)\Big) \\ &= a\sin(x)\cos(h) - a\cos(x)\sin(h) \\ \sqrt{3}\, {\color{BrickRed}\sin(x)} + 3\, {\color{NavyBlue}\cos(x)} &= a\, {\color{BrickRed}\sin(x)}\cos(h) - a\, {\color{NavyBlue}\cos(x)}\sin(h) \end{align*} \]
Now, for the left side of the equation to equal the right side for all values of \(x\), then the coefficients of the \(\sin(x)\) terms found on opposite sides of the equation must be equal. As well, the coefficients of the two \(\cos(x)\) terms must also be equal. This will give us two equations for our two unknowns:
\[ \begin{align*} a\cos(h) &= \sqrt{3} \tag{1} \\ -a\sin(h) &=3 \tag{2} \end{align*} \]
We use these two equations to solve for the two unknowns \(a\) and \(h\).
Dividing equation \((2)\) by equation \((1)\),
\[ \begin{align*} \dfrac{-a\sin(h)}{a\cos(h)} &= \dfrac{3}{\sqrt{3}} \\ -\tan(h) &= \dfrac{3}{\sqrt{3}} \\ \tan(h) &= -\dfrac{3}{\sqrt{3}} \times {\color{BrickRed}\dfrac{\sqrt{3}}{\sqrt{3}}} \\ \tan(h) &= -\sqrt{3} \end{align*} \]
and therefore, \(h = \dfrac{2\pi}{3}\) is one possible solution since \(\tan\left(\dfrac{\pi}{3}\right)=\dfrac{\sqrt{3}}{1}\) and tangent is negative in the second quadrant.
We need only one value for \(h\); substituting \(h = \dfrac{2\pi}{3}\) into \((1)\),
\[ \begin{align*} a\cos\left(\dfrac{2\pi}{3}\right) &= \sqrt{3} \\ a\left(-\dfrac{1}{2}\right) &= \sqrt{3} \\ a &= -2\sqrt{3} \end{align*} \]
Therefore, \(\sqrt{3}\sin(x) + 3\cos(x) =-2\sqrt{3}\sin\left(x - \dfrac{2\pi}{3}\right)\).
Substituting this form into \(\sqrt{3}\sin(x) + 3\cos(x) = -\sqrt{6}\), we have
\[-2\sqrt{3}\sin\left(x - \dfrac{2\pi}{3}\right) = -\sqrt{6}\]
We are now ready to solve for \(x\) by first isolating \(\sin\left(x - \dfrac{2\pi}{3}\right)\).
\[ \begin{align*} \sin\left(x - \dfrac{2\pi}{3}\right) &= -\dfrac{\sqrt{6}}{-2\sqrt{3}} \\ &= \dfrac{\sqrt{2}}{2} \ \text{or} \ \dfrac{1}{\sqrt{2}} \end{align*} \]
So the angle \(x - \dfrac{2\pi}{3}\) corresponds to the reference angle \(\dfrac{\pi}{4}\) and has a terminal arm in the first or second quadrant since the value of sine is positive. So, the two principal angles for
\[ x - \dfrac{2\pi}{3} = \dfrac{\pi}{4}, \ \dfrac{3\pi}{4} \]
Adding integer multiples of \(2 \pi\) to create coterminal angles will provide all possible solutions. So, all possible solutions for \(x - \dfrac{2\pi}{3}\) are given by \(\dfrac{\pi}{4} + 2\pi n\) and \(\dfrac{3\pi}{4} + 2\pi n\) where \(n \in \mathbb{Z}\).
It is only the two principal angles that produce values for \(x\) in the specified domain \([0,\ 2\pi]\). So, for \(0 \leq x \leq 2\pi\), we have
\[ \begin{align*} x - \dfrac{2\pi}{3} &= \dfrac{\pi}{4}, \ \dfrac{3\pi}{4} \\ x &= \dfrac{\pi}{4} + \dfrac{2\pi}{3}, \ \dfrac{3\pi}{4} + \dfrac{2\pi}{3} \\ x &= \dfrac{3\pi}{12} + \dfrac{8\pi}{12}, \ \dfrac{9\pi}{12} + \dfrac{8\pi}{12} \\ x &= \dfrac{11\pi}{12}, \dfrac{17\pi}{12} \end{align*} \]
Therefore, the solutions to \(\sin\left(x - \dfrac{2\pi}{3}\right)=\dfrac{1}{\sqrt{2}}\) and the original equation, \(\sqrt{3}\sin(x) + 3\cos(x) = -\sqrt{6}\), for \(0 \leq x \leq 2\pi\), are \(\dfrac{11\pi}{12} , \dfrac{17\pi}{12}\).
We were able to solve \(\sqrt{3}\sin(x) + 3\cos(x) = -\sqrt{6}\) by first determining an equivalent expression for \(\sqrt{3}\sin(x) + 3\cos(x)\) using an appropriate compound angle formula.
We can verify this equivalence and the solutions to the equation using graphing technology.
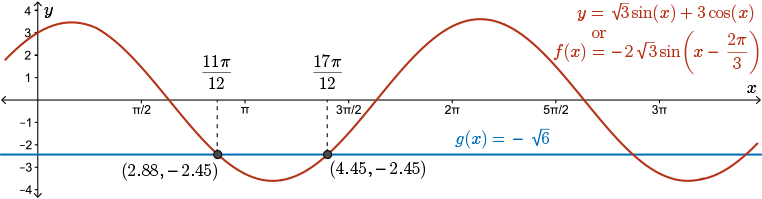
The graph of \(y = \sqrt{3}\sin(x) + 3\cos(x)\) is the same as the graph of \(y = -2\sqrt{3}\sin\left(x - \dfrac{2\pi}{3}\right)\) and this graph intersects the line \(y = -\sqrt{6}\) at approximately \(2.88\) and \(4.45\), or \(\dfrac{11\pi}{12}\) and \(\dfrac{17\pi}{12}\).
Summary
We have six new identities. You may memorise only the sum formulas as the difference formulas can be obtained from the sum formulas by changing the sign.
Angle Sum Formulas
\(\sin(A+B) = \sin(A)\cos(B) + \cos(A)\sin(B)\)
\(\cos(A+B) = \cos(A)\cos(B) - \sin(A)\sin(B)\)
\(\tan(A+B) = \dfrac{\tan(A) + \tan(B)}{1 - \tan(A)\tan(B)}\)
Angle Difference Formulas
\(\sin(A-B) = \sin(A)\cos(B) - \cos(A)\sin(B)\)
\(\cos(A - B) = \cos(A)\cos(B) + \sin(A)\sin(B)\)
\(\tan(A-B) = \dfrac{\tan(A) - \tan(B)}{1+\tan(A)\tan(B)}\)
Compound angle formulas can be used to
- simplify trigonometric expressions and determine equivalent forms,
- prove identities,
- find exact values for angles related to the acute angles \(\dfrac{\pi}{12}\) and \(\dfrac{5\pi}{12}\), and
- solve trigonometric equations.