Partial Solutions

1. Using \( 1-2 \sin^2{(A)} = \cos{(2A)} \),\[\begin{align*} 1-2 \sin^2{\left(\dfrac{11\pi}{8}\right)} &= \cos{\left(\dfrac{11\pi}{4}\right)} \\ &= \cos{\left(\dfrac{3\pi}{4}\right)} \\ &= -\dfrac{1}{\sqrt{2}} \text { or } -\dfrac{\sqrt{2}}{2} \\ \end{align*}\]
2. Using \( 2\cos^2{(A)} - 1=\cos{(2A)} \),\[\begin{align*} 1 - 2\cos^2{(105^\circ)} &= -(2\cos^2{(105^\circ)} - 1) \\ &= -(\cos{(210^\circ)}) \\ &= -\left(-\dfrac{\sqrt{3}}{2}\right) \\ &= \dfrac{\sqrt{3}}{2} \\ \end{align*}\]
3. Using \( 2\sin{(A)}\cos{(A)}=\sin{(2A)} \),\[\begin{align*} 4 \sin{(112.5^\circ)}\cos{(112.5^\circ)} &= 2\left(2 \sin{(112.5^\circ)}\cos{(112.5^\circ)}\right)\\ &= 2\sin{(225^\circ)} \\ &= 2\left(-\dfrac{1}{\sqrt{2}}\right) \\ &= 2\left(-\dfrac{\sqrt{2}}{2}\right) \\ &= -\sqrt{2} \\ \end{align*}\]
4. Since \( \dfrac{2\tan{\left(A\right)}}{1-\tan^2{\left(A\right)}}=\tan{(2A)} \) then \( \dfrac{1-\tan^2{\left(A\right)}}{2\tan{\left(A\right)}}=\cot{(2A)} \). Thus,\[\begin{align*} \dfrac{1-\tan^2{\left(\dfrac{\pi}{12}\right)}}{\tan{\left(\dfrac{\pi}{12}\right)}} &= 2\left(\dfrac{1-\tan^2{\left(\dfrac{\pi}{12}\right)}}{2\tan{\left(\dfrac{\pi}{12}\right)}}\right) \\ &= 2\cot{\left(\dfrac{\pi}{6}\right)} \\ &= 2\sqrt{3} \\ \end{align*}\]
5. Rearranging \( \cos{(2A)}=2 \cos^2{\left(A\right)}-1 \) to \( \cos^2{\left(A\right)}=\dfrac{\cos{(2A)}+1}{2} \), we have\[\begin{align*} \cos^2\left(\dfrac{11\pi}{12}\right) &= \dfrac{\cos\left(\dfrac{11\pi}{6}\right) + 1}{2} \\ &= \dfrac{\dfrac{\sqrt{3}}{2} + 1}{2} \times \frac{2}{2} \\ &= \dfrac{\sqrt{3}+2}{4} \\ \end{align*}\]

1. From the diagram below, \( \cos{(\theta)} = -\dfrac{\sqrt{7}}{4} \).

   

   Thus, \( \sin{(2\theta)}=2\sin{(\theta)}\cos{(\theta)}=2\left(\dfrac{3}{4}\right)\left(-\dfrac{\sqrt{7}}{4}\right)=-\dfrac{3\sqrt{7}}{8} \).

2.  \[\begin{align*} \cos{(2\theta)} &= -\dfrac{7}{8} \\ 2\cos^2{(\theta)} - 1 &= -\dfrac{7}{8} \\ 2\cos^2{(\theta)} &= \dfrac{1}{8} \\ \cos{(\theta)} &= \pm \dfrac{1}{4} \end{align*}\]However \( \pi \lt 2\theta \lt \dfrac{3\pi}{2} \), so \( \dfrac{\pi}{2} \lt \theta \lt \dfrac{3\pi}{4} \) and \( \cos{(x)} \lt 0 \). Thus, \( \cos{(\theta)} = -\dfrac{1}{4} \). From the diagram below, \( \sin{(\theta)}=\dfrac{\sqrt{15}}{4} \).

   

   Thus, \( \cos{(\theta)}=-\dfrac{1}{4} \) and \( \sin{(\theta)}=\dfrac{\sqrt{15}}{4} \).

1. Rearranging the double angle formula, \( \cos{(2A)}=2\cos^2{\left(A\right)}-1 \), we have\[\cos{(A)}=\pm\sqrt{\frac{\cos{(2A)}+1}{2}}\] Since \( \cos{(22.5^\circ)} \gt 0 \), then\[\begin{align*} \cos{(22.5^\circ)} &= \sqrt{\frac{\cos{(45^\circ)}+1}{2}} \\ &= \sqrt{\dfrac{\frac{\sqrt{2}}{2}+1}{2} \times \frac{2}{2}} \\ &= \sqrt{\dfrac{\sqrt{2}+2}{4}} \\ &= \dfrac{\sqrt{\sqrt{2}+2}}{2} \end{align*}\]
2. Rearranging the double angle formula, \( \cos{(2A)}=1-2\sin^2{\left(A\right)} \), we have\[\sin{(A)}=\pm\sqrt{\frac{1-\cos{(2A)}}{2}}\] Since \( \sin{\left(\dfrac{7\pi}{12}\right)} \gt 0 \), then\[\begin{align*} \sin{\left(\dfrac{7\pi}{12}\right)} &= \sqrt{\frac{1-\cos{\left(\tfrac{7\pi}{6}\right)}}{2}} \\ &= \sqrt{\frac{1-\left(-\tfrac{\sqrt{3}}{2}\right)}{2} \times \frac{2}{2} } \\ &= \sqrt{\dfrac{2+\sqrt{3}}{4}} \\ &= \dfrac{\sqrt{2+\sqrt{3}}}{2} \end{align*}\]
3. Since \( \cos{(A)} = \pm\sqrt{\dfrac{\cos{(2A)}+1}{2}} \) and \( \sin{(A)} = \pm\sqrt{\dfrac{1-\cos{(2A)}}{2}} \), and \( \tan{ \left(\dfrac{5\pi}{8}\right) } = \dfrac{ \sin{ \left( \tfrac{5\pi}{8} \right) } }{ \cos{\left( \tfrac{5\pi}{8} \right) } } \) where \( \sin{ \left( \dfrac{5\pi}{8} \right)} \gt 0 \) and \( \cos{\left( \dfrac{5\pi}{8} \right)} \lt 0 \), then\[\begin{align*} \tan{\left(\dfrac{5\pi}{8}\right)} &= \dfrac{\sqrt{\frac{1-\cos{\left( \frac{5\pi}{4} \right)}}{2}}}{-\sqrt{\frac{\cos{\left( \frac{5\pi}{4} \right)}+1}{2}}}\\ &= -\sqrt{\frac{1-\cos{\left(\frac{5\pi}{4}\right)}}{2} \times \frac{2}{\cos{\left(\frac{5\pi}{4}\right)}+1}}\\ &= -\sqrt{\dfrac{1-\cos{\left(\frac{5\pi}{4}\right)}}{\cos{\left(\frac{5\pi}{4}\right)}+1}}\\ &= -\sqrt{\dfrac{1-\left(-\frac{1}{\sqrt{2}}\right)}{\left(-\frac{1}{\sqrt{2}}\right)+1} \times \frac{\sqrt{2}}{\sqrt{2}}}\\ &= -\sqrt{\dfrac{\sqrt{2}+1}{-1+\sqrt{2}}} \\ &= -\sqrt{\dfrac{\left(\sqrt{2}+1\right)\left(\sqrt{2}+1\right)}{\left(\sqrt{2}-1\right)\left(\sqrt{2}+1\right)}} \\ &= -\sqrt{3+2\sqrt{2}} \end{align*}\]

1.  \[\begin{align*} \sin (3 \theta) &= \sin(2 \theta + \theta)\\ &= \sin{(2\theta)}\cos{(\theta)}+\cos{(2\theta)}\sin{(\theta)}\\ &= 2\sin{(\theta)}\cos{(\theta)}\cos{(\theta)}+(1-2\sin^2{(\theta)})\sin{(\theta)}\\ &= 2\sin{(\theta)}\cos^2{(\theta)}+\sin{(\theta)}-2\sin^3{(\theta)}\\ &= 2\sin{(\theta)}(1-\sin^2{(\theta)})+\sin{(\theta)}-2\sin^3{(\theta)}\\ &= 2\sin{(\theta)}-2\sin^3{(\theta)}+\sin{(\theta)}-2\sin^3{(\theta)}\\ \therefore\sin{(3\theta)}&= 3\sin{(\theta)}-4\sin^3{(\theta)} \end{align*}\]
2.  \[\begin{align*} \cos{(4\theta)} &= 2\cos^2{(2\theta)} - 1 \\ &= 2(2\cos^2{(\theta)}-1)^2 - 1\\ &= 2(4\cos^4{(\theta)}-4\cos^2{(\theta)}+1) - 1\\ &= 8\cos^4{(\theta)}-8\cos^2{(\theta)}+1\\ \therefore\cos{(4\theta)}&= 8\cos^4{(\theta)}-8\cos^2{(\theta)}+1 \end{align*}\]
3.  \[\begin{align*} \cot{(2\theta)} &= \dfrac{\cos{(2\theta)}}{\sin{(2\theta)}}\\ &= \dfrac{\cos^2{(\theta)}-\sin^2{(\theta)}}{2\sin{(\theta)}\cos{(\theta)}} \end{align*}\] Dividing the numerator and denominator by \( \sin^2{(\theta)} \),\[\begin{align*} &= \dfrac{\tfrac{\cos^2{(\theta)}}{\sin^2{(\theta)}}-\tfrac{\sin^2{(\theta)}}{\sin^2{(\theta)}}}{\tfrac{2\sin{(\theta)}\cos{(\theta)}}{\sin^2{(\theta)}}}\\ &= \dfrac{\cot^2{(\theta)} - 1}{2\cot{(\theta)}}\\ \therefore \cot{(2\theta)} &= \dfrac{\cot^2{(\theta)} - 1}{2\cot{(\theta)}} \end{align*}\]

Sketching \( f(x)= 2\sin^2{(x)} \):

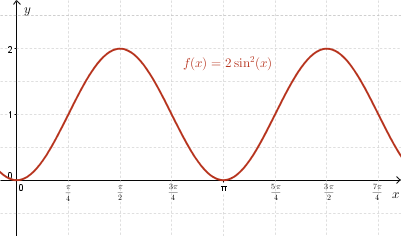
Rearranging \( \cos{(2x)}=1-2\sin^2{(x)} \), we have \( 2\sin^2{(x)}=-\cos{(2x)} +1 \); this implies that the graph of \( f(x)= 2\sin^2{(x)} \) is the same as the graph of \( y=-\cos{(2x)} +1 \).

Therefore, the graph of \( y=f(x) \) can be obtained by applying the following transformations to the graph of \( y=\cos{(x)} \):

• a reflection in the \( x \)-axis
• a horizontal stretch about the \( y \)-axis by a factor of \( \frac{1}{2} \)
• a vertical translation \( 1 \) unit upwards.

Sketching \( g(x)=3\sin{(2x)}\cos{(2x)}-1 \):

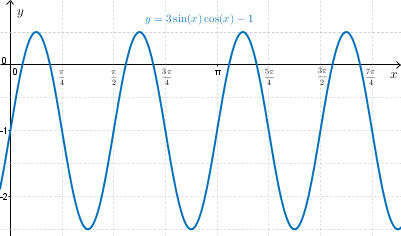
From \( \sin{(4x)}=2\sin{(2x)}\cos{(2x)} \), we have \( \sin{(2x)}\cos{(2x)}=\frac{1}{2}\sin{(4x)} \).

Substituting this into \( g(x)=3\sin{(2x)}\cos{(2x)}-1 \), we obtain \( g(x)=3\left(\frac{1}{2}\sin{(4x)}\right)-1 \) or \( g(x)=\frac{3}{2}\sin{(4x)}-1 \).

Therefore, the graph of \( y=g(x) \) can be obtained by applying the following transformations to the graph of \( y=\sin{(x)} \):

• a vertical stretch about the \( x \)-axis by a factor of \( \frac{3}{2} \)
• a horizontal stretch about the \( y \)-axis by a factor of \( \frac{1}{4} \)
• a vertical translation \( 1 \) unit downwards.