Solving Polynomial Inequalities Alternative Format

Lesson Part 1

We will begin by solving a linear inequality. This should be review for you. Consider the following example.

Solving Linear Inequalities

Review

Solve \( 5x - 3 \geq 7x - 9,\ x \in \mathbb{R} \).

Solution

The steps involved in solving a linear inequality are similar to the steps used to solve a linear equation, with one exception: when multiplying or dividing both sides of the inequality by a negative value, the inequality condition must be reversed.

When solving this given inequality, we rearrange the terms, collecting \(x\) terms to one side and the constant terms to the other side of the inequality.

\[ \begin{align*} 5x - 3 &\geq 7x - 9 \\ 5x - 7x &\geq -9 + 3 \\ -2x &\geq -6 \end{align*} \]

After simplifying each side, we must divide both sides by \(-2\) at which point we must reverse greater than and equal to to less than and equal to as shown here.

\[ \begin{align*} \dfrac{-2x}{-2} &\textcolor{BrickRed}{\leq}\dfrac{-6}{-2} \\ x &\leq 3 \end{align*} \]

Therefore, the solution to this inequality can be expressed in set notation as \(\{x \mid x \leq 3 ,\ x \in \mathbb{R}\} \).

The solution can also be stated using interval notation:
\(x\) is an element of the values from \(-\infty\) to \(3\) inclusive. \(x\) is an element of \( \mathbb{R} \).

\[x \in (-\infty, 3],\ x \in \mathbb{R}\]

The square bracket is used to indicate the inclusion of \(3\). The round bracket around negative infinity is necessary since negative infinity is not a number but a concept.

It can also be represented graphically using a real number line as shown:

Solving Polynomial Inequalities

Let's now consider the steps required to solve higher degree polynomial inequalities. Our first example is a quadratic inequality. We will use an algebraic approach to solve this inequality.

Example 1

Solve \( x^2 - 3x \gt 10,\ x \in \mathbb{R} \).

Algebraic Solution

We begin as we do with a quadratic equation: bring all terms of the inequality to one side, leaving zero on the other side. Then, we factor the quadratic.

\[ \begin{align*} x^2 - 3x - 10 & \gt 0 \\ (x - 5)(x + 2) & \gt 0 \end{align*} \]

Now, a product of two factors is positive in two cases.

Therefore, the solution to this quadratic inequality is \( \{x\mid x \lt -2 \text{ or } x \gt 5,\ x \in \mathbb{R}\} \).

In interval notation, this is \( x \in (-\infty, -2) \cup (5, \infty) \). This can also be illustrated using a number line as shown:

Image Description: A number line has a open circle at \(-2\) with an arrow extending in the direction of \(-\infty\). There is another open circle at \(5\) with an arrow extending in the direction of \(\infty\).

Graphical Solution

We can also take a graphical approach to solving this inequality.

We begin the same way by rearranging the inequality.

\[ \begin{align*} x^2 - 3x & \gt 10 \\ x^2 - 3x - 10 & \gt 0 \\ (x - 5)(x + 2) & \gt 0 \end{align*} \]

We can now let \(f(x) = (x - 5)(x + 2)\) and graph this function.

To graph this function, we identify the zeros, or \(x\)-intercepts, as \(x = -2\) and \(x = 5\).

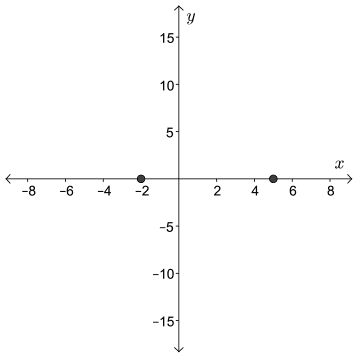
The leading coefficient is positive. So the parabola opens upward.

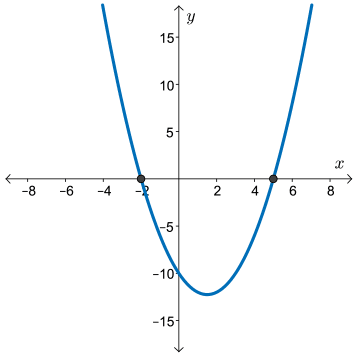
We make a quick sketch of the function since we need only determine when \(f(x)\) is greater than \(0\). That is we need to determine when the \(y\)-values are positive.

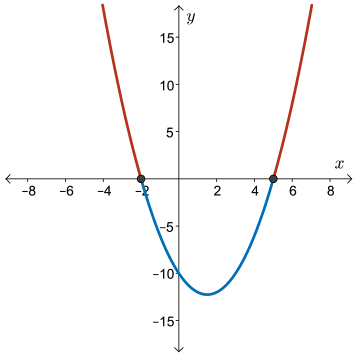
From the graph of \( f(x) = (x - 5)(x + 2) \), we see that \( f(x) \gt 0 \) (the graph is above the \( x \)-axis) when

\[ x \lt -2 \text{ or } x \gt 5 \]

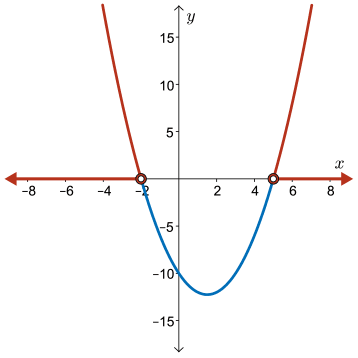
This confirms the solution found using an algebraic “case” approach.

Lesson Part 2

Solving Polynomial Inequalities

Example 2

Solve the cubic inequality \( 2x^2 - x^3 \geq 2 - x,\ x \in \mathbb{R} \).

Algebraic Solution

We begin by arranging the terms on one side of the inequality.

\[ \begin{align*} 2x^2-x^3 &\geq 2-x \\ -x^3+2x^2+x-2 &\geq 0 \end{align*} \]

We could have moved the terms to the right side of the inequality, thus avoiding the negative leading coefficient in this example. Or we could divide both sides of the inequality by \(-1\). When dividing by a negative value, it is necessary to reverse the inequality condition.

\[ x^3-2x^2-x+2 \textcolor{BrickRed}{\leq}0 \]

You may notice that this polynomial can be factored by grouping. If we do not use this method, we would need to employ the factor theorem to determine the first factor. We factor by grouping:

\[ \begin{align*} x^2(x - 2) - 1(x - 2) &\leq 0 \\ (x - 2)(x^2 - 1) &\leq 0 \\ (x - 2)(x - 1)(x + 1) &\leq 0 \end{align*} \]

• There are \(3\) factors: \( (x-2), (x-1) \), and \( (x+1) \). We need to detemine when the product of these three factors is less than or equal to zero.
• The product of these three factors will be zero when one of the factors is zero and the product will be negative when an odd number of the factors are negative.

There are several cases that must be considered. The case approached used previously becomes onerous.

Case 1	Case 2	Case 3	Case 4	Case 5	Case 6	Case 7	Case 8
\(x-2\lt 0\)	\(x-2\lt 0\)	\(x-2\lt 0\)	\(x-2\lt 0\)	\(x-2\gt 0\)	\(x-2\gt 0\)	\(x-2\gt 0\)	\(x-2\gt 0\)
\(x-1\lt 0\)	\(x-1\lt 0\)	\(x-1\gt 0\)	\(x-1\gt 0\)	\(x-1\lt 0\)	\(x-1\lt 0\)	\(x-1\gt 0\)	\(x-1\gt 0\)
\(x+1\lt 0\)	\(x+1\gt 0\)	\(x+1\lt 0\)	\(x+1\gt 0\)	\(x+1\lt 0\)	\(x+1\gt 0\)	\(x+1\lt 0\)	\(x+1\gt 0\)

Let's consider an algebraic approach that addresses all the cases using an organized table.

• The sign of the value of each linear factor changes at the “zero” value of the factor.
  • For example, \(x-2\) is positive when \(x \gt 2\) and negative when \(x \lt 2\).
• We begin by identifying the zero values for the factors: \( x = \pm 1\) and \(x = 2 \).
  • We will use these values to identify intervals where changes in the sign of the factors may occur.

\[ (x - 2)(x - 1)(x + 1) \leq 0 \]

In setting up the table, we list the zero values across the top in numerical order, then identify the intervals about these values, placing these intervals across the first row. List the factors in the first column. Now we are ready to fill in the table.

	\(x \lt -1\)	\(x=-1\)	\(-1 \lt x \lt 1\)	\(x=1\)	\(1 \lt x \lt 2\)	\(x=2\)	\(x \gt 2\)
\(x-2\)
\(x-1\)
\(x+1\)
\((x-2)(x-1)(x+1)\)

• We choose a test value from within each interval, substitute this value into each factor, and identify if the factor is positive or negative in that interval.
  • For the interval \(x \lt -1\), we use \(x=-2\) as a test value.
    • We substitute the value \(-2\) into each factor and determine the sign of the factor for that interval.
  • For the interval \(-1 \lt x \lt 1\), we use \(x=0\) as a test value.
  • For the interval \(1 \lt x \lt 2\), we use \(x=1.5\) as a test value.
  • For the interval \(x \gt 2\), we use \(x=3\) as a test value.
• We determine the sign of \((x-2)(x-1)(x+1)\) by determining the sign of the product of the factors. Remember, the product of an odd number of negative values is negative. Otherwise, the product is positive.

	\(x \lt -1\)	\(x=-1\)	\(-1 \lt x \lt 1\)	\(x=1\)	\(1 \lt x \lt 2\)	\(x=2\)	\(x \gt 2\)
\(x-2\)	\(-\)		\(-\)		\(-\)		\(+\)
\(x-1\)	\(-\)		\(-\)		\(+\)		\(+\)
\(x+1\)	\(-\)		\(+\)		\(+\)		\(+\)
\((x-2)(x-1)(x+1)\)	\(-\)		\(+\)		\(-\)		\(+\)

The solution to this inequality can now be identified.

The product of the factors, \((x-2)(x-1)(x+1) \lt 0\) when \(x \lt -1\) or when \(1 \lt x \lt 2\).

Since the product, \((x-2)(x-1)(x+1)\), can also equal \(0\), it is necessary to include the zero values in the solution.

Therefore, the solution is \( \{x\mid x \leq -1 \text{ or } 1 \leq x \leq 2,\ x \in \mathbb{R}\} \).

Again, the solution can be illustrated on the number line and expressed using interval notation.

\[ x \in (-\infty, -1] \cup [1, 2],\ x \in \mathbb{R} \]

Check Your Understanding A

This question is not included in the Alternative Format, but can be accessed in the Review section of the side navigation.

Graphical Solution

We will, again, look at a graphical solution to this inequality.

\[ \begin{align*} 2x^2 - x^3 &\geq 2 - x \\ -x^3 + 2x^2 + x - 2 &\geq 0 \\ x^3 - 2x^2 - x + 2 &\leq 0 \\ (x - 2)(x - 1)(x + 1) &\leq 0 \end{align*} \]

Once the terms of the inequality have been arranged to one side, we can then define a function, \(f(x)\), to equal the polynomial expression.

Let \( f(x) = (x - 2)(x - 1) (x + 1) \).

We will sketch the graph and determine when \( f(x) \leq 0 \).

• We identify the zeros: \( x = \pm 1\) and \( x = 2 \). All three zeros are of multiplicity one, so the graph will pass through each zero.
• Since the function is cubic with a positive leading coefficient, it will have “opposite” end behaviours with

\[ y \rightarrow -\infty \text{ as } x \rightarrow -\infty \]

and

\[ y \rightarrow \infty \text{ as } x \rightarrow \infty \]

We begin our sketch in the third quadrant, passing through each of the zeros and ending in the first quadrant.

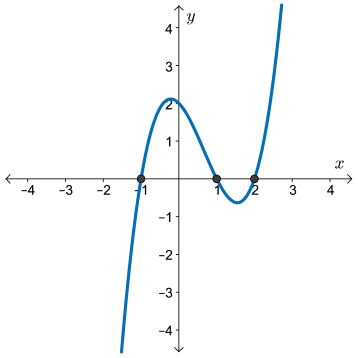
From the graph of \( f(x) = (x - 2)(x - 1)(x + 1) \), we see that \( f(x) \leq 0 \) when

\[x \leq -1 \text{ or } 1 \leq x \leq 2 \]

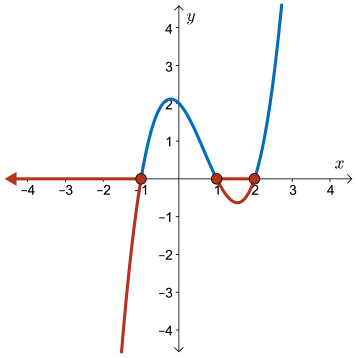
Therefore, the solution is

\[ \{x~|~x \leq -1 \text{ or } 1 \leq x \leq 2,\ x \in \mathbb{R}\} \]

Lesson Part 3

Solving Polynomial Inequalities

This next example will highlight other things to look for when solving inequalities. There is no need to manipulate this inequality algebraically. The terms of the polynomial are on the left side in factored form. And \(0\) is on the right.

Example 3

Solve \( -0.5x(x + 2)^2(x - 1)^3 \geq 0 \).

Graphical Solution

Let \( y = -0.5x(x + 2)^2(x - 1)^3 \).

• We have a \(6^{th}\) degree polynomial function with a negative leading coefficient. The graph will have “same” end behaviours with\[ y \rightarrow -\infty \text{ as } x \rightarrow \pm \infty \]
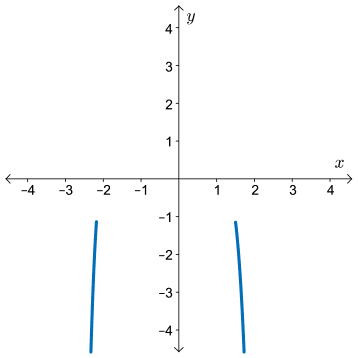
• There are \(3\) zeros:
  • A zero at \(x=-2\) of multiplicity two, resulting in a turning point at this zero.
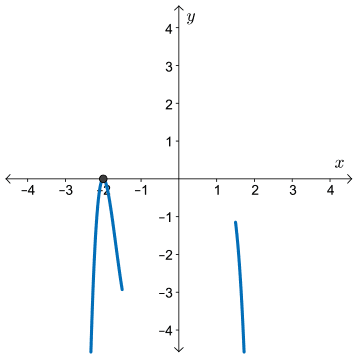
  • A zero at \(x=0\) of multiplicity one, so the curve will pass directly through the \(x\)-axis at the origin.
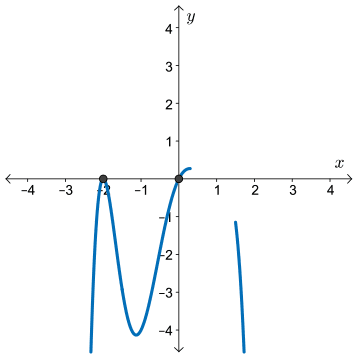
  • A zero of multiplicity three at \(x=1\), so the graph will pass through the \(x\)-axis with a point of inflection.

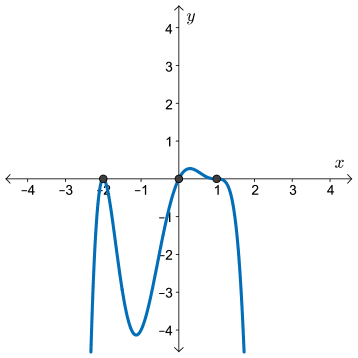
\[ y = -0.5x(x + 2)^2(x - 1)^3 \]

Using the graph, we see that \(y \geq 0\) (that is, the curve is on or above the \(x\)-axis) when

\[x=-2 \text{ or } 0 \leq x \leq 1\]

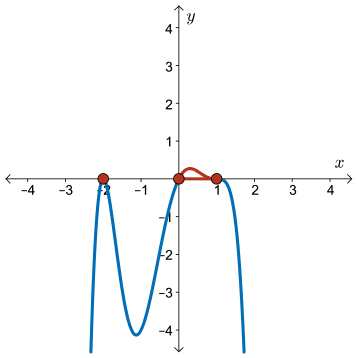
Therefore,

\[ -0.5x(x + 2)^2(x - 1)^3 \geq 0 \]

when

\[ x \in \{-2\} \cup [0, 1],\ x \in \mathbb{R} \]

Check Your Understanding B

This question is not included in the Alternative Format, but can be accessed in the Review section of the side navigation.

Algebraic Solution

To solve this problem algebraically we set up the table as shown.

	\(x \lt -2\)	\(x=-2\)	\(-2 \lt x \lt 0\)	\(x=0\)	\(0 \lt x \lt 1\)	\(x=1\)	\(x \gt 1\)
\(-0.5x\)
\((x+2)^2\)
\((x-1)^3\)
\(-0.5x(x+2)^2(x-1)^3\)

Note:

• We must include any constant factor, especially a negative constant, which will certainly affect the sign of the product.
• Factors of multiplicity greater than one can be grouped together.

An alternate approach for completing the table is to consider the sign of the factor for each interval, filling in the table one row at a time.

• The factor \(-0.5x\) has a zero value at \(x=0\), so it will change sign at \(x=0\). When \(x \lt 0\), it will be positive and for \( x \gt 0\), it will be negative.
• The factor \((x+2)^2\) will always be positive in these intervals because the value is squared.
• The factor \((x-1)^3\) will change signs at \(x=1\): negative when \(x \lt 1\) and positive when \(x \gt 1\).

	\(x \lt -2\)	\(x=-2\)	\(-2 \lt x \lt 0\)	\(x=0\)	\(0 \lt x \lt 1\)	\(x=1\)	\(x \gt 1\)
\(-0.5x\)	\(+\)		\(+\)		\(-\)		\(-\)
\((x+2)^2\)	\(+\)		\(+\)		\(+\)		\(+\)
\((x-1)^3\)	\(-\)		\(-\)		\(-\)		\(+\)
\(-0.5x(x+2)^2(x-1)^3\)

We now determine the sign of the \(-0.5x(x+2)^2 (x-1)^3\) by determining the product of the factors in each interval.

	\(x \lt -2\)	\(x=-2\)	\(-2 \lt x \lt 0\)	\(x=0\)	\(0 \lt x \lt 1\)	\(x=1\)	\(x \gt 1\)
\(-0.5x\)	\(+\)		\(+\)	\(0\)	\(-\)		\(-\)
\((x+2)^2\)	\(+\)	\(0\)	\(+\)		\(+\)		\(+\)
\((x-1)^3\)	\(-\)		\(-\)		\(-\)	\(0\)	\(+\)
\(-0.5x(x+2)^2(x-1)^3\)	\(-\)	\(0\)	\(-\)	\(0\)	\(+\)	\(0\)	\(-\)

Therefore, the solution to \( -0.5x(x + 2)^2(x - 1)^3 \geq 0 \) is \( \{x\mid x = -2 \text{ or } 0 \leq x \leq 1,\ x \in \mathbb{R} \} \)

Check Your Understanding C

This question is not included in the Alternative Format, but can be accessed in the Review section of the side navigation.

Lesson Part 4

Solving Polynomial Inequalities

Example 4

A cubic function, \(y=f(x)\), has a turning point at \((-2,0)\), an \(x\)-intercept at \(x=1\), and \(f(-1)=4\). Determine all values of \(x\) such that \( 0 \lt f(x) \lt 8\).

Many of the skills developed in this unit will be needed to solve this problem.

Solution

To determine the equation, we can use the zeros and an additional point on the curve.

• There is a zero at \( x = -2 \) of multiplicity two. Therefore, \((x + 2)^2 \) is a factor of the function.
• There is a zero at \( x = 1 \) of multiplicity one. Therefore, \((x - 1)\) is a factor of the function.

Let \(f(x)=a(x-1) (x+2)^2\).

Since \( f(-1) = 4 \), we can now substitute in the point \((-1, 4)\) to solve for a.

\[ \begin{align*} 4 & = a(-1 - 1)(-1 + 2)^2 \\ 4 & = a(-2)(1)^2 \\ a & = -2 \end{align*} \]

The equation of the function is therefore,

\[ f(x) = -2(x - 1)(x + 2)^2 \]

To determine all values of \( x \) such that \( 0 \lt f(x) \lt 8 \), solve \( 0 \lt -2(x - 1)(x + 2)^2 \lt 8 \).

This translates into solving the inequalities,

\[ 0 \lt -2(x - 1)(x + 2)^2 \text{ and } -2(x - 1)(x + 2)^2 \lt 8 \]

individually.

We solve \(-2(x-1) (x+2)^2 \gt 0\) graphically.

Therefore, \(\{x\mid x \lt 1, x \neq -2,\ x \in \mathbb{R} \} \).

Now, solve \( -2(x - 1)(x + 2)^2 \lt 8 \) algebraically.

We need to expand the terms on the left side of the inequality and bring all terms to one side with \(0\) on the other.

\[ \begin{align*} (-2x + 2)(x^2 + 4x + 4) & \lt 8 \\ -2x^3 - 8x^2 - 8x + 2x^2 + 8x + 8 & \lt 8 \\ -2x^3 - 6x^2 + 8 & \lt 8 \\ -2x^3 - 6x^2 & \lt 0 \end{align*} \]

We must then factor the polynomial expression.

\[-2x^2(x + 3) \lt 0 \]

We will then simplify this factored expression by dividing both sides of the inequality by \(-2\).

\[x^2(x + 3) \gt 0 \]

We can solve this inequality using an interval table.

	\(x \lt -3\)	\(x=-3\)	\(-3 \lt x \lt 0\)	\(x=0\)	\(x \gt 0\)
\(x^2\)	\(+\)		\(+\)	\(0\)	\(+\)
\(x+3\)	\(-\)	\(0\)	\(+\)		\(+\)
\(x^2(x+3)\)	\(-\)	\(0\)	\(+\)	\(0\)	\(+\)

Therefore, \(x^2(x + 3) \gt 0 \) when \( -3 \lt x \lt 0 \) or \( x \gt 0 \).

The solution to \( 0 \lt f(x) \lt 8 \) is all \( x \in \mathbb{R} \) such that \( x \lt 1, x \neq -2 \text{ and } x \gt -3, x \neq 0 \).

We now have two sets of conditions, which must be combined: \(f(x) \gt 0\) and \(f(x) \lt 8 \).

To determine which values of \(x\) satisfy both sets of conditions, it may be helpful to look at the solution of each inequality on a number line, as shown:

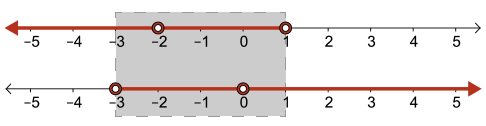
Since both sets of conditions must be satisfied, the grey area highlighting the overlap in the two sets of conditions helps us identify the solution.

Therefore, the solution is \( \{x\mid -3 \lt x \lt 1,\ x \neq -2,\ x \neq 0,\ x \in \mathbb{R} \} \).

Lesson Part 5

Solving Polynomial Inequalities

Example 5

Wire is bent to form the frame of a square-based rectangular prism. If \(36 \text{ cm}\) of wire is used, determine the restrictions on the length of the square base if the volume of the prism must be less than \(20 \text{ cm}^3 \).

Solution

We will begin by drawing a diagram of a square base rectangular prism.

Let \(x\) represent the length of the side of the square base \((x \gt 0)\) and \(h\) represent the height of the rectangular prism \((h \gt 0)\).

If \(36 \text{ cm}\) of wire is used to form the frame of the prism, then

\[ \begin{align*} 8x + 4h &= 36 \\ h &= 9 - 2x \end{align*} \]

Now the volume of the prism, given by the length times width times the height, is defined as

\[ \begin{align*} V(x) &= x^2h \\ V(x) &= x^2(9 - 2x) \end{align*} \]

To determine the restrictions on \( x \), we must solve for \( 0 \lt V(x) \lt 20 \). Specifically, the inequality is \( 0 \lt x^2(9 - 2x) \lt 20 \), which gives two inequalities to solve:

\[ 0 \lt x^2(9 - 2x) \text{ and } x^2(9 - 2x) \lt 20 \]

To solve for \( x^2(9 - 2x) \gt 0 \), we determine when \( 9 - 2x \gt 0 \) since \( x^2 \gt 0 \) for all \( x\neq 0 \).

\[ \begin{align*} 9 - 2x & \gt 0 \\ -2x & \gt -9 \\ x & \lt 4.5 \end{align*} \]

Therefore, \( x \lt 4.5 \), but \( x \gt 0 \), so \( 0 \lt x \lt 4.5 \).

Solve \( x^2(9 - 2x) \lt 20 \):

We must expand the terms on the left hand side and collect all terms to the left side of the inequality.

\[-2x^3 + 9x^2 - 20 \lt 0\]

Again, to make factoring easier, we will divide both sides of the inequality by \(-1\), remembering to reverse the inequality condition. This is done so the leading coefficient is positive.

\[ 2x^3 - 9x^2 + 20 \gt 0\]

We must now factor the cubic expression \(2x^3 - 9x^2 + 20\). We will use the factor theorem.

Let \( g(x) = 2x^3 - 9x^2 + 20 \).

We can now use long division, synthetic division, or the “have and need” method to find the corresponding factor.

Synthetic division is shown here,

\(2\)	\(2\)	\(-9\)	\(0\)	\(20\)
		\(4\)	\(-10\)	\(-20\)
	\(2\)	\(-5\)	\(-10\)	\(0\)

\[ g(x) = (x - 2)(2x^2 - 5x - 10) \]

The quadratic factor cannot be broken down any further.

Thus, it remains to find the zeros of \( g(x) = (x - 2)(2x^2 - 5x - 10) \).

We quickly identify \(x= 2\) and we use the quadratic formula to find the zeros from the quadratic factor.

\[ \begin{align*} x &= \dfrac{5 \pm \sqrt{(-5)^2 - 4(2)(-10)}}{2(2)} \\ x &= \dfrac{5 \pm \sqrt{105}}{4} \\ x &\approx -1.31, 3.81 \end{align*} \]

So, \( 0 \lt V(x) \lt 20 \) when \( x \) satisfies

\[( 0 \lt x \lt 4.5 ) \ \text{and} \ \left( \dfrac{5 - \sqrt{105}}{4} \lt x \lt 2 \text{ or } x \gt \dfrac{5 + \sqrt{105}}{4} \right) \]

Again, we will use a number line representation of these solutions to help us solve the overall inequality. The grey area here shows us the set of values of \(x\) that satisfy both conditions.

Therefore,

\[0 \lt x \lt 2 \text{ or } \dfrac{5 + \sqrt{105}}{4} \lt x \lt 4.5 \]

---

Another approach to determine when \(0 \lt V(x) \lt 20\) would be to graph \(y=V(x)\) and \(y=20\) and identify the values of \(x\) when the graph of \(y=V(x)\) is between \(y=20\) and the \(x\)-axis.

Note: \( V(x) = 20 \) at \( x = 2 \) and \( x = \dfrac{5 \pm \sqrt{105}}{4} \), and \( x \) is the side of the base, so we must remember that \( x \gt 0 \).

Studying the graph given, we can confirm the solution we had previously.

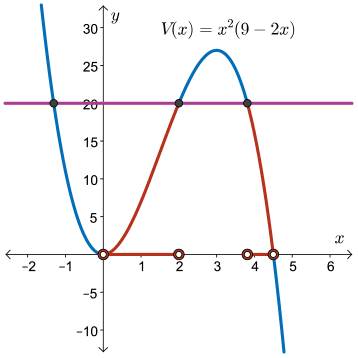
Image Description: A graph of the functions \(V(x) = x^2(9-2x)\) and \(V(x) = 20\). The only domain which match our restrictions, \(x \gt 0\) and \(V(x) \lt 20\), result in our solution.

Hence, \(0 \lt x \lt 2 \) or \( \dfrac{5 + \sqrt{105}}{4} \lt x \lt 4.5 \).

Therefore, the volume is between \(0\) and \( 20 \text{ cm}^3 \) when the length of the base is between \( 0 \text{ cm} \) and \( 2 \text{ cm} \), or between \( \frac{5 + \sqrt{105}}{4} \text{ cm } \) and \( 4.5 \text{ cm} \).

Presented here is a summary of the techniques used in this module to solve polynomial inequalities. You may wish to take some time to review these concepts.

Summary

• When multiplying or dividing both sides of the inequality by a negative value, the inequality condition must be reversed.
• When solving a factorable polynomial inequality of degree \(2\) or greater, arrange the terms to one side of the inequality condition, with \(0\) on the other side. Factor the polynomial expression to identify when the expression is equal to \(0\).
• An interval table can be created using the zeros and factors of the polynomial to help identify the intervals when the polynomial expression is positive or negative in value, thus determining the solution to the inequality.
• An alternate approach is to graph the corresponding polynomial function, using the factored expression, and identify the intervals when the graph is above (positive) or below (negative) the \(x\)-axis.
• Number lines can also be used to provide a visual aid when solving inequalities.