Right Triangle Terminology
A triangle that contains a right angle is called a right triangle.
Recall that the sum of the three angles in any triangle must be \(180^\circ\).
So consider a right triangle \(ABC\). If \(\angle A = 90^{\circ}\), which of the following is always true about \(\angle B\):
- less than \(90^{\circ}\)
- equal to \(90^{\circ}\)
- greater than \(90^{\circ}\)
Solution
Since the sum of the three angles must be \(180^{\circ}\), and since \(\angle A = 90^{\circ}\), we know that the sum of the remaining two angles must be \(90^\circ\). So,
\(\angle B + \angle C = 90^\circ\)
We conclude that both \(\angle B\) and \(\angle C\) must always be less than \(90^\circ\).
What this tells us is that in a right triangle, the \(90^\circ\) angle is the largest angle.
You might remember from an earlier geometry lesson that the largest side of a triangle is always opposite to the largest angle. And so we call the largest side of a right triangle the hypotenuse. The other two sides of the triangle are called legs. The two legs meet at the \(90^\circ\) angle.
Squares on the Sides of Right Triangles
Many thousands of years ago, a Greek mathematician named Pythagoras drew squares on the sides of a right triangle to examine the relationship between the side lengths of the triangle.
He drew these squares so that one side of the largest square is the hypotenuse of the right triangle, one side of the smallest square is the smallest side of the right triangle, and one side of the remaining square is the remaining side of the right triangle.
Pythagoras discovered that the areas of these three squares were related.
Use the following investigation to explore the relationship between the areas of the squares drawn on the three sides of a right triangle.
Explore This 1
Description
How does the sum of the areas of the two smaller squares relate to the area of the larger square?
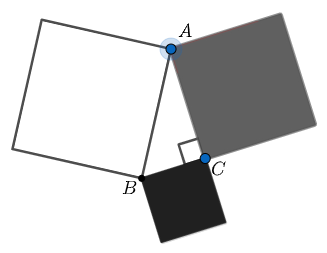
Observe the following steps.
Step 1
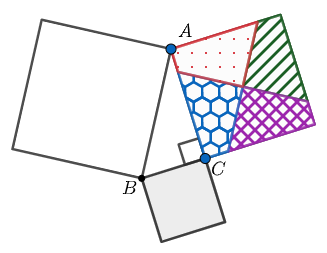
Step 2
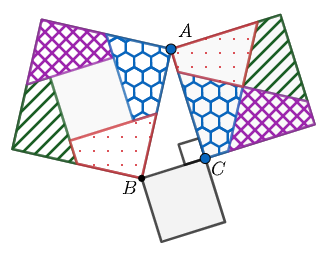
Created with GeoGebra. Author: University of Waterloo. CC BY-NC-SA 4.0.
Interactive Version
Explore Pythagorean Theorem
The Pythagorean Relationship
Did you notice that the five pieces that made up the smaller two squares also fit perfectly inside the larger square?
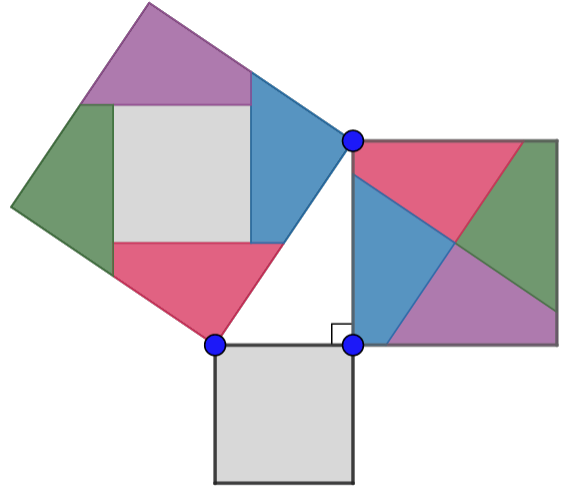
Created with GeoGebra. Author: University of Waterloo. CC BY-NC-SA 4.0. https://ggbm.at/tarGNuVX
This tells us that the area of the large square must be equal to the sum of the areas of the two smaller squares. This important property of right triangles is called the Pythagorean Relationship.
The Pythagorean Relationship
For a right triangle:
The area of the square on the hypotenuse is equal to the sum of the areas of the squares on the other two sides.
Example 1
The areas of the squares on two legs of a right triangle are \(8\) cm2 and \(12\) cm2.
What is the area of the square on the hypotenuse?
Solution
Let's start by letting \(A\) represent the area of the square on the hypotenuse of the right triangle.
By the Pythagorean Relationship, the area of the square on the hypotenuse is equal to the sum of the areas of the squares on the two legs. The result is
\[\begin{align*} A &= 8+12 \\ &= 20 \end{align*}\]
Therefore, the area of the square on the hypotenuse is \(20\) cm2.
Example 2
The square on the hypotenuse of a right triangle has an area of \(34\) cm2.
The square on one leg has an area of \(16\) cm2.
What is the area of the square on the remaining leg of the right triangle?
Solution
Let's start by letting \(A\) represent the area of the square on the remaining leg of the right triangle.
By the Pythagorean Relationship, the area of the square on the hypotenuse is equal to the sum of the areas of the squares on the two legs. The result is
\[34 = A + 16\]
Notice that this time, the unknown area is on the right side of the equation, and so finding the missing area is less straightforward than in our previous example.
But for us, this is not a problem, because we know how to solve for \(A\). We can subtract \(16\) from both sides of the equation.
\[\begin{align*} 34 \class{hl2}{-16} &= A + 16 \class{hl2}{-16} \\ 18 &= A \end{align*}\]
Therefore, the area of the square on the remaining leg is \(18\) cm2.
Check Your Understanding 1
Question — Version 1
The square on the hypotenuse of a right triangle has an area of \(106\) m2. The square on one leg has an area of \(39\) m2. What is the area of the square on the remaining leg of the triangle?
Answer — Version 1
\(67\) m2
Feedback — Version 1
We will start by letting \(A\) represent the area of the square on the remaining leg.
The Pythagorean relationship tell us the area of the square on the hypotenuse is equal to the sum of the areas of the squares on the two legs. So,
\[\begin{align*} 106 &= A + 39 \\ 106 - 39 &= A + 39 - 39 \\ 67 &= A\end{align*}\]
Therefore, the area of the square on the remaining leg is \(67\) m2.
Question — Version 2
The square on one leg of a right triangle has an area of \(18\) cm2. The square on the other leg has an area of \(64\) cm2. What is the area of the square on the hypotenuse of the right triangle?
Answer — Version 2
\(82\) cm2
Feedback — Version 2
We will start by letting \(C\) represent the area of the square on the hypotenuse.
The Pythagorean relationship tell us the area of the square on the hypotenuse is equal to the sum of the areas of the squares on the two legs. So,
\[\begin{align*} C &= 18 + 64 \\ C &= 82 \end{align*}\]
Therefore, the area of the square on the hypotenuse is \(82\) cm2.