Perimeter and Area of Similar Polygons
Perimeter of Similar Polygons
Given a pair of similar polygons, how are their perimeters related? To help answer this question, consider the similar triangles \(ABC\) and \(DEF\).
By inspection, we see that \(\triangle DEF\) is an enlargement of \(\triangle ABC\) with a scale factor of \(2\). The perimeter of each triangle is given by the sum of the side lengths For \(\triangle ABC\), summing the side lengths directly gives a perimeter of \(11\).
\[ \begin{align*} P_{\triangle ABC} &= AB + BC + AC \\ &= 2 + 4 + 5 \\ &= 11 \end{align*}\]
For \(\triangle DEF\), rather than adding the side lengths directly, notice that we can relate each side length to the corresponding side length in \(\triangle ABC\). The multiplicative factors are all the same, \(2\), and can be factored out to give an expression in terms of the perimeter of \(\triangle ABC\).
\[ \begin{align*} P_{\triangle DEF} &= DE + EF + DF \\ &= 2( AB) +2 (BC) +2(AC) \\ &= 2 \left(AB + BC + AC\right)\\ &= 2\left(P_{\triangle ABC}\right)\\ &=2(11)\\ &=22 \end{align*}\]
In doing so, we see that the perimeter of \(\triangle DEF\) is equal to the perimeter of \(\triangle ABC\) multiplied by the scale factor relating the two similar triangles. In fact, this result holds true for any pair of similar polygons.
The perimeter of a polygon is equal to the perimeter of a similar polygon multiplied by the scale factor relating the two polygons.
Check Your Understanding 4
Question — Version 1
Quadrilateral \(ABCD\) is similar to quadrilateral \(EFGH\). Quadrilateral \(ABCD\) has a perimeter of \(75\) units. Given the side lengths in the diagram, what is the perimeter of quadrilateral \(EFGH\) ?
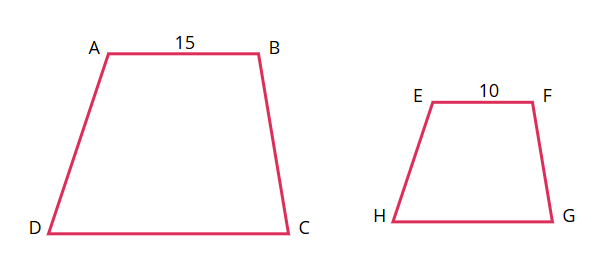
Answer — Version 1
Perimeter of quadrilateral \(EFGH\) is \(50\) units.
Feedback — Version 1
Step 1: Calculate the scale factor
Since the quadrilaterals are similar, the corresponding sides \(AB\) and \(EF\) can be used to determine the scale factor.
\[\begin{align*} EF &= s \cdot AB\\ s &= \dfrac{EF}{AB}\\ &=\dfrac{10}{15}\\ &=\dfrac{2}{3} \end{align*}\]
Step 2: Use the scale factor to determine the perimeter of quadrilateral \(EFGH\).
\[\begin{align*} P_{EFGH} &= s \cdot P_{ABCD}\\ &=\dfrac{2}{3}\cdot 75\\ &=50 \end{align*}\]
Therefore, the perimeter of quadrilateral \(EFGH\) is \(50\) units.
Question — Version 2
Quadrilateral \(ABCD\) is similar to quadrilateral \(EFGH\). Quadrilateral \(ABCD\) has a perimeter of \(32\) units. Given the side lengths in the diagram, what is the perimeter of quadrilateral \(EFGH\) ?
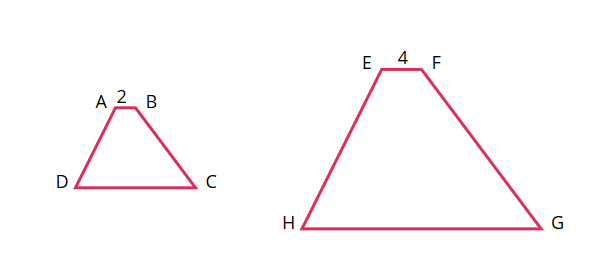
Answer — Version 2
Perimeter of quadrilateral \(EFGH\) is \(64\) units.
Feedback — Version 2
Step 1: Calculate the scale factor
Since the quadrilaterals are similar, the corresponding sides \(AB\) and \(EF\) can be used to determine the scale factor.
\[\begin{align*} EF &= s \cdot AB\\ s &= \dfrac{EF}{AB}\\ &=\dfrac{4}{2}\\ &=2 \end{align*}\]
Step 2: Use the scale factor to determine the perimeter of quadrilateral \(EFGH\).
\[\begin{align*} P_{EFGH} &= s \cdot P_{ABCD}\\ &=2\cdot 32\\ &=64 \end{align*}\]
Therefore, the perimeter of quadrilateral \(EFGH\) is \(64\) units.
Explore This 2
Question
As the scale factor changes, what do you notice about the relationship between the areas of the similar figures?
Description
Triangles
How are the areas of these similar triangles related?
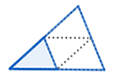
Scale factor: \(2\)
The area of the larger triangle is \(4\) times the area of the smaller triangle.
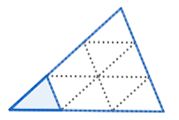
Scale factor: \(3\)
The area of the larger triangle is \(9\) times the area of the smaller triangle.
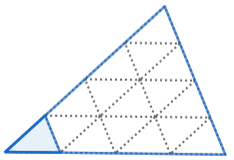
Scale factor: \(4\)
The area of the larger triangle is \(16\) times the area of the smaller triangle.
Parallelograms
How are the areas of these similar parallelograms related?
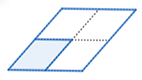
Scale factor: \(2\)
The area of the larger parallelogram is \(4\) times the area of the smaller triangle.
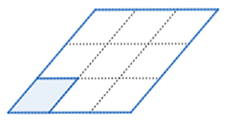
Scale factor: \(3\)
The area of the larger parallelogram is \(9\) times the area of the smaller triangle.
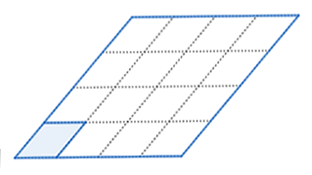
Scale factor: \(4\)
The area of the larger parallelogram is \(16\) times the area of the smaller triangle.
Trapezoids
How are the areas of these similar trapezoids related?
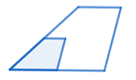
Scale factor: \(2\)
The area of the larger trapezoid is \(4\) times the area of the smaller triangle.
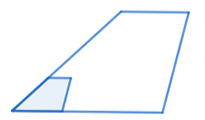
Scale factor: \(3\)
The area of the larger trapezoid is \(9\) times the area of the smaller triangle.
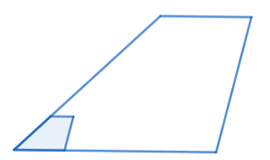
Scale factor: \(4\)
The area of the larger trapezoid is \(16\) times the area of the smaller triangle.
Created with GeoGebra. Author: University of Waterloo. CC BY-NC-SA 4.0.
Interactive Version
https://ggbm.at/zf4mrj54
Explore This 2 Summary
You may have observed that the area of a triangle, parallelogram, or trapezoid is always equal to the area of a similar polygon multiplied by two factors of the relevant scale factor. This makes sense because for each of these polygons, the area involves a product of two lengths.
For example, the area of a parallelogram is equal to its base length multiplied by its height. Consider the area of a parallelogram with a scale factor of \(4\):
\[A_{\text{Parallelogram}} = bh\]
Since the base and height each scale by one factor of the scale factor, the area scales by the square of the scale factor:
\[A_{EFGH}= \left(A_{ABCD}\right)\left(4^2\right) = \left(A_{ABCD}\right)(16)\]
Area of Similar Polygons
Let's explore this result in a bit more detail with a simple but concrete example. Consider two similar rectangles \(ABCD\) and \(EFGH\).
Notice rectangle \(ABCD\) has an area of \(6\),
\[ \begin{align*} A_{ABCD} &= (AB) ( BC) \\ &= 3 ( 2) \\ &= 6 \end{align*}\]
and rectangle \(EFGH\) has an area of \(24\).
\[ \begin{align*} A_{EFGH} &= (EF) ( FG) \\ &= 6 ( 4) \\ &= 24 \end{align*}\]
How are the areas of the similar rectangles related?
The area of a polygon always involves a product of two lengths, in this case, the base times the height.
Therefore, when re-scaling a polygon to create a similar polygon, each length scales by a factor of the scale factor.
This means that their product, the area, will scale by two factors, or the square of the scale factor.
Our example confirms this statement. By inspection, we see that rectangle \(EFGH\) is similar to rectangle \(ABCD\) with a scale factor of \(2\).

\(A_{ABCD}=6\)

\(A_{EFGH}=24\)
Multiplying the area of rectangle \(ABCD\), \(6\), by the square of the scale factor, \(4\), yields the area of rectangle \(EFGH\), \(24\).
\(=\left(A_{ABCD}\right)\left(2^2\right)\)
This result holds for any pair of similar polygons. The area of any polygon is equal to the area of a similar polygon multiplied by the square of the scale factor relating the two polygons.
Let's return now to the problem at the beginning of this lesson.
Try This Revisited
A miniature model of a city has \(3\) square metres of green space. If a length of \(1\) metre on the model corresponds to a length of \(1000\) metres in the real world, then how much green space does the city have?

Source: Miniature City - scanrail/iStock/Getty Images
Solution
The miniature model of the city has the same shape as the city itself. In other words, the miniature model is similar to the actual city. The total area of green space in the real world will therefore be equal to the amount in the model times the square of the relevant scale factor.
\[ A_{\text{Green Space in City}} = \left(A_{\text{Green Space in Model}}\right)\left(s^2\right)\]
We know that \(1\) metre on the model corresponds to \(1000\) metres in the real world. Therefore, the scale factor we need is \(s=1000\).
The total area of green space in the city is therefore equal to the following expression:
\[\begin{align*} A_{\text{Green Space in City}} &= (3) \left(1000^2\right)\\ &= 3~000~000 \end{align*}\]
This is equivalent to \(3\) square kilometres.
Check Your Understanding 5
Question
In the image below, \(\triangle ABC \sim \triangle DEF\). The area of \(\triangle ABC\) is \(81\) square units. Determine the area of \(\triangle DEF\) using the information given.
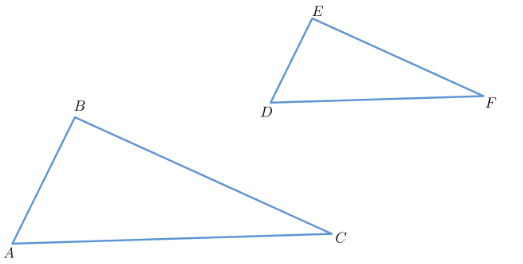
Answer
The area of \(\triangle DEF\) is \(36\) square units.
Feedback
Since the triangles are similar, the corresponding sides \(AB\) and \(DE\) can be used to determine the scale factor.
\[\begin{align*}
s &= \dfrac{DE}{AB}\\
&=\dfrac{6}{9}\\
&=\dfrac{2}{3}
\end{align*}\]
We can now use the scale factor to setermine the area of \(\triangle DEF\).
\[\begin{align*}
A_{\triangle DEF} &= s^2\cdot A_{\triangle ABC}\\
&= \left(\dfrac{2}{3}\right)^2\cdot 81\\
&= \dfrac{4}{9}\cdot 81\\
&=36
\end{align*}\]
Therefore, the area of \(\triangle DEF\) is \(36\) square units.