Alternative Format — Lesson 3: Tangent Ratio

Let's Start Thinking

Introduction

The ancient Romans used aqueducts to transport water over great distances. In order for this to work, the aqueducts had to maintain a very shallow but uniform slope.

Similar problems are faced by builders and engineers today. For example, most trains cannot handle inclines of more than a few degrees.

Aqueduct

Aqueduct.

Source: Aqueduct - Bertl123/iStock/Getty Images

Passenger Train

Passenger train in the mountains.

Source: Passenger Train - Leonid Andronov/iStock/Getty Images

It is critical, then, that we develop a powerful set of tools for tackling these sorts of problems. In this lesson, we define a new quantity, called the tangent ratio, which will aid in solving problems involving triangles. More generally though, it will help us when working with triangles in any context.


Lesson Goals

  • Compute the tangent ratio for an acute angle in a right-angled triangle given the side lengths.
  • Use the tangent ratio to solve for an unknown side length in a right-angled triangle.
  • Use the inverse tangent operation on your calculator to solve for an interior angle in a right-angled triangle.

Try This

A hockey player shoots a puck towards an open net \(5.5\) m away. The net is \(1.2\) m tall. If the puck comes off of the ice, what is the maximum angle that it can make with the ice and still go in the net? (Assume that the puck travels quickly enough that we can ignore the effects of gravity.)

Hockey player 5.5 metres from a 1.2 metre tall net.

Source: Hockey Player - aarrows/iStock/Getty Images


What is the Tangent Ratio?


Slope and Right-Angled Triangles

Right-angle triangles are a useful tool for discussing slopes.

Recall

\[\mathrm{slope} = \frac{\mathrm{rise}}{\mathrm{run}} \]

The angle adjacent to the run and opposite to the rise is called the slope angle.

More generally, we denote an angle of interest with a symbol. The Greek letter \(\theta\) (pronounced theta) is frequently used.

Since the concepts of rise and run tend to be associated with vertical and horizontal distances respectively, it is helpful to generalize these ideas too. We do this by describing the legs of the triangle as either adjacent or opposite to the angle of interest, as illustrated in the diagram. We can abbreviate hypotenuse, opposite, and adjacent to hyp, opp, and adj, respectively.

Recall that adj=run and opp=rise

The Tangent Ratio

Let's now formally define the tangent ratio.

In a right-angled triangle, the tangent of an acute angle is the ratio of the opposite side length to the adjacent side length.

\[\tan(\theta) = \frac{\text{opp}}{\text{adj}}\]

Right triangle with leg opposite angle labelled opp and other leg labelled adj. Hypotenuse is labelled hyp.

Common Practice

  • In equations, note that we will always write "tan" for tangent.
  • We will also often say "tan", instead of "tangent" when referring to the tangent ratio.
  • It is good practice to write brackets around the angle, to prevent confusion with respect to order of operations.

Example 1

Determine \(\tan (\theta)\) for the triangle shown using the definition \(\tan (\theta) = \dfrac{\text{opp}}{\text{adj}}\).

Right triangle ACB, where C is right. AB=13, BC=5, AC=12, angle A=theta.

Solution

With respect to the angle \(\theta\)

  • the opposite side length is equal to \(5\) and
  • the adjacent side length is equal to \(12\).

Therefore, we can determine the tangent ratio, or tan of the angle \(\theta\):

\[ \begin{align*} \tan(\theta) &= \dfrac{\text{opp}}{\text{adj}} \\ \tan (\theta )&= \frac{5}{12} \end{align*}\]

Check Your Understanding 1

Question

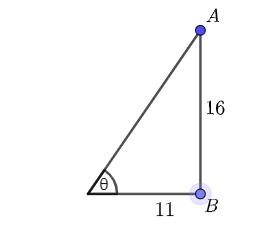
Construct a right triangle with \(\tan(\theta)=\dfrac{\text{opp}}{\text{adj}}=\dfrac{16}{11}\)

Answer

A right triangle with angle theta indicated. The side opposite theta has length 16. The side adjacent to theta has length 11.

Created with GeoGebra. Author: University of Waterloo. CC BY-NC-SA 4.0.

Feedback

One way to construct the desired triangle is to set the side length opposite of \(\theta\) to \(16\) and the side length adjacent to \(\theta\) to \(11\).

Interactive Version

Tangent Ratio

Explore This 1

Question

Modify the lengths of the legs of the given triangle, with values between \(1\) and \(36\), to construct as many triangles as you can with \(\tan(\theta)=\dfrac{\text{opposite}}{\text{adjacent}}=\dfrac{1}{2}\).

Description

We will begin by finding two triangles that fit the criteria. Consider a right triangle with both legs having length \(5\). In this case \(\tan(\theta)=\dfrac{\text{opposite}}{\text{adjacent}}=\dfrac{5}{5}\)

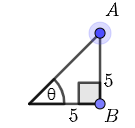
A right triangle with length of both legs equal to 5.

Observe that if we increase the length of the adjacent side to \(10\), then \(\tan(\theta)=\dfrac{5}{10}=\dfrac{1}{2}\).

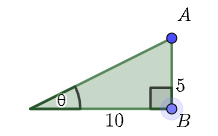
Right triangle with the side opposite theta having length 5, and the side adjacent to theta having length 10.

Now consider increasing the length of the adjacent side to \(12\). Now, \(\tan(\theta)=\dfrac{5}{12}\)

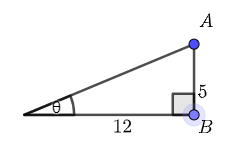
Right triangle with the side opposite theta having length 5, and the side adjacent to theta having length 12.

Observe that if we now increase the length of the opposite side to \(6\), then \(\tan(\theta)=\dfrac{\text{opposite}}{\text{adjacent}}=\dfrac{6}{12}=\dfrac{1}{2}\).

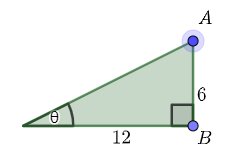
Right triangle with the side opposite theta having length 6, and the side adjacent to theta having length 12.

Created with GeoGebra. Author: University of Waterloo. CC BY-NC-SA 4.0.

Continue your investigation to see how many more triangles fit the criteria.

Interactive Version

Explore the Tangent Ratio in Triangles

Explore This 1 Summary

In this activity, you may have noticed that a tangent ratio of \(\dfrac{1}{2}\) can be achieved in multiple ways. In fact, if it weren't for the size limitation of the question, it could be achieved in infinitely many ways.

Why is this?

The tangent ratio is the rise over the run, so as long as rise and run are in a \(1\) to \(2\) ratio, the tangent ratio simplifies to \(\dfrac{1}{2}\) regardless of the size of the triangle.

Note that \(\tan (\theta )= \dfrac{\text{opp}}{\text{adj}} = \dfrac{1}{2}\) for each triangle:

Right triangle with adjacent=2 and opposite=1.

Right triangle with adjacent=4 and opposite=2.

Right triangle with adjacent=6 and opposite=3.

You may have also observed that all of the triangles with this tangent ratio are similar to one another. One way to see why this is, is to recall that any two similar triangles will have the same shape. This means that corresponding side lengths are in the same proportions. Therefore, any scale factor difference in side lengths between two similar triangles is cancelled out when computing a ratio of two side lengths within one of those triangles.

Example 2

Let's look at an example making use of similarity to compute a tangent ratio.

Determine \(\tan(D)\) given that \(\triangle ABC \sim \triangle EDF\).

Right triangle ABC with AC=8 and BC=6, and C the right angle.

Right triangle EDF, where F is right.

Solution

Given \(\triangle ABC \sim \triangle EDF\), we know that \(\angle B\) and \(\angle D\) are corresponding, and therefore equal. Consequently, their tangent ratios will also be equal.

From the perspective of angle \(B\) in \(\triangle ABC\), the opposite side length is \(8\) while the adjacent side length is \(6\). The ratio of these two values simplifies to \(\dfrac{4}{3}\).

\(\tan(D)\)

\(=\tan(B)\)

 

\(=\dfrac{8}{6}\)

 

\(=\dfrac{4}{3}\)

Therefore, \(\tan(D) = \dfrac{4}{3}\).


Check Your Understanding 2

Question

Determine the exact value of the tangent of \(\theta\).

Two right triangles ABC and ADE, with right angles at B and D respectively. Angles BAC and DAE are opposite angles, and A is the point of intersection of line segments BD and CE.

Answer

\(\tan(\theta)=\dfrac{3}{10}\)

Feedback

Observe, 

\[\begin{align*} \angle BAC=\angle DAE \tag{opposite angles}\\ \angle ABC=\angle ADE \tag{right angles} \end{align*}\]

Therefore, \(\triangle ABC\sim \triangle ADE\) by the angle-angle similarity rule.

Since the two triangles are similar, the tangent ratios for corresponding angles will be the same. We can use this property to solve for the desired tangent ratio noting that \(\angle ACB\) corresponds to \(\angle AED\).

\(\tan(\theta) = \tan(\angle AED) = \tan(\angle ACB) = \dfrac{3}{10}\)


Applications of the Tangent Ratio


Previously, we were tasked with computing the tangent ratio given the side lengths of a triangle. In this part, we will do the reverse. That is, we will use the tangent ratio in combination with other information to determine unknown properties of a triangle.

Example 3

For the triangle shown, \(\tan (\theta) = \dfrac{7}{3}\). Determine the opposite side length with respect to \(\theta\).

Right triangle ABC with angle B=theta, C a right angle, and BC=15. What is AC?

Solution

Recall

The tangent ratio gives us the ratio of the opposite side length to the adjacent side length.

\( \tan (\theta )= \dfrac{\text{opp}}{\text{adj}}\)

We multiply both sides of this relation by the adjacent side length to get an equation for the opposite side length in terms of the tangent ratio and the adjacent side length.

\[\begin{align*} \text{opp} &= \left(\tan(\theta )\right)\left( \text{adj}\right) \\ &= \left(\frac{7}{3} \right)\left( 15\right) \\ &= 35 \end{align*}\]

Therefore, the opposite side has a length of \(35\).


Check Your Understanding 3

Question

For the triangle shown, \(\tan(\theta)=\dfrac{8}{15}\). Determine the length of the hypotenuse.

Triangle ABC has angle ABC = 90 degrees, angle ACB is theta, AB has length 16, and the hypotenuse AC is the desired unknown.

Answer

Length of the hypotenuse is \(34\) units.

Feedback

We are given that the opposite side length is equal to \(16\). So let's begin by using the tangent ratio to solve for the length of the adjacent side.

\[\text{adj}=\dfrac{\text{opp}}{\tan(\theta)}=\dfrac{16}{\frac{8}{15}}=30\]

We can now use the Pythagorean Theorem to determine the length of the hypotenuse.

\[\text{hyp}=\sqrt{30^2+16^2}=34\]

Therefore, the length of the hypotenuse is 34 units.


Computing the Tangent of an Angle

We have seen so far that we can use the tangent ratio to solve for unknown side lengths in a triangle. But, if we don't already know the side lengths, then where does the tangent ratio come from? After all, it is defined as the ratio of the opposite side length to the adjacent side length.

We can actually determine the tangent ratio from an angle directly. For example, we can determine the tangent of \(45^{\circ}\) in the following right angled triangle without knowing the side lengths.

Right-angle triangle ACB with right angle ACB. Theta is angle BAC. AC labelled adj and BC labelled opp. Angle A is 45 degrees.

That's because this triangle must be isosceles. That is, the opposite and adjacent sides have equal length. Therefore, the ratio of the opposite and adjacent side lengths, which defines the tangent of a \(45^{\circ}\) angle, is equal to \(1\).

Note that angle ABC is 45 degrees.

\[ \tan( 45^{\circ}) = \frac{\mathrm{opp}}{\mathrm{adj}} =1\]

Using Your Calculator to Compute the Tangent Ratio

The previous argument relied on the geometrical construction involving very special angles.

What do we do when we are given an arbitrary angle? Can we always work out the tangent ratio from an angle?

Often, there are tricks to deal with other cases, but the simplest solution is to use the tan button on our calculator. On any scientific calculator there is a button labeled tan. This will compute the tangent ratio to a very high precision for any angle.

For example, using our calculator, we can quickly find out that the tangent of a \(40^{\circ}\) angle is approximately \(0.839\). 

\(\texttt{tan(40)=}\)

\(\texttt{0.839099631}\)

Right-angle triangle ACB with angle A=40 degrees and C is right.

In other words, the ratio of the rise to the run, that is the slope, relative to a \(40^{\circ}\) angle in any right-angle triangle is roughly \(0.839\). 

Important: Since we are working with degrees here, we need to make sure that our calculators are in degrees (DEG) mode, opposed to radians (RAD) mode or gradians (GRAD) mode. Changing modes is usually done with the DRG button.

Check Your Understanding 4

Question

Use your calculator to compute \(\tan(24.5^{\circ})\). Round your answer to two decimal places.

Answer

\(\tan(24.5^{\circ})\approx 0.46\)

Feedback

Using our calculator in degrees mode, we find

\(\tan(24.5^{\circ})\approx 0.455726\)

Rounding off to two decimal places gives

\(\tan(24.5^{\circ})\approx 0.46\)

Example 4

A freight train can operate on a maximum incline of \(2^{\circ}\). What is the maximum height that it can climb vertically over a \(10\) km distance?

Solution

The train starts at \(A\) and begins travelling towards \(B\) at an incline of \(2^{\circ}\).

Right triangle ACB with angle A=2 degrees, C is right, AC=10 km, and BC=unknown.

To estimate the maximum height that the train can climb, we assume that the train travels the entire ‌10 km distance at an incline of \(2^{\circ}\). This forms a right-angle triangle whose opposite side length represents the height we are interested in finding.

Right triangle ACB where AC is labelled adj and BC is labelled opp.

Source: Train - ioanmasay/iStock/Getty Images

Recall the tangent ratio is equal to the ratio of the opposite and adjacent side lengths.

Rearranging the definition of the tangent ratio, we obtain an equation for the opposite side length.

\( \tan( \theta )\)

\(= \dfrac{\text{opp}}{\text{adj}}\)

\(\text{opp}\)

\(= \tan(\theta )\cdot \text{adj}\)

Next, we substitute in the adjacent side length of \(10\) km, and use our calculator to evaluate \(\tan(2^{\circ})\):

\[\tan (2^{\circ} )\approx 0.035\]

Now, with a quick calculation, we can determine the maximum vertical distance:

\[\begin{align*} \text{opp} &= \tan( 2^{\circ}) \cdot \mathrm{adj} \\ & \approx 0.035 \cdot (10) \\ &= 0.35 \end{align*}\]

Therefore, the train can climb a maximum vertical distance of \(0.35\) km, or \(350\) m, over a \(10\) km horizontal distance.


Check Your Understanding 5

Question

Carol would like to build a set of steps on a hilly section of her garden. The hill slopes at an angle of \(25.3^{\circ}\) with respect to the flat ground. If each step will be \(18.1\) cm high, what should the depth of each step be, to the nearest tenth? (The depth refers to the distance from the front to the back of one step.) Round answer to one decimal place.

A side view of a step. The top (line segment AC) and front (line segment AB) of the step form the legs of a right triangle ABC. A line from the base of one step to the base of the step above it forms the hypotenuse BC.

Answer

The depth of the step should be \(38.3\) cm.

Feedback

We first compute the tangent ratio of the slope angle. This will give us the ratio of the step height (rise, ,or \(AB\)) to the step depth (run, or \(AC\)).

\[\tan(25.3^{\circ})=0.472\ldots\]

We now use the definition of the tangent ratio to solve for the step depth.

\[\tan(\theta)=\dfrac{\text{opp}}{\text{adj}}\quad\implies\quad\text{adj}=\dfrac{\text{opp}}{\tan(\theta)}=\dfrac{18.1}{0.472\ldots}\approx38.3\]

Therefore, each step should be \(38.3\) cm deep.


The Inverse Tangent Operation


Finding the Angle for a Tangent Ratio

Given an angle, we now know how to convert this into a tangent ratio. How do we reverse this procedure? That is, how do we find the angle corresponding to a particular tangent ratio?

On most scientific calculators, a secondary feature programmed into the tan button is the inverse tangent operation denoted tan-1.

This operation (which is often referred to as taking the inverse tan or tan inverse) will compute the angle corresponding to a tangent ratio to a very high precision.

\[ \theta = \tan^{-1} \left( \frac{\text{opp}}{\text{adj}} \right)\]

For example, using the inverse tangent operation on our calculator, we can quickly determine that the tan inverse of \(\dfrac{2}{3}\) is approximately \(33.7\). Note, we often write brackets around the argument of the inverse tangent operation to indicate the desired order of operations. That is, we first compute opposite divided by adjacent, and then take the inverse tangent of the result.

\(\texttt{tan}^{-1}\texttt{(2}\div \texttt{3)=}\)

\(\texttt{33.69006753}\)

This means that a tangent ratio, or \(\dfrac{\text{rise}}{\text{run}}\), of  \(\dfrac{2}{3}\) corresponds to a slope angle of approximately \(33.7^{\circ}\).

Right triangle ACB with right angle ACB. AC=3, BC=2, angle A=approximately 33.7.

Right triangle DFE with right angle DFE. DF=6, EF=4, angle D=approximately 33.7.

Important: Don't forget to ensure that your calculator is in degrees (DEG) mode.

Check Your Understanding 6

Question

Determine the angle \(\theta\) in degrees in the triangle shown. Round your answer to two decimal places.

A right triangle ABC with right angle at A, and theta is angle C. Side BA is 8 units. Side AC is 9 units.

Answer

Angle \(\theta\) is \(41.63^{\circ}\).

Feedback

Using the inverse tangent operation on our calculator, we can compute the desired angle as follows.

\[\begin{align*} \theta&=\tan^{-1}\left(\dfrac{BA}{AC}\right)\\ &=\tan^{-1}\left(\dfrac{8}{9}\right)\\&=41.6335\ldots \end{align*}\]

Therefore, the angle \(\theta\) is equal to \(28.07^{\circ}\) rounded off to two decimal places.

Try This Revisited

A hockey player shoots a puck towards an open net \(5.5\) m away. The net is \(1.2\) m tall. If the puck comes off of the ice, what is the maximum angle that it can make with the ice and still go in the net? (Assume that the puck travels quickly enough that we can ignore the effects of gravity.)

Hockey player a distance of 5.5 metres from a 1.2 metre tall net.

Solution

Let \(\theta\) denote the maximum angle that the puck can make with the ice. This would occur if the puck enters the goal at the top of the net. The path of the puck, the ice, and the net form a right-angled triangle. In this triangle, and from the point of view of the angle theta, the height of the net represents the opposite side length. And the distance from the player to the net represents the adjacent side length.

The ratio gives the tangent of the angle theta:

\[ \tan (\theta) = \frac{1.2}{5.5} \]

 

Right triangle with angle theta between 5.5 metre leg and hypotenuse.

Source: Hockey Player - aarrows/iStock/Getty Images

Using the inverse tangent operation on our calculator, we can solve directly for \(\theta\):

\[\begin{align*} \theta &= \tan^{-1} \left(\frac{1.2}{5.5} \right)\\ &\approx 12.3^{\circ} \end{align*}\]

Therefore, the maximum angle that the puck can make with the ice is roughly \(12.3^{\circ}\).

Check Your Understanding 7

Question

An airplane coming in for landing begins at an altitude of \(2000\) m. The plane touches down a few minutes later \(3200\) m away as measured at ground level. Assuming the plane follows a straight path to the runway, what angle does this path make with the runway? Round your answer to 1 decimal place.

Answer

The plane's path makes an angle of \(32.0^{\circ}\) with the runway.

Feedback

Let \(\theta\) denote the angle that the plane makes with the runway.

A right triangle ABC has right angle A, ,and theta is angle C. Side BA is 2000 metres. Side AC is 3200 metres and is horizontal. An airplane is at point B directly above point A.

Source: plane subjob/iStock/Getty Images Plus

We can use the inverse tangent operation on the ratio of the initial altitude to the horizontal distance covered to find \(\theta\).

\[\begin{align*} \theta&=\tan^{-1}\left(\dfrac{BA}{AC}\right)\\ &=\tan^{-1}\left(\dfrac{2000}{3200}\right)\\ &=32.005\ldots \end{align*}\]

Therefore, the plane makes an angle of approximately \(32.0^{\circ}\) with the horizontal. 


Wrap-Up


Lesson Summary

In this lesson, we learned the following:

  • The tangent ratio for an acute angle in a right-angled triangle is given by the ratio of the opposite and adjacent side lengths:
\[\tan( \theta) = \frac{\mathrm{opp}}{\mathrm{adj}}\]
  • The tangent ratio can be used to solve for unknown side lengths of a right-angled triangle.
  • Given an angle, we can use the tangent operation (i.e., the tan button) on our calculators to find the corresponding tangent ratio.
  • Given a tangent ratio, we can use the inverse tangent operation (i.e., the tan-1 button) on our calculators to find the corresponding angle.

Take It With You

Using your calculator, evaluate each of the following:

  1. \(\displaystyle \tan (0^{\circ})\)
  2. \(\displaystyle \tan( 90^{\circ})\)

Right triangle with angle labelled theta, opposite side from theta labelled opp, other leg labelled adj, and hypotenuse labelled hyp.

Using the definition of the tangent ratio, can you make sense of these values?