The Sine Ratio
Let's begin by formally defining the sine ratio.
In a right-angled triangle, the sine of an acute angle is the ratio of the length of the opposite side to the length of the hypotenuse.
\(\sin(\theta) = \dfrac{\text{opp}}{\text{hyp}}\)
Note that in equations, we will always write sine without the "e". But we will still say "sine":
\(\sin (\theta )= \) sine of theta.
Observe that this definition is very similar to the definition of the tangent ratio, \( \tan(\theta) = \dfrac{\mathrm{opp}}{\mathrm{adj}}\). The difference here is that we use the hypotenuse instead of the adjacent side in the denominator.
The Cosine Ratio
The cosine ratio is also defined in a similar way to the tangent ratio.
In a right-angled triangle, the cosine of an acute angle is the ratio of the length of the adjacent side to the length of the hypotenuse.
\(\cos(\theta) = \dfrac{\text{adj}}{\text{hyp}}\)
For the sake of brevity, we will write cosine using the short form "cos". In speech, we may say the full word,, or we may just sound out the short form "cos".
\(\cos (\theta) = \) cosine of theta.
Comparing this to the definitions of the tangent and sine ratios, we notice that each ratio involves a different pair of sides. This suggests that we will choose to make use of different ratios depending on what information is immediately available to us in a given problem.
Example 1
Determine \(\sin (\theta) = \dfrac{\mathrm{opp}}{\mathrm{hyp}}\) and \(\cos (\theta) = \dfrac{\text{adj}}{\text{hyp}}\) for the right-angled triangle shown.

Solution
With respect to the angle \(\theta\):
- the opposite side length is equal to \(21\) and
- the adjacent side length is equal to \(20\).
We can use the Pythagorean Theorem to calculate the length of the hypotenuse.

We can now calculate the sine and cosine ratios using their definitions. We find:
\(\sin(\theta) = \dfrac{21}{29}\)
\(\cos(\theta) = \dfrac{20}{29}\)
Explore This 1
Description
Modify the legs of the given triangle, with values between \(1\) and \(20\), to construct as many right triangles as you can with \(\sin(\theta)=\dfrac{\text{opp}}{\text{hyp}}=\dfrac{3}{5}\). What is the value of \(\cos(\theta)=\dfrac{\text{adj}}{\text{hyp}}\) for these triangles?
We will begin by finding two triangles that fit the criteria. Consider a right triangle with both legs having length \(4\). In this case \(\sin(\theta)=\dfrac{\text{opp}}{\text{hyp}}=\dfrac{4}{\sqrt{32}}\).
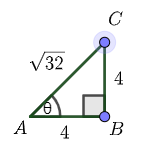
Observe that if we decrease the length of the opposite side to \(3\), then \(\sin(\theta)=\dfrac{3}{5}\).
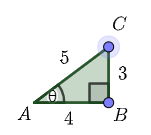
For this triangle, \(\cos(\theta)=\dfrac{4}{5}\).
Now consider increasing the length of the adjacent side to \(8\). Now, \(\sin(\theta)=\dfrac{3}{\sqrt{73}}\).
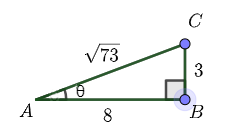
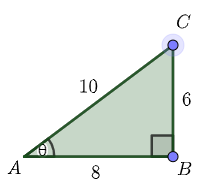
Observe that if we now increase the length of the opposite side to \(6\), then \(\sin(\theta)=\dfrac{6}{10}=\dfrac{3}{5}\).
Created with GeoGebra. Author: University of Waterloo. CC BY-NC-SA 4.0.
For this triangle, \(\cos(\theta)=\dfrac{8}{10}=\dfrac{4}{5}\).
Continue your investigation, to see how many more triangles fit the criteria of \(\sin(\theta)=\dfrac{3}{5}\). Remember to note the value of \(cos(\theta)\) for each triangle.
Interactive Version
Sine Ratio
Explore This 1 Summary
In the activity, you should have found that a sine ratio of 3 over 5 can be achieved in multiple ways. This is because a sine ratio only determines the shape of a triangle. It is not affected by the scale.
Recall the same was true of the tangent ratio. You may have also noticed that whenever the sine ratio was equal to 3 over 5, the cosine ratio was equal to 4 over 5. This is because a sine ratio of 3 over 5 specifies the same shape as a cosine ratio of 4 over 5, and vise versa. In particular, they both describe a triangle with side lengths in a 3 to 4 to 5 ratio.
Finally, you may have observed that all of the triangles with a particular sine or cosine ratio are similar. This goes back to the idea that the sine or cosine ratio only determines the shape, and any two triangles with the same shape are, by definition, similar.
Trigonometry
Trigonometry, which comes from Greek words for triangle and measure, is the study of relationships involving the side lengths and angles of triangles.
Early mathematicians noticed something interesting specifically about right angle triangles. In a right-angled triangle, if one angle other than the right angle is known, then the third angle is determined by the fact that the sum of the three angles must be 180 degrees, and the shape of the triangle is fixed. An additional knowledge of one side length fixes the scale and determines the other two side lengths.

The trigonometric ratios sine, cosine, and tangent relate side lengths and angles of triangles, making them essential tools in trigonometry.
\(\cos(\theta) = \dfrac{\text{adj}}{\text{hyp}}\)
\(\tan(\theta) = \dfrac{\text{opp}}{\text{adj}}\)
The SOH-CAH-TOA Mnemonic
Each trigonometric ratio is defined as a quotient of two side lengths in a right-angled triangle.
\[\sin( \theta) = \frac{\mathrm{opp}}{\mathrm{hyp}} \qquad \cos (\theta) = \frac{\mathrm{adj}}{\mathrm{hyp}} \qquad \tan( \theta )= \frac{\mathrm{opp}}{\mathrm{adj}} \qquad \]
These definitions, especially being so similar, can be tricky to remember. To help remember these definitions, it is common to form the mnemonic SOH-CAH-TOA. Each letter represents the first letter of each object in each equation, in the order in which they appear.
Consider the following example:
\[ \mathrm{SOH} \qquad \rightarrow \qquad \sin (\theta) = \frac{\mathrm{opp}}{\mathrm{hyp}} \]
Here, the S represents sine of theta, the O stands for opposite, and H stands for hypotenuse. Putting this together in the form of a trigonometric ratio gives sine of theta equals opposite over hypotenuse.