Properties and Laws of Logarithms Alternative Format

Lesson Part 1

Introduction

When working with exponents, we employ a variety of properties and laws to help simplify and evaluate exponential expressions, some of which are shown here.

Properties	Laws/Rules
\(c^0 = 1, ~c \neq 0\)	Product of Powers: \((c^m)(c^n)=c^{m+n}\)
\(c^{-n} = \dfrac{1}{c^n}\)	Quotient of Powers: \(\dfrac{c^m}{c^n} = c^{m-n}\)
\(c^{\frac{1}{n}} = \sqrt[n]{c}\)	A Power of a Power: \((c^m)^n = c^{mn}\)

Logarithms have similar properties and laws which we will discuss in this module and apply to simplify logarithmic expressions and solve simple exponential and logarithmic equations.

We will first define a common logarithm.

Common Logarithms

A logarithm base \(10\) is called a common logarithm. For simplicity, \(\log_{10}(x)\) is often written \(\log(x)\), with base \(10\) understood.

Common logarithms were the first logarithms introduced to carry out complicated calculations in the decimal number system (base \(10\)).

The log function log on your calculator works in base \(10\).

Examples

Example 1

Evaluate.

a. \(\log (0.001)\)

b. \(\log(70)\)

c. \(\log (-100)\)

Solution

a. It sometimes helps to express the logarithm with the base 10 to clarify your thought process. However, it is not necessary to do this.

Evaluating this logarithm, we have

\[ \begin{align*} \log_{10}{(0.001)} &=\log_{10}{\left(\dfrac{1}{1000}\right)} \\ &=\log_{10}{(10^{-3})} \\ &=-3 \end{align*} \]

You can also use the log function on your calculator log. This works in base \(10\) (common base).

Confirm this answer with your calculator, then use your calculator to evaluate \(\log(70)\) and \(\log(-100)\).

b. \(\log(70) = 1.84509804 \ldots\)

Since this answer is the value of an exponent, it is important to keep \(3\) or \(4\) decimal places in your answer when rounding.

Therefore, \(\log (70) \approx 1.845\). This means that \(10^{1.845} \approx 70\).

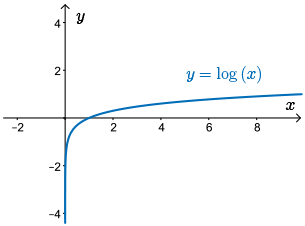
c.The calculator returns an error when asked to determine \(\log (-100)\).

Why is this?

If we let \(\log (-100)= n\), then \(10^n = -100\).

There is no value for \(n\) such that \(10^n\) produces a negative value since the base is positive.

Also, remember that the domain of the logarithmic function \(y = \log_{c}(x), c \gt 0,~ c \neq 1\) is \(\left\{ x \mid x \gt 0, x \in \mathbb{R} \right\}\).

The graph of \(y = \log_{10}(x)\) shown here supports the fact that the \(\log(-100)\) does not exist.

Example 2

The next set of questions involve logarithms within an exponential expression. Evaluate each, then use your answers to a) and b) to predict an answer for c).

a) \(4^{\log_{4}{(64)}}\)

b) \(5^{\log_{5} {\left(\frac{1}{25}\right)}}\)

c) \(3^{\log_{3}{(20)}}\)

Solution

When evaluating the answer for a) and b), we begin with the value of the exponent.

a) We have

\[ \begin{align*} 4^{\color{BrickRed}{\log_{4}(64)}} &=4^{\color{BrickRed}3} \\ &=64 \end{align*} \]

b) We have

\[ \begin{align*} 5^{\color{BrickRed}{\log_{5} \left(\frac{1}{25} \right)}} &=5^{\color{BrickRed}{-2}} \\ &=\dfrac{1}{25} \end{align*} \]

Notice \(4^{\log_{4}{\color{NavyBlue}(64)}} = {\color{NavyBlue}64}\) and \(5^{\log_{5}{ {\color{NavyBlue} \left( \frac{1}{25} \right)}}} = {\color{NavyBlue}{\dfrac{1}{25}}}\). It would seem that \(3^{\log_{3}(20)}\) should equal \(20\).

c) If we let \({\color{BrickRed}3}^{\color{Mulberry}{\log_{3}(20)}} = {\color{NavyBlue}n}\) and convert to logarithmic form, we have

\[ \begin{align*} \log_{\color{BrickRed}{3}}{\color{NavyBlue}(n)} &= {\color{Mulberry}{\log_{3}(20)}} \\ \therefore n &= 20 \end{align*} \]

This property of logarithms follows from the exponent property, where two powers of the same base are equal if and only if their exponents are equal.

Thus,

\[3^{\log_{3}(20)} = 20\]

In general, \(c^{\log_{c}(n)} = n\) for all \(c \gt 0,~ c \neq 1, ~n \gt 0\).
Similarly, \(\log_{c}(c^n) = n\) for all \(c \gt 0,~ c \neq 1,~ n \in \mathbb{R}\).

Remember, a logarithm will reverse or undo the operation of exponentiation, much like multiplication will undo division. This is simply what is happening within each of these statements.

Lesson Part 2

Examples

In this next example, we are asked to solve for \(x\) in simple equations involving logarithms. Try solving each of these equations using the equivalent exponential form.

Example 3

Solve for \(x\).

a. \(\log_{16} \left( \sqrt{8} \right)= x \qquad\qquad\)

b. \(\log_{x}\left(15\right)= 2 \qquad\qquad\)

c. \(\log_{4}\left(x\right)= 0\)

Solve each of these equations using the equivalent exponential form:

\[\log_{\color{BrickRed}c}({\color{NavyBlue}m})= {\color{Mulberry}n} \Longleftrightarrow {\color{NavyBlue}m}={\color{BrickRed}c}^{\color{Mulberry}n}~\text{when}~{\color{BrickRed}c} \gt 0, {\color{BrickRed}c} \neq 1, {\color{NavyBlue}m} \gt 0\]

Solution

a. We solve the equivalent exponential equation by finding a common base and equating the bases.

\[ \begin{align*} \log_{\textcolor{BrickRed}{16}}\left( \textcolor{NavyBlue}{\sqrt{8}} \right)= \textcolor{Mulberry}{x} \quad \implies \quad \textcolor{BrickRed}{16}^{\textcolor{Mulberry}{x}} &=\textcolor{NavyBlue}{8^{\frac{1}{2}}} \\ (2^4)^x &= (2^3)^{\frac{1}{2}} \\ 4x &= \dfrac{3}{2} \\ \therefore x &= \dfrac{3}{8} \end{align*} \]

b. The equivalent exponential form is a quadratic equation.

\[ \log_{\textcolor{BrickRed}{x}}(\textcolor{NavyBlue}{15})= \textcolor{Mulberry}{2} \quad \implies \quad \textcolor{BrickRed}{x}^{\textcolor{Mulberry}{2}}=\textcolor{NavyBlue}{15} \]\[ x = \pm \sqrt{15} \]

But, the base of the logarithmic expression must be positive. Therefore, \(x \gt 0\).

\[ \therefore x = \sqrt{15} \]

c.

\[ \begin{align*} \log_{\textcolor{BrickRed}{4}}(\textcolor{NavyBlue}{x})= \textcolor{Mulberry}{0} \quad \implies \quad \textcolor{BrickRed}{4}^{\textcolor{Mulberry}{0}} &=\textcolor{NavyBlue}{x} \\ \therefore x &= 1 \end{align*} \]

Note:

\(\log_{c}(1)=0\), for all \(c \gt 0\), \(c\neq 1\). This follows from the exponential property \(c^0 = 1\), \(c \neq 0\).

Check Your Understanding A, B, and C

These questions are not included in the Alternative Format, but can be accessed in the Review section of the side navigation.

Example 4

Solve \(\log_{9}(\log_{8}(x-3)) = -\dfrac{1}{2}\).

Solution

This equation involves a logarithm within a logarithm.

First note the restrictions on \(x\) since the argument of a logarithm must be positive.

Thus, \(x \gt 4\).

Most logarithmic equations can be solved using the equivalent exponential form. We begin with the conversion

\[ \begin{align*} \log_{\color{BrickRed}9}({\color{NavyBlue}{\log_{8}(x-3)}}) = -{\color{Mulberry}{\dfrac{1}{2}}} \quad \implies \quad {\color{BrickRed}9}^{\color{Mulberry}{-\frac{1}{2}}} &= {\color{NavyBlue}{\log_{8}(x-3)}} \\ \dfrac{1}{3} &= \log_{8}(x-3) \end{align*} \]

We now convert this statement to exponential form.

\[ \begin{align*} \log_{\textcolor{BrickRed}{8}}{\color{NavyBlue}(x-3)} = {\color{Mulberry}{\dfrac{1}{3}}} \quad \implies \quad {\color{BrickRed}8}^{\color{Mulberry}{\frac{1}{3}}} &={\color{NavyBlue}{x - 3}} \\ 2 &= x-3 \\ x &= 5 \end{align*} \]

Therefore, \(x = 5\), which satisfies the condition \(x \gt 4\).

Example 5

Solve \(8^{\log_{4}(x+1)} = 27\).

Solution

The equation in this example has a logarithmic expression within an exponential equation.

First note restrictions on \(x\); since \(x+1 \gt 0\), then \(x \gt -1\).

We cannot solve this exponential equation by finding common bases since we cannot express \(8\) and \(27\) with the same base. We can, however, simplify the left side of the equation.

We know \(c^{\log_{c}(n)} = n\), \(n \gt 0\), but the bases must be the same.

The logarithm is base \(4\) and we can express \(8\) as a power base \(4\); that is, \(8 = 4^{\frac{3}{2}}\).

\[ \begin{align*} 8^{\log_{4}(x+1)} &=27 \\ \left(4^{\color{BrickRed}{\frac{3}{2}}}\right)^{\color{NavyBlue}{\log_{4}(x+1)}} &= 27 \\ \left(4^{\color{NavyBlue}{\log_{4}(x+1)}}\right)^{\color{BrickRed}{\frac{3}{2}}} &=27 \quad \text{since}~(x^a)^b = (x^b)^a = x^{ab} \end{align*} \]

Using the property \(c^{\log_{c}(n)} = n\), \(n \gt 0\), we know \(4^{\log_{4}(x+1)}= x + 1\).

So our equation simplifies to

\[ \begin{align*} (x+1)^{\frac{3}{2}} &= 27 \\ \left( (x+1)^{\frac{3}{2}} \right)^{\frac{2}{3}} &= 27^{\frac{2}{3}} \\ x+1 &= \left(\sqrt[3]{27}\right)^2 \\ x+1 &= 9 \\ x &= 8 \quad \text{which satisfies}~x \gt -1 \end{align*} \]

Therefore, \(x=8\).

Keep in mind that raising both sides of an equation to an even exponent may produce extra incorrect results. However, in this situation, squaring both sides of the equation resulted in a correct solution. Identifying the restrictions on the variable in the original equation will help in identifying any extraneous roots.

Check Your Understanding D

This question is not included in the Alternative Format, but can be accessed in the Review section of the side navigation.

Lesson Part 3

Laws of Logarithms

Logarithm of a Product

Product Law

 

\[\log_{c}(xy) = \log_{c}(x) + \log_{c}(y),~\text{where}~c \gt 0, c \neq 1, x \gt 0, y \gt 0\]

This is the logarithmic form of the exponent law \((c^m)(c^n) = c^{m+n}\).

Proof:

Let \(\log_{c}(x) = m\) and \(\log_{c}(y) = n\).

Then, \(c^m = x\) and \(c^n = y\).

Now,

\[ \begin{align*} \log_{c}(xy) &=\log_{c}(\textcolor{BrickRed}{c^m \cdot c^n}) &\text{since}~x=c^m~\text{and}~y=c^n \\ &= \log_{c}(\textcolor{BrickRed}{c^{m+n}}) \\ &= m + n &\text{but}~m = \log_{c}(x)~\text{and}~n = \log_{c}(y) \\ &=\log_{c}(x) + \log_{c}(y) \end{align*} \]

\(\therefore \log_{c}(xy) = \log_{c}(x) + \log_{c}(y)\), as required.

Logarithm of a Quotient

Quotient Law

 

\[\log_{c}{\left( \dfrac{x}{y} \right)} = \log_{c}(x) - \log_{c}(y),~\text{where}~c \gt 0, c \neq 1, x \gt 0, y \gt 0\]

This is the logarithmic form of the exponent law \(\dfrac{c^m}{c^n} = c^{m-n}\).

Proof:

Let \(\log_{c}(x)= m\) and \(\log_{c}(y) = n\).

Rewriting each in exponential form gives \(c^m = x\) and \(c^n = y\).

Now,

\[ \begin{align*} \log_{c}\left(\dfrac{x}{y}\right) &= \log_{c}\left(\textcolor{BrickRed}{\dfrac{c^m}{c^n}}\right) \\ &= \log_{c}(\textcolor{BrickRed}{c^{m-n}}) \\ &= m - n &\text{but}~m = \log_{c}(x) \text{and}~n = \log_{c}(y) \\ &=\log_{c}(x) - \log_{c}(y) \end{align*} \]

\(\therefore \log_{c}\left(\dfrac{x}{y}\right) = \log_{c}(x) - \log_{c}(y)\), as required.

We can see in this proof that we are applying the corresponding exponential law for the quotient of powers.

Logarithm of a Power

Power Law

\[\log_{c}(x^n) = n\log_{c}(x),~\text{where}~c \gt 0, c \neq 1, x \gt 0\]

This is the logarithmic form of the exponent law \((c^m)^n = c^{mn}\).

Proof:

Let \(\log_{c}(x) = m\). Then, \(c^m = x\).

Now,

\[ \begin{align*} \log_{c}(x^n) &= \log_{c}\left (\textcolor{BrickRed}{(c^m)^n}\right) &\text{since}~x=c^m~\text{and}~y=c^n \\ &= \log_{c}(\textcolor{BrickRed}{c^{mn}}) \\ &= mn &\text{but}~m = \log_{c}(x) \\ &=n\log_{c}(x) \end{align*} \]

\(\therefore \log_{c}(x^n) = n\log_{c}(x)\), as required.

Lesson Part 4

Examples

Let's work through some examples involving these laws.

Example 6

Simplify each expression to a single logarithm.

a. \(\log_{3}(x) + \log_{3}(x-1) - \log_{3}(2x)\)

b. \(\log (2p) - 2\log (q) + 3\log (pq)\)

Solution

a. We apply the product and quotient laws for the sum and difference of the logarithms. We can then simplify the argument here by cancelling a factor of \(x\) from the numerator and denominator.

\[ \begin{align*} \log_{3}(x) + \log_{3}(x-1) - \log_{3}(2x) &=\log_{3}\Big ( x(x-1)\Big)-\log_{3}(2x) \\ &= \log_{3}{\left( \dfrac{x(x-1)}{2x} \right)} \\ &= \log_{3}{\left( \dfrac{x-1}{2} \right)} \end{align*} \]

Note that \(x\gt 1\) to ensure the argument of each logarithm is positive.

b. We must first apply the power law to the second and third exponents, bringing the coefficient in front of the log up as the exponent. We can now express the three logarithms as a single logarithm using the product and quotient law. We then simplify using exponent laws.

\[ \begin{align*} \log (2p) - 2\log (q) + 3\log (pq) &=\log (2p) - \log \left(q^2\right) + \log \left ( (pq)^3\right) \\ &=\log_{}\left(\dfrac{2p}{q^2}\right)+\log_{} \left ( p^3q^3\right) \\ &=\log_{}{\left( \dfrac{2p}{q^2}(p^{3}q^{3}) \right)} \\ &=\log (2p^{4}q) \end{align*} \]

Note that \(p\gt 0\) and \(q\gt 0\) to ensure that the arguments of the logarithms in the original statement are positive.

Check Your Understanding E

This question is not included in the Alternative Format, but can be accessed in the Review section of the side navigation.

Example 7

Express \(\log_{2}{\left(\dfrac{4x^2}{\sqrt{y}}\right)}\) in terms of \(\log_{2}(x)\) and \(\log_{2}(y)\).

Solution

In this example, we will use the laws of logarithms to break up a single logarithm into the components \(\log_{2}(x)\) and \(\log_{2}(y)\).

Note: To express \(\log_{2} \left ( \dfrac{4x^2}{\sqrt{y}}\right)\) in terms of \(\log_{2}(x)\) and \(\log_{2}(y)\), implies \(x\gt 0\) and \(y\gt 0\).

Restrictions on the variables for \(\log_{2} \left ( \dfrac{4x^2}{\sqrt{y}}\right)\) are \(y\gt 0\) and \(x\neq 0\).

Restrictions on the variables for \(2+2\log_{2}(x)-\dfrac{1}{2}\log_{2}(y)\) are \(x\gt 0\) and \(y \gt 0\).

In order to apply the power law to express \(\log_{2}(x^2)\) as \(2\log_{2}(x)\), \(x\), the base of the power, must be greater than zero.

This is important to keep in mind when applying the power law.

Check Your Understanding F

This question is not included in the Alternative Format, but can be accessed in the Review section of the side navigation.

Example 8

Simplify and evaluate \(2\log_{3}(12) - \log_{3}(6) - 3\log_{3}(2)\).

Solution

Check Your Understanding G

This question is not included in the Alternative Format, but can be accessed in the Review section of the side navigation.

Lesson Part 5

Examples

Example 9

Use logarithms to solve \(5^x = 30\).

Solution

\(30\) cannot be easily expressed as a power of \(5\), so we would not solve this exponential equation using common bases.

Earlier in this unit, we used a systematic trial and error method to determine the value of the exponent in this situation.

Method 1:
We can now solve this exponential equation using the power law of logarithms.

\[5^x =30 \]

The first step is to take the logarithm base \(10\) of each side of the equation.

\[ \log (5^x) =\log (30) \]

Then, using the power rule for logarithms, we can bring the exponent down in front of the logarithm and multiply.

\[ x\log (5) =\log (30) \]

Isolating \(x\), we obtain an exact value for \(x\).

\[ x =\dfrac{\log (30)}{\log (5)} \]

Using the calculator, we can obtain an approximate value for the exponent.

\[x \approx 2.113\]

To verify this answer, we can check or show that \(5^{2.113} = 29.98635...\)

We worked base \(10\) to allow us to use the common \(\log\) function on the calculator. However, any base would work here.

---

Method 2:

Another exact solution to \(5^x = 30\) can be found by re-expressing this exponential equations in logarithmic form.

Thus,

\[x = \log_{5}(30)\]

We can also conclude that

\[\log_{5}(30) = \dfrac{\log (30)}{\log (5)},\]

the solution obtained in our first approach.

This leads directly to the change of base formula, used to convert a logarithm to a logarithm with a different base.

Laws of Logarithms

Change of Base Formula

\[\log_{c}(x) = \dfrac{\log_{a}(x)}{\log_{a}(c)},~\text{where}~a~\text{and}~c \gt 0, a~\text{and}~c \neq 1, x \gt 0\]

Proof:

We will consider a proof to this formula.

Let \(\log_{c}(x) = n\), so

\[c^n = x\]

Then we can take the \(\log_a\) of each side of this exponential statement.

\[\log_{a}(c^n) = \log_{a}(x)\]

Then we can apply the power rule for logarithms.

\[\log_{a}(c^n) = \log_{a}(x)\]

The exponent \(n\) can be brought down in front as a coefficient.

\[n\log_{a}(c) = \log_{a}(x)\]

Dividing both sides by \(\log_a(c)\), we have

\[n = \dfrac{\log_{a}(x)}{\log_{a}(c)}\]

But \(n = \log_{c}(x)\)

\[\log_{c}(x) = \dfrac{\log_{a}(x)}{\log_{a}(c)} \]

This formula allows us to convert any logarithm to a different base. For example, \(\log_{3}(20)\) can be calculated using the common log function log on the calculator by converting the base \(3\) logarithm to base \(10\).

\[\log_{3}(20) = \dfrac{\log (20)}{\log (3)}\]

Therefore, \(\log_{3}(20) \approx 2.7268\).

Check Your Understanding H

This question is not included in the Alternative Format, but can be accessed in the Review section of the side navigation.

An Observation

In the previous module, Logarithmic Functions, we determined graphically that \(\log_{\frac{1}{2}}(x) = -\log_{2}(x)\), since the graph of \(y = \log_{\frac{1}{2}}(x)\) is a reflection of \(y = \log_{2}(x)\) in the \(x\)-axis.

Lesson Part 6

Laws of Logarithms

Challenge Problem

If \(\log_{2}(x), 1 + \log_{4}(x)\), and \(\log_{8}(4x)\) are consecutive terms of a geometric sequence, determine the possible values of \(x\).

Note:
A geometric sequence is a sequence of the form \(a\), \(ar\), \(ar^2\), \(ar^3\), \(\ldots\) , \(ar^{n-1}\), \(\ldots\) where the ratio of any term to the preceding term is constant \(\left( \dfrac{t_{n+1}}{t_n} = r,~ r \neq 0, ~n \geq 1, ~n \in \mathbb{Z} \right), ~a\neq 0\).

Solution

Since \(\log_{2}(x), 1 + \log_{4}(x)\), and \(\log_{8}(4x)\) are consecutive terms of a geometric sequence, then

\[\dfrac{1 + \log_{4}(x)}{\log_{2}(x)} = \dfrac{\log_{8}(4x)}{1 + \log_{4}(x)}\]

Now, the arguments of these logarithmic expressions must be positive. So, \(x \gt 0\) and \(4x \gt 0\), and thus \(x \gt 0\).

Also, the denominators of these ratios \(\log_{2}{(x)} \neq 0\) and \(1+\log_{4}{(x)} \neq 0\). Therefore, \(x \neq 1\) or \(\frac{1}{4}\).

To solve this equation, we will convert \(\log_{4}(x)\) and \(\log_{8}(4x)\) to base \(2\) logarithms to work with a common base.

\[\dfrac{1 + \log_{4}(x)}{\log_{2}(x)} = \dfrac{\log_{8}(4x)}{1 + \log_{4}(x)}\]

Using the change of base formula, we can express

\[\log_{4}(x) = \dfrac{\log_{2}(x)}{\log_{2}(4)} = \dfrac{\log_{2}(x)}{2} = \dfrac{1}{2} \log_{2}(x)\]\[\log_{8}(4x) = \dfrac{\log_{2}(4x)}{\log_{2}(8)} = \dfrac{\log_{2}(4x)}{3} = \dfrac{\log_{2}(4) + \log_{2}(x)}{3} = \dfrac{2}{3} + \dfrac{1}{3}\log_{2}{(x)}\]

So we must solve

\[ \begin{align*} \dfrac{1 + \frac{1}{2}\log_{2}(x)}{\log_{2}(x)} &= \dfrac{\frac{2}{3} + \frac{1}{3}\log_{2}(x)}{1+\frac{1}{2}\log_{2}(x)} \\ \dfrac{1 + \frac{1}{2}\log_{2}(x)}{\log_{2}(x)} &= \dfrac{\frac{2}{3} + \frac{1}{3}\log_{2}(x)}{1+\frac{1}{2}\log_{2}(x)} \end{align*} \]

To simplify the look of the equation, let \(a=\log_{2}(x)\) and solve for \(a\).

\[ \dfrac{1+\frac{1}{2}a}{a} = \dfrac{\frac{2}{3} + \frac{1}{3}a}{1+\frac{1}{2}a} \]

To simplify further, we will multiply both numerator and denominator on the left side of equation by \(2\) to eliminate fractions in this expression. And on the right side, we will multiply numerator and denominator by \(6\) to eliminate the fractions in this expression.

\[ \begin{align*} \dfrac{2\left(1+\frac{1}{2}a\right)}{2a} &= \dfrac{6\left(\frac{2}{3}+\frac{1}{3}a\right)}{6\left(1+\frac{1}{2}a\right)} \\ \dfrac{2+a}{2a} &= \dfrac{4+2a}{6+3a} \end{align*} \]

We now solve a much simpler equation, which results in a quadratic equation that can be factored.

\[ \begin{align*} (2+a)(6+3a) &= 2a(4+2a) \\ 12 + 12a + 3a^2 &= 8a+4a^2 \\ a^2 - 4a - 12 &= 0 \\ (a-6)(a+2) &=0 \end{align*} \]

So \(a=6,-2\).

Since \(a = \log_{2}(x)\),

\[ \begin{align*} \log_{2}(x) & =6 \quad\quad \text{or} & \log_{2}(x) & =-2 \\ x & =2^6 & x & =2^{-2} \\ x & =64 & x & =\dfrac{1}{4} \end{align*} \]

But only \(x = 64\) satisfies the restriction \(x \gt 0,\) \(x \neq 1\), \(\dfrac{1}{4}\).

Therefore, the three terms, \(\log_{2}(x)\), \(1 + \log_{4}{(x)}\), and \(\log_{8}(4x)\), form a geometric sequence when \(x = 64\).

\[\log_{2}{(64)}=6, \quad 1+\log_{4}{(64)}=1+3=4, \quad \text{and} \quad \log_{8}{(4 \cdot 64)} = \log_{8}{(256)}=\dfrac{8}{3}\]

The three terms of the sequence are \(6\), \(4\), \(\dfrac{8}{3}\), which have a common ratio of \(\dfrac{2}{3}\).

Note:
When \(x=\dfrac{1}{4}\), the three terms of the sequence (i.e. \(-2\), \(0\), and \(0\)) have a common ratio of \(0\).

A geometric sequence cannot have a common ratio of \(0\).

Take a moment now to review the key properties of logarithms discussed in this module and summarized here.

Summary

• The logarithmic function, \(y = \log_{c}(x)\), is the inverse of the exponential function, \(y = c^x\), where \(c \gt 0,~c \neq 1\).
• The statement \(\log_{c}(m) = n\) is equivalent to the statement \(m = c^n\).
• The logarithm, \(\log_{c}(x)\), is defined only when \(c \gt 0\), \(c \neq 1\) and \(x \gt 0\).
• A common logarithm is a logarithm base \(10\). When the base is not provided, such as \(\log (x)\), it is assumed to be a common logarithm.
• The following statements hold true for logarithms with \(c \gt 0\) and \(c \neq 1\):
  • \(c^{\log_{c}(n)} = n\), \(n \gt 0\)
  • \(\log_{c}(c^n) = n\)
  • \(\log_{c}(1)=0\)
  • \(\log_{c}(m) = \log_{c}(n)\) if and only if \(m = n\), \(m\) and \(n \gt 0\)
• For \(c \gt 0\), \(c \neq 1\), \(x \gt 0\), \(y \gt 0\),
  • \(\log_{c}(xy)= \log_{c}(x) + \log_{c}(y) \quad\quad\)(Product Law)
  • \(\log_{c}{\left( \frac{x}{y} \right)}= \log_{c}(x) - \log_{c}(y)\quad\;\)(Quotient Law)
  • \(\log_{c}(x^n) = n \log_{c}(x)\quad\quad\quad\quad\quad\;\,\)(Power Law)
• The formula for converting a logarithm from one base to another is \(\log_{c}(x) = \frac{\log_{a}(x)}{\log_{a}(c)}\). This formula is often used to convert to base \(10\).

All of the above properties and laws of logarithms can be used to simplify logarithmic expression and solve exponential and logarithmic equations.